神经网络解释性艺术：理解并解释复杂模型的策略

# 1. 神经网络解释性的基础概念

## 1.1 神经网络解释性的意义

随着人工智能技术的快速发展，神经网络在各个领域的应用变得越来越广泛。然而，伴随而来的是对模型透明度和可解释性的需求不断增长。神经网络解释性指的是理解并阐述神经网络模型做出特定预测或决策的原因和过程。这不仅有助于增强对模型的信任，还能够帮助开发者优化模型结构，提高决策的透明度，并确保符合法律法规和伦理标准。

## 1.2 解释性与模型性能

解释性并非仅仅关乎透明度，它还与模型性能紧密相关。一个可解释的模型有助于识别和纠正模型中的缺陷或偏见，减少过拟合的风险，从而提升模型在现实世界中的泛化能力。例如，通过理解哪些特征对模型预测影响最大，开发者可以调整模型结构或训练数据以改善模型表现。

## 1.3 解释性工具的重要性

为了实现神经网络的解释性，研究人员和工程师已经开发出了多种工具和技术。这些工具从不同的层面揭示了神经网络的行为，如特征的激活模式、输入数据的重要性以及模型内部决策路径等。通过这些工具，非专业人士也能够对复杂的神经网络模型有一个直观的理解，进而辅助决策者做出更明智的选择。

# 2. 理论基础与模型可解释性

## 2.1 神经网络的基本工作原理
### 2.1.1 前馈神经网络与反向传播

在深度学习领域，前馈神经网络是最基本的网络架构之一。在前馈网络中，信息从输入层开始，单向流动至隐藏层，最后到输出层，不存在反馈或环形连接。每个节点仅与前一层的节点相连接，前一层的节点对其输出进行加权求和，再通过激活函数产生非线性变换，从而实现复杂模式的映射和学习。

反向传播算法是训练神经网络的核心机制。通过目标与输出之间的误差计算，该算法能够利用链式法则计算误差对网络权重的影响，并逐步调整权重以减少误差。误差梯度的反向传递是算法名称的由来。为了优化网络的性能，一般采用梯度下降或者其变种算法来对权重进行更新。反向传播使得深度神经网络的训练成为可能，同时也为后文提到的模型可解释性提供了一定的理论基础。

# 伪代码示例：简化的神经网络前向传播和反向传播过程

# 假设有一个简单的三层前馈神经网络
# 输入层为x，隐藏层为h，输出层为y

# 前向传播
h = sigmoid(np.dot(x, W1) + b1) # 隐藏层的加权和以及激活
y = sigmoid(np.dot(h, W2) + b2) # 输出层的加权和以及激活

# 反向传播
error = y - target # 计算输出误差
d_y = error * sigmoid_derivative(y) # 输出误差关于输出层的导数
d_h = d_y.dot(W2.T) * sigmoid_derivative(h) # 误差对隐藏层的影响

# 更新权重和偏置
W2 -= learning_rate * h.T.dot(d_y) # 输出层权重更新
b2 -= learning_rate * np.sum(d_y, axis=0) # 输出层偏置更新
W1 -= learning_rate * x.T.dot(d_h) # 隐藏层权重更新
b1 -= learning_rate * np.sum(d_h, axis=0) # 隐藏层偏置更新

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(x):
    return x * (1 - x)

### 2.1.2 深度学习模型的层次结构

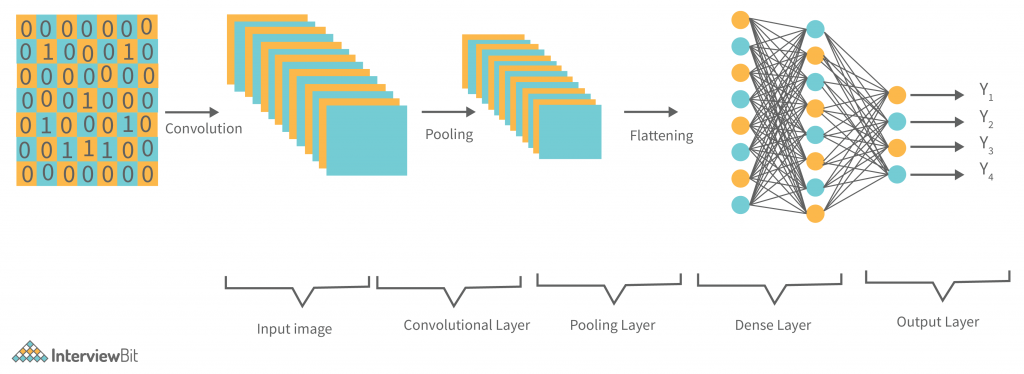
深度学习模型的层次结构使得其能够捕捉数据中的复杂模式和特征。基本层次结构包括输入层、隐藏层（可以有一个或多个）以及输出层。每个隐藏层都由多个神经元组成，而每个神经元负责处理前一层的数据，并将其传递给下一层。随着层次的加深，网络能够学习到从低层次的特征（如边缘和纹理）到更高层次的抽象特征（如物体部件和场景）的表示。

层次化的设计让深度学习模型在图像识别、自然语言处理以及游戏人工智能等领域取得了突破性的进展。模型的深度不仅指网络中隐藏层的个数，也反映了其表示能力的复杂性。然而，这种复杂性也让深度学习模型的决策过程变得难以理解，这正是模型可解释性成为必要讨论话题的原因。

## 2.2 神经网络可解释性的必要性
### 2.2.1 透明度与信任的重要性

在应用深度学习模型时，尤其是涉及到重大决策领域（如医疗诊断、金融信贷和司法判决等），透明度和可解释性显得尤为重要。透明度指的是模型的输入、输出以及内部工作机制对使用者来说是清晰和易于理解的。当模型的预测结果影响到人们的生活时，用户和监管机构会对模型的决策过程提出疑问。通过增加模型的透明度，可以建立用户对模型的信任，这是提升模型可接受度的关键。

信任的确立可以分为多个层次。从最基本的层面看，用户需要相信模型的结果是准确和可靠的。进一步地，用户可能希望理解模型是如何做出这个决策的，例如通过访问模型的关键特征和决策规则。在某些敏感和高风险的应用中，甚至需要对模型的预测进行事后验证和解释。

### 2.2.2 法规与道德考量

在法规层面，欧盟的一般数据保护条例（GDPR）中明确了“被遗忘权”和“解释权”，要求算法的决策过程对个人透明，特别是当算法的输出可能对个人有重大影响时。这要求组织能解释其算法是如何做出特定决策的，以及这些决策如何影响了个人。因此，可解释的算法对于组织来说不仅是一个技术问题，也是一个法律和合规问题。

从道德角度讲，让模型的决策过程透明可以帮助识别和纠正潜在的偏见和歧视。如果一个模型学习到了带有偏见的数据，并且这种偏见没有被检测和纠正，它可能会在决策过程中放大这些偏见，导致不公正的结果。因此，可解释模型有助于促进公平性和道德责任，这对于社会的长期健康发展是必要的。

## 2.3 提高模型可解释性的理论方法
### 2.3.1 局部解释与全局解释

在可解释性理论中，局部解释和全局解释是两种主要的方法。

局部解释关注的是模型在特定决策上的解释能力。也就是说，局部解释尝试回答这样的问题：“为什么模型对于特定的输入给出了这样的预测？”局部解释方法包括但不限于LIME（局部可解释模型-不可解释模型解释器）和SHAP（Shapley Additive exPlanations）值。这些方法试图捕捉模型在局部决策边界附近的行为，给出模型决策的理由。

全局解释则试图提供模型整体行为的解释，而不是单个预测。这包括理解模型中各个特征的重要性和模型如何整体处理信息。全局解释关注的是模型的总体决策模式，包括权重、特征重要性排序等。

# SHAP值的计算实例

import shap
explainer = shap.DeepExplainer(model, X_train)
shap_values = explainer.shap_values(X_test)

# SHAP值结果可视化
shap.summary_plot(shap_values[0], X_test)

### 2.3.2 模型简化与特征重要性评估

除了局部和全局解释方法，简化模型也是提高模型可解释性的一种常见方法。简化模型，如决策树和逻辑回归，通常比复杂的深度学习模型更容易理解和解释。通过简化模型，研究者可以了解哪些特征是重要的，以及这些特征是如何组合以形成决策规则的。

特征重要性评估是一种理解特征对模型预测贡献的方法。常见的特征重要性评估方法包括基于模型的评估（例如随机森林的特征重要性）和基于模型无关的评估（例如Permutation Importance和部分依赖图）。这些方法可以帮助研究者识别模型的关键驱动因素，简化模型，并辅助局部和全局解释。

# 特征重要性评估实例

from sklearn.inspection import permutation_importance

# 使用随机森林模型作为例子
model = RandomForestClassifier()
model.fit(X_train, y_train)

# 计算特征重要性
importances = permutation_importance(model, X_test, y_test, n_repeats=10, random_state=42)

# 可视化特征重要性
indices = np.argsort(importances.importances_mean)
plt.barh(range(len(indices)), importances.importances_mean[indices], color='b', align='center')
plt.yticks(range(len(indices)), [feature_names[i] for i in indices])
plt.xlabel('Relative Importance')
plt.title('Feature Importance')
plt.show()

下一章节将探讨在实践中如何应用不同的解释性工具和技术来提升神经网络模型的可解释性。

# 3. 实践中的解释性工具与技术

## 3.1 可视化技术

### 3.1.1 权重与激活映射

可视化权重与激活映射是解释神经网络决策过程的直接方式之一。权重映射可视化了网络中各个神经元的连接强度，可以直观地显示出哪些输入特征对于特定的神经元是重要的。例如，在图像识别任务中，可以将卷积层的权重映射到原始图像的对应位置，揭示模型在识别过程中关注的区域。

import matplotlib.pyplot as plt
import numpy as np

# 假设weight_matrix是一个卷积层的权重矩阵，我们希望将它可视化
def visualize_weight_map(weight_matrix):
    weight_matrix = weight_matrix.reshape((height, width, filters)