【电路分析进阶秘籍】:频率响应与密勒补偿的巧妙结合
发布时间: 2024-12-15 11:16:58 阅读量: 71 订阅数: 28 


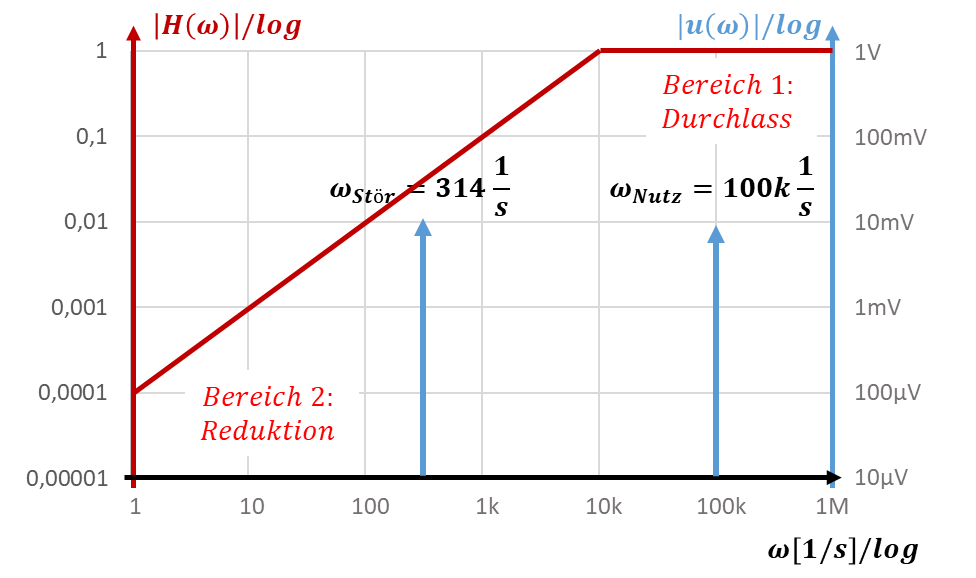
电路中的频率响应,对密勒补偿仿真的分析思考
参考资源链接:[大电容LDO中的Miller补偿:误区与深度解析](https://wenku.csdn.net/doc/1t74pjtw6m?spm=1055.2635.3001.10343)
# 1. 频率响应分析的基础理论
在电子工程领域中,频率响应是指系统对不同频率信号的响应能力,这是评估放大器、滤波器和其他信号处理设备性能的重要参数。理解频率响应的基础理论,对于设计高质量的模拟电路至关重要。本章将介绍频率响应的基本概念,包括幅度响应和相位响应,以及它们对信号完整性的影响。我们将探讨系统函数的构建,它能够描述一个电路对于输入信号频率的增益和相位偏移。通过分析一个系统的频率响应,工程师能够优化电路设计,提高其对特定频率范围信号的处理能力,确保电路在工作频率范围内具有良好的稳定性和精确度。
# 2. 密勒效应与密勒定理
## 2.1 密勒效应的基本概念
### 2.1.1 密勒效应的定义和物理意义
密勒效应是电子学中一个重要的概念,它描述了在特定电路配置下,电容器两端电压变化对输入信号的影响。密勒效应的一个典型应用是在运算放大器的反馈网络中,尤其是当大容量的反馈电容与输入或输出端相连接时。这种效应导致了输入端看到一个放大了的电容值,这个值是实际反馈电容值和增益的乘积。物理上,这种效应是由电子设备中载流子的重新分布引起的。
在电路分析中,密勒效应对于理解电路动态特性至关重要。它影响了电路的频率响应,特别是对放大器的高频响应。密勒效应的存在使电路设计师能够通过特定设计减少所需的元件数量,达到节省成本和电路板空间的目的。
### 2.1.2 密勒定理的数学表达
密勒定理提供了分析密勒效应的数学工具。它允许我们用等效的电容值来代替实际电路中由于密勒效应而产生的更大电容值。数学上,密勒定理可以表示为以下公式:
```
C_miller = (1 - A_v) * C_actual
```
其中 `C_miller` 是等效的密勒电容,`A_v` 是放大器的电压增益,`C_actual` 是实际的物理电容值。从上述公式可以看出,如果放大器的增益非常大,那么等效的密勒电容值将接近于实际电容值的相反数乘以增益的绝对值,这意味着实际上电路中的电容效应被放大了很多倍。
## 2.2 密勒效应在放大器中的应用
### 2.2.1 反馈放大器中的密勒效应分析
在反馈放大器设计中,密勒效应扮演着关键角色。当一个大容量的电容器作为反馈元件跨接在放大器的输入和输出之间时,密勒效应导致输入端看到一个放大了的电容值,这直接影响了放大器的频率响应。这种效应在高速运算放大器设计中尤为重要,因为频率响应直接关系到放大器的带宽和信号完整性。
放大器中的密勒电容对电路性能有着双重影响。一方面,它可以在一定程度上抑制高频信号,避免电路因为高速开关而导致的高频振荡,提高电路的稳定性;另一方面,过大的密勒电容会降低放大器的带宽,限制了电路在高频下的应用能力。
### 2.2.2 密勒效应对放大器频率响应的影响
密勒效应对放大器的频率响应有显著的影响。具体来说,放大器的带宽会受到等效的密勒电容的影响。增加的等效电容值会使得放大器在高频下的增益降低,因此限制了放大器的带宽。
为了优化放大器的频率响应,通常需要采用一些补偿技术来对抗密勒效应的影响。例如,在运算放大器中,设计师可以通过减少反馈电容值或者增加相位补偿电路来减轻密勒效应的影响,使得放大器能够在更宽的频率范围内保持稳定的工作状态。
在放大器设计中,理解并有效管理密勒效应是至关重要的。通过计算和调整反馈网络中的密勒电容值,设计师能够控制放大器的频率响应,并确保电路在设计的目标频率范围内正常工作。这涉及到对电路元件的精确选择和布局,以及对电路动态行为的深入理解。
# 3. 频率响应的深入探究
在理解了频率响应的基础理论和密勒效应后,本章将深入探究频率响应的数学模型以及如何在实践中测量和优化频率响应。这将为工程师们提供更深层次的理解和实际应用的能力,以实现系统性能的最优化。
## 3.1 频率响应的数学模型
### 3.1.1 Bode图和频谱分析
Bode图是分析线性时不变系统频率响应的一种常用工具。它由幅度图和相位图两部分组成,分别描述了系统增益随频率变化的情况和系统相位响应。
- **幅度图**:通常以分贝(dB)为单位,显示了系统增益(或幅度比)随频率的变化。横轴是频率的对数尺度,纵轴是增益。
- **相位图**:显示了系统输出与输入之间的相位差随频率变化的情况。
频谱分析涉及到将信号分解为不同频率成分的过程,通常使用快速傅里叶变换(FFT)算法来实现。通过频谱分析,可以直观地看到信号中各频率成分的强度分布。
### 3.1.2 频率响应函数的求解方法
频率响应函数(Frequency Response Function, FRF)描述了一个线性系统对不同频率输入信号的响应。它可以通过线性系统理论中的传递函数来获得,其中传递函数H(jω)与频率响应函数H(f)的关系为:
\[ H(f) = \left| H(j\omega) \right| \]
\[ \phi(f) = \angle H(j\omega) \]
其中,|H(jω)|表示频率响应函数的幅度,∠H(jω)表示相位。求解FRF通常涉及系统差分方程或微分方程的解析,以及拉普拉斯变换的使用。
## 3.2 频率响应的实践测量
### 3.2.1 实验设置和测量技术
在实践中,测量频率响应通常需要使用网络分析仪。该设备能够发送特定频率的信号,并测量系统对这些信号的响应。
**实验设置包括以下步骤:**
1. 准备网络分析仪和待测系统。
2. 将网络分析仪连接到系统输入和输出端。
3. 进行系统校准,以消除测试仪器引入的误差。
4. 对系统进行扫频,记录不同频率下的增益和相位响应。
5. 分析所得数据,确定系统频率响应特性。
### 3.2.2 数据解读与频率补偿的必要性
通过实验测量获得的频率响应数据需要被解读,以确定系统是否满足设计要求。解读过程包括对幅度和相位的评估,以及寻找可能存在的共振峰或衰减区域。根据测量结果,可能需要进行频率补偿来改善系统性能。
**频率补偿的必要性体现在以下几个方面:**
1. 提高稳定性:通过补偿来避免系统的不稳定行为,如振荡。
2. 增强性能:通过调整频率特性来改善系统对特定信号的响应。
3. 扩展带宽:使得系统能够有效地处理更宽频率范围内的信号。
**频率补偿的实施方法:**
1. 设计适当的补偿网络,如使用电容器或电感器来调整频率响应。
2. 利用数字信号处理技术进行补偿,如滤波器设计。
3. 在反馈回路中引入补偿,以改变闭环系统的频率响应。
频率响应的深入探究不仅限于理论分析,更关键的是通过实验测量和补偿策略来实现最佳的系统性能。以下是一个使用电路仿真软件进行频率响应模拟的实例代码块:
```python
import matplotlib.pyplot as plt
from scipy.signal import lti, bode
import numpy as np
# 定义系统传递函数
numerator = [1] #
```
0
0





