Cairo图形变换高级技巧：曲线与非线性变换的艺术

# 1. Cairo图形库概述

## 1.1 Cairo图形库简介
Cairo是一个开源的2D图形库，它提供了一套丰富的API，使得开发者能够在各种不同的输出设备上绘制矢量图形。Cairo的应用广泛，从简单的图形绘制到复杂的动画制作，都可以通过它来实现。

## 1.2 Cairo的核心特性
Cairo的核心特性包括跨平台、硬件加速、支持多种输出格式等。它不仅可以运行在Linux系统上，还可以在Windows、Mac OS X等操作系统上运行。Cairo还支持多种后端，如PDF、SVG、PostScript等，使得图形输出更加多样化。

## 1.3 Cairo的使用场景
Cairo非常适合用于创建图形用户界面(GUI)、Web图形和图形应用程序。它的高性能和灵活性使得它成为许多软件开发者的首选图形库。在接下来的章节中，我们将深入探讨Cairo图形库在曲线变换方面的应用和技巧。

# 2. 曲线变换的艺术

### 2.1 曲线变换的基本概念

#### 2.1.1 曲线变换的定义和重要性
在计算机图形学中，曲线变换是一种基本的图形操作技术，它涉及将一组控制点映射到另一组控制点，从而改变曲线的形状和方向。这种技术在动画、图形设计、用户界面设计等领域都有广泛的应用。

曲线变换的重要性体现在以下几个方面：

1. **图形设计**：通过曲线变换，设计师可以创造出复杂而优雅的图形形状，增强视觉效果。
2. **动画制作**：在动画中，曲线变换用于实现平滑的运动和过渡效果，提供更自然的视觉体验。
3. **用户界面**：曲线变换可以用于改善用户界面元素的交互体验，如平滑滚动、动态反馈等。

#### 2.1.2 曲线变换与线性变换的对比
曲线变换与线性变换的主要区别在于它们是否能够改变曲线的形状。线性变换，如旋转、缩放和平移，只能对曲线进行刚性移动，不会改变其形状。而曲线变换则可以改变曲线的形状和方向，实现更为复杂的效果。

### 2.2 曲线变换的实现方法

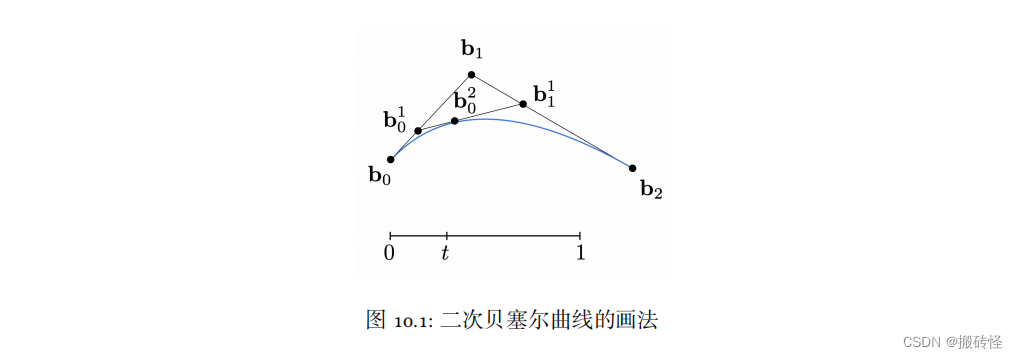
#### 2.2.1 使用贝塞尔曲线进行变换
贝塞尔曲线是一种广泛使用的参数曲线，它通过控制点定义曲线的形状。贝塞尔曲线变换通常涉及以下步骤：

1. **定义控制点**：首先定义原始曲线的控制点。
2. **计算曲线方程**：根据控制点计算贝塞尔曲线的数学方程。
3. **变换控制点**：应用变换矩阵到控制点，改变曲线的位置和形状。
4. **重新绘制曲线**：使用新的控制点绘制变换后的贝塞尔曲线。

# Python示例代码：使用贝塞尔曲线进行变换
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import PathPatch
from matplotlib.path import Path

# 定义贝塞尔曲线的控制点
bezier_points = np.array([[0, 0], [0.5, 1], [1, 0], [1, 1]])

# 计算贝塞尔曲线路径
bezier_path = Path(bezier_points)
bezier_patch = PathPatch(bezier_path, facecolor="none", lw=2)

# 创建图形和坐标轴
fig, ax = plt.subplots()
ax.add_patch(bezier_patch)

# 设置坐标轴范围
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)

# 显示图形
plt.show()

#### 2.2.2 通过样条曲线实现复杂图形
样条曲线是一种通过一系列控制点定义的平滑曲线，它比贝塞尔曲线更灵活，能够创建更加复杂的曲线形状。样条曲线变换涉及以下步骤：

1. **定义控制点**：定义原始曲线的控制点。
2. **计算样条曲线方程**：根据控制点计算样条曲线的数学方程。
3. **变换控制点**：应用变换矩阵到控制点，改变曲线的位置和形状。
4. **重新绘制曲线**：使用新的控制点绘制变换后的样条曲线。

### 2.3 曲线变换的优化技巧

#### 2.3.1 提高曲线渲染性能的方法
为了提高曲线渲染性能，可以采取以下优化方法：

1. **预计算变换**：对于静态曲线，提前计算变换后的控制点，避免实时计算。
2. **分段绘制**：将复杂曲线分解为多个简单曲线段，分别绘制，提高渲染效率。
3. **使用GPU加速**：利用图形处理单元（GPU）进行曲线渲染，提高处理速度。

#### 2.3.2 曲线变换的抗锯齿处理
曲线变换可能导致渲染输出中的锯齿现象。为了减少锯齿，可以采用以下抗锯齿技术：

1. **多重采样**：在曲线周围采样多个点，并计算平均颜色值，以平滑边缘。
2. **后处理滤镜**：应用滤镜技术，如高斯模糊，以平滑曲线边缘。
3. **子像素渲染**：利用子像素的精度进行渲染，提高曲线边缘的平滑度。

# Python示例代码：抗锯齿处理
import numpy as np
import matplotlib.pyplot as plt
from scipy.ndimage import gaussian_filter

# 定义曲线函数
def curve_function(x):
    return np.sin(x) * np.exp(-x/3)

# 生成曲线上的点
x = np.linspace(0, 10, 1000)
y = curve_function(x)

# 应用多重采样抗锯齿
sampled_y = np.array([np.mean(curve_function(x[i:i+10])) for i in range(0, len(x), 10)])

# 应用高斯模糊抗锯齿
smoothed_y = gaussian_filter(y, sigma=0.5)

# 绘制原始曲线和抗锯齿处理后的曲线
plt.plot(x, y, label='Original Curve')
plt.plot(x, sampled_y, label='Multi-sampled Antialiasing')
plt.plot(x, smoothed_y, label='Gaussian Blur Antialiasing')

plt.legend()
plt.show()

通过本章节的介绍，我们了解了曲线变换的基本概念、实现方法以及优化技巧。曲线变换不仅能够帮助我们创建复杂的图形，还能够在动画和图形设计中实现平滑和优雅的效果。在下一章节中，我们将探讨非线性变换的基本原理及其在图形学中的应用。

# 3. 非线性变换的实践应用

## 3.1 非线性变换的基本原理

### 3.1.1 非线性变换的定义和分类

非线性变换是图形学中的一个重要概念，它描述了在图形变换过程中，输出与输入之间不是线性关系的现象。与线性变换相比，非线性变换能够提供更丰富的视觉效果，如透视感、弹性变形等。在数学上，非线性变换通常指的是输入和输出之间的关系不能用线性方程描述的变换。

非线性变换的分类主要基于其数学性质和应用场景。常见的非线性变换包括但不限于：