【湍流模型与非定常流动】：理论到数值模拟的桥梁


# 摘要
本文全面探讨了湍流模型与非定常流动的基础理论及其数值模拟技术。从湍流的定义、分类到其统计理论基础，本文深入解析了湍流模型的分类原理，并对非定常流动的特点及其数值模拟方法进行了详尽分析。接着，文章介绍了数值模拟的基本方法，包括离散化技术、差分方法以及网格生成与优化技术，还探讨了湍流模型在计算流体动力学软件中的数值实现和边界条件处理。通过瞬态流动的数值解法、频域分析在非定常流动中的应用以及湍流模拟的后处理技术，本文在模拟实践层面提供了深刻见解。高级湍流模型如大涡模拟(LES)和直接数值模拟(DNS)的介绍，以及复杂流场的模拟策略和工程应用案例分析，进一步拓展了本文的应用视野。最后，本文对湍流模型的未来趋势、挑战和前沿问题进行了展望，强调了机器学习、人工智能和高性能计算在湍流模拟中的重要作用，以及在环境与生物医学领域内湍流研究的必要性。

# 关键字
湍流模型；非定常流动；数值模拟；计算流体动力学；网格生成；大涡模拟

参考资源链接：[FLUENT非定常流动分析详解：时间步设置与计算技巧](https://wenku.csdn.net/doc/itgrwd7jsd?spm=1055.2635.3001.10343)
# 1. 湍流模型与非定常流动基础

## 1.1 湍流的基本概念

湍流是流体力学中一种极为复杂的现象，涉及流体速度、压力和温度等参数的快速和不规则变化。它在自然环境和工程应用中无处不在，例如大气流动、河流的流动、航空航天器的飞行以及工业中的管道流动等。理解湍流的特性是进行有效数值模拟和实验研究的基础。

## 1.2 湍流的分类与特性

湍流的分类通常依据Reynolds数（雷诺数），它是一个无量纲参数，用于描述流体流动状态。当雷诺数较小（<2000）时，流动表现为层流，流体运动平滑有序；当雷诺数增大，流动逐渐过渡到湍流状态，流场表现出高度不规则的运动特征。

## 1.3 非定常流动的定义

非定常流动指的是随时间变化的流动状态，区别于稳定不变的定常流动。在非定常流动中，流体的参数如速度、压力、温度等可能随时间或空间位置发生变化，从而使得流动分析变得更加复杂。非定常流动是研究湍流现象不可或缺的一部分。

graph TD;
    A[湍流基本概念] --> B[湍流分类与特性]
    B --> C[层流]
    B --> D[过渡流]
    B --> E[湍流]
    A --> F[非定常流动]
    F --> G[时间变化特性]
    F --> H[空间变化特性]

在本章中，我们将深入探讨湍流与非定常流动的基本概念、特性及其重要性，为后续章节中更为高级的数值模拟技术与应用案例打下坚实的基础。

# 2. ```
# 第二章：湍流模型的理论框架

在探索湍流这一复杂现象的奥秘时，理论框架的建立是不可或缺的一步。本章将深入探讨湍流模型的理论基础，分析湍流的基本特性和湍流模型的分类原理，进而分析非定常流动现象，从而为后续章节的数值模拟技术与实践操作打下坚实的理论基础。

## 2.1 湍流的基本特性

湍流是流体动力学领域内一种高度非线性的复杂现象。在这一部分，我们首先介绍湍流的定义和分类，并深入探讨湍流的统计理论基础。

### 2.1.1 湍流的定义与分类

湍流是一种在流体中形成的无规则、剧烈的流动状态，与之相对的是层流，即一种有序、平滑的流动状态。湍流中的流体运动呈现出高度的随机性，涉及多种尺度的涡旋。这种无序状态的流体运动使得湍流的直接解析变得异常复杂。

按Reynolds数划分，湍流可以分为完全湍流和过渡湍流。Reynolds数是惯性力与粘性力的比值，它在流体力学中起着至关重要的作用。低Reynolds数的流动通常呈现为层流，而高Reynolds数则可能导致完全湍流。

### 2.1.2 湍流的统计理论基础

湍流的统计理论是通过概率统计方法对湍流特性进行描述的基础。这种方法基于对流体速度场的统计分析，能够提供平均流动特性及脉动量的统计信息。湍流的统计理论包括基本统计量（如均值、方差）和相关函数，通过这些统计量，可以构建湍流脉动的统计模型。

## 2.2 湍流模型的分类与原理

湍流模型是用来模拟湍流特性的数学模型，通过不同层次的近似和简化，这些模型能够帮助我们预测实际湍流流动的特性。本节将对零方程模型、一方程模型、二方程模型这三类常见的湍流模型进行分类与原理分析。

### 2.2.1 零方程模型

零方程模型是最简单的湍流模型，它不需要求解湍流动能方程，直接通过代数关系表达流速和应力之间的关系。这类模型通常在粘性影响较大的流动区域比较有效，比如边界层附近的流动。

### 2.2.2 一方程模型

一方程模型相比零方程模型进一步考虑了湍流能量的传输，需要求解一个关于湍流动能的方程。虽然模型复杂度增加，但能给出比零方程模型更为准确的预测，尤其在预测自由剪切层流动时。

### 2.2.3 二方程模型

二方程模型是目前工程应用中最常用的湍流模型之一。在这种模型中，通过引入湍流动能和湍流耗散率两个方程来描述湍流特性。由于其更细致地考虑了湍流的动态特性，二方程模型可以用来模拟更复杂的湍流流动。

## 2.3 非定常流动现象分析

在非定常流动中，流动参数不仅随空间位置变化，而且还随时间变化。本节将着重分析非定常流动的特点以及数值模拟方法。

### 2.3.1 非定常流动的特点

非定常流动的特点是其流动参数随时间变化。这种流动特性是由于流动中的扰动或外加力作用导致的，如风洞测试中的振荡翼型或发动机启动过程中的流动变化。

### 2.3.2 非定常流动的数值模拟方法

非定常流动的数值模拟方法主要包括时间积分方法和时间步长的选择。时间积分方法如显式方法和隐式方法各有优势。显式方法计算简单，但稳定性较差；隐式方法稳定性好，但计算量较大。时间步长的选择需要综合考虑计算的稳定性和准确性。

以上内容为第二章内容的概要介绍，由于篇幅限制，实际文章中应进一步详细展开各小节内容。此外，为了进一步增强文章的深度和连贯性，应当在小节内加入实际案例、操作步骤、代码块、逻辑分析、参数说明以及相关的图表与流程图。在各章节的结合处，也应当有适当的文字过渡，以确保文章读起来流畅自然。

# 3. 数值模拟技术与计算方法

## 3.1 数值模拟的基本方法

### 3.1.1 离散化技术

数值模拟的核心在于将连续的物理过程转换为离散的数学模型，这一过程被称为离散化。离散化技术的选择直接影响到模拟的准确度和效率。常见的离散化技术包括有限差分法、有限元法和有限体积法。

有限差分法是通过对控制方程中的偏导数进行差分近似，从而在空间网格上建立代数方程组。有限元法则侧重于将整个求解区域划分为多个小的、简单的单元，在每个单元上求解局部问题，再通过全局组装得到整个区域的解。有限体积法则是基于守恒定律，通过对控制体内的物理量进行积分来建立代数方程组。

对于湍流模型而言，不同的离散化技术会有不同的数值特性，如耗散性、色散性等。在实际应用中，需要根据具体问题和求解器的特性来选择合适的离散化方法。

### 3.1.2 差分方法与有限体积法

差分方法是将偏微分方程离散为一组代数方程的方法，其核心在于使用有限差分公式来近似微分算子。例如，一阶导数可以使用前向差分、后向差分或中心差分进行近似。

有限体积法则是将连续的控制方程转换为对离散控制体积积分的形式。通过积分形式的守恒定律，可以确保物理量的守恒性，这对于流体动力学问题尤为重要。

有限体积法是计算流体动力学（CFD）中常用的方法之一。它对边界条件处理方便，计算效率较高，同时保持了较好的计算稳定性。在实际应用中，通过选择合适的差分格式（例如迎风格式、中心格式等）和网格类型，可以在计算精度和稳定性之间取得平衡。

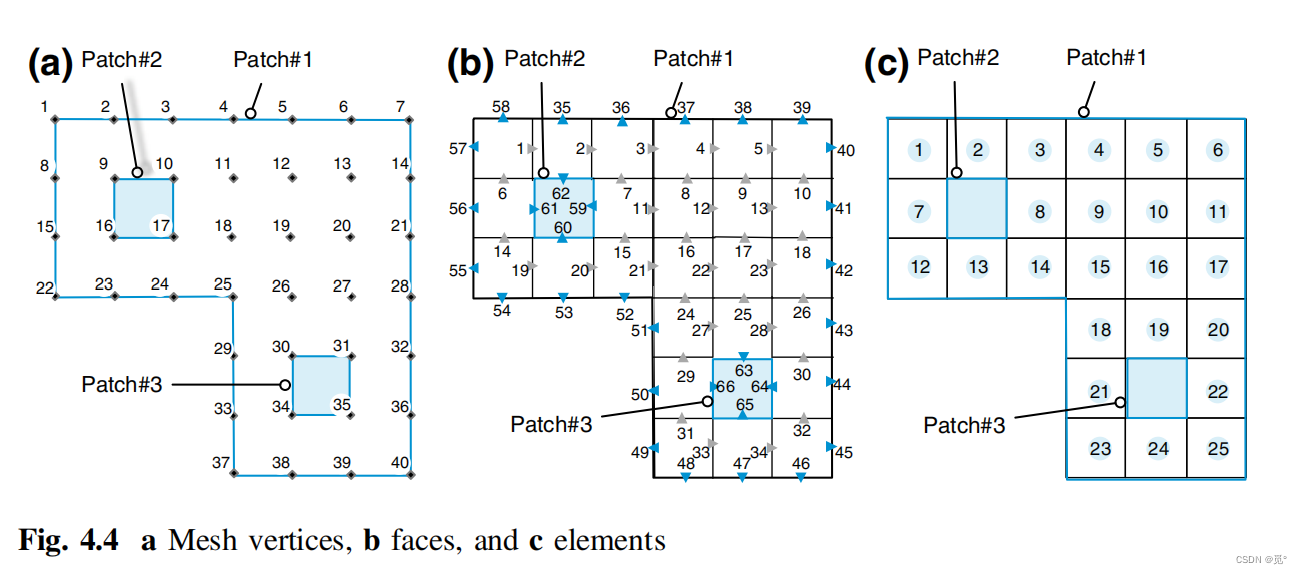
## 3.2 网格生成与优化技术

### 3.2.1 结构化网格与非结构化网格