【并发数据安全】：并发环境下数据结构的线程安全增长机制

# 1. 并发数据安全的基本概念

在现代软件开发中，尤其是构建高并发系统时，数据安全和线程安全是两个不可忽视的话题。理解并发数据安全的基本概念，为深入探讨线程安全打下坚实的基础。本章将从并发、数据安全和线程安全的基本定义出发，深入浅出地探讨它们之间的关系以及在软件开发中的重要性。

## 1.1 并发编程的背景

在多核处理器普及的今天，利用并发编程技术来提高程序性能已成为开发者的必备技能。并发编程使得多个计算任务能够同时执行，从而有效利用硬件资源，缩短程序运行时间。然而，伴随着并发操作的增多，数据安全问题也日益凸显。

## 1.2 数据安全的含义

数据安全主要指在并发环境下，确保数据的完整性、准确性和一致性。不同的应用场景对数据安全有着不同的要求，比如金融系统需要严格的数据一致性，而一些实时分析系统可能对数据一致性有稍许的妥协以换取高吞吐量。

## 1.3 线程安全的重要性

线程安全是并发编程中数据安全的一个子集，它确保了在多线程环境下，共享资源的访问不会导致意外的结果。线程安全问题直接关系到程序的稳定性和可靠性，是软件质量的关键所在。

总结起来，本章通过阐述并发编程的背景、数据安全和线程安全的含义，为读者构建起一个全面的并发数据安全的知识框架。在后续章节中，我们将深入分析线程安全的基础理论和相关的技术细节，进一步探索如何在实际编程中实现和优化线程安全。

# 2. 线程安全的基础理论

## 2.1 线程安全的定义和重要性

线程安全是指在多线程环境中，一段代码或者程序执行时能够正确处理多个线程间共享资源访问的问题，确保数据的一致性和完整性。该定义对任何涉及多线程编程的语言和平台都至关重要，是构建可靠并发应用程序的基础。

### 2.1.1 线程安全与数据一致性

在多线程程序中，多个线程可能会同时访问和修改同一数据资源，这会导致数据竞争和不一致的问题。线程安全的关注点在于，即使在多线程同时操作的情况下，也能够保证数据的一致性。

**数据一致性的实现方式：**

- **互斥访问**：利用锁机制保证同一时间只有一个线程可以访问特定数据。
- **不可变对象**：创建不可被改变的对象，从而避免数据不一致的问题。
- **局部变量**：使用局部变量来避免多线程间的共享。
- **并发控制**：使用事务控制或者版本控制等机制来保证操作的原子性。

### 2.1.2 并发与数据安全的关系

并发是多线程编程的核心概念，它涉及在程序运行时同时执行多个操作的能力。正确的并发控制对于数据安全至关重要。

**并发数据安全的关键要素：**

- **原子操作**：确保并发环境下某个操作的执行不可中断。
- **锁机制**：控制对共享资源的访问，防止数据竞争。
- **内存顺序**：确保内存访问的顺序性，避免读写操作的重排。

## 2.2 线程同步机制基础

同步机制是实现线程安全的核心手段，它通过协调多线程之间的执行顺序，保证数据操作的正确性。

### 2.2.1 互斥锁与条件变量

互斥锁（Mutex）和条件变量（Condition Variable）是常用的同步工具。

**互斥锁的作用：**

- 确保同一时间只有一个线程能访问临界区。
- 防止数据竞争。

**条件变量的作用：**

- 在某些条件下阻塞线程，直到其他线程通知条件满足。

#include <mutex>
#include <condition_variable>

std::mutex mtx;
std::condition_variable cv;

void waiting_for_a_signal() {
    std::unique_lock<std::mutex> lock(mtx);
    cv.wait(lock, []{ return shared_data_ready; });
    // 处理共享数据
}

void signal_when_data_ready() {
    std::lock_guard<std::mutex> lock(mtx);
    shared_data_ready = true;
    cv.notify_one();
}

**参数说明和逻辑分析：**

- `std::mutex` 用于创建互斥锁。
- `std::condition_variable` 用于创建条件变量。
- `std::unique_lock` 和 `std::lock_guard` 用于管理锁的生命周期。

### 2.2.2 信号量和自旋锁

信号量（Semaphore）和自旋锁（Spinlock）是线程同步的另一种机制，它们在不同的场景下有不同的应用。

**信号量特点：**

- 能够允许多个线程访问共享资源。
- 可用于限制对资源的最大访问数量。

**自旋锁特点：**

- 当锁不可用时，线程会持续检查锁的状态直到锁可用。
- 适用于锁持有时间短的场景。

### 2.2.3 原子操作与内存屏障

原子操作保证操作的不可分割性，内存屏障则用于保证内存操作的顺序性。

**原子操作示例：**

#include <atomic>

std::atomic<int> counter(0);

void increment() {
    counter.fetch_add(1, std::memory_order_relaxed);
}

int get_count() {
    return counter.load(std::memory_order_relaxed);
}

**参数说明和逻辑分析：**

- `std::atomic` 用于创建原子类型。
- `fetch_add` 和 `load` 是原子操作，保证了整数的增减和读取的原子性。

**内存屏障的作用：**

- 防止编译器、处理器指令的重排。
- 确保代码中指定的内存访问顺序。

## 2.3 错误处理与死锁预防

错误处理和死锁预防是确保线程安全的辅助手段，它们能够减少程序运行时的不确定性和不稳定性。

### 2.3.1 死锁的产生条件与预防策略

死锁是多线程编程中经常遇到的问题，它发生在多个线程相互等待对方释放资源，从而导致程序挂起。

**死锁产生的四个必要条件：**

- 互斥条件：资源不能被共享，只能由一个线程使用。
- 占有和等待条件：线程至少持有一个资源，并且正在等待获取其他线程占有的资源。
- 不可剥夺条件：线程已获得的资源，在未使用完之前，不能被其他线程强行夺走，只能由占有资源的线程自愿释放。
- 循环等待条件：存在一种线程资源的循环等待关系。

**预防死锁的策略：**

- **资源分配顺序**：定义所有资源的线性分配顺序，避免循环等待。
- **一次性分配**：要求线程在开始执行前一次性请求所有需要的资源。
- **资源抢占**：当资源被占用且不能满足某个线程请求时，抢占已占有的资源。

### 2.3.2 错误处理机制和日志记录

错误处理机制可以确保在出现异常情况时，程序能够安全地处理，并能够通过日志记录来追踪问题。

**错误处理的要点：**

- **异常捕获**：使用 try-catch 块捕获并处理可能发生的异常。
- **资源释放**：确保在异常发生时释放已占有的资源。
- **日志记录**：详细记录程序运行期间的异常信息和关键数据，便于调试和分析问题原因。

本章节介绍了线程安全的基础理论，深入探讨了线程安全的定义、重要性、同步机制、死锁预防以及错误处理机制，为后续章节中并发数据结构设计与实现、性能优化和实践案例奠定了理论基础。在实际开发中，开发者应当充分理解并应用这些理论，确保应用程序的线程安全和高效并发执行。

# 3. 并发数据结构的设计与实现

## 3.1 线程安全的数据结构类型
### 3.1.1 锁分离与锁粒度控制

在并发编程中，锁是一种重要的同步手段，用于控制对共享资源的访问，以保证数据的一致性和完整性。随着并发级别和需求的增长，锁的使用策略也需要相应地进行优化。锁分离和锁粒度控制就是两种常见的优化策略。

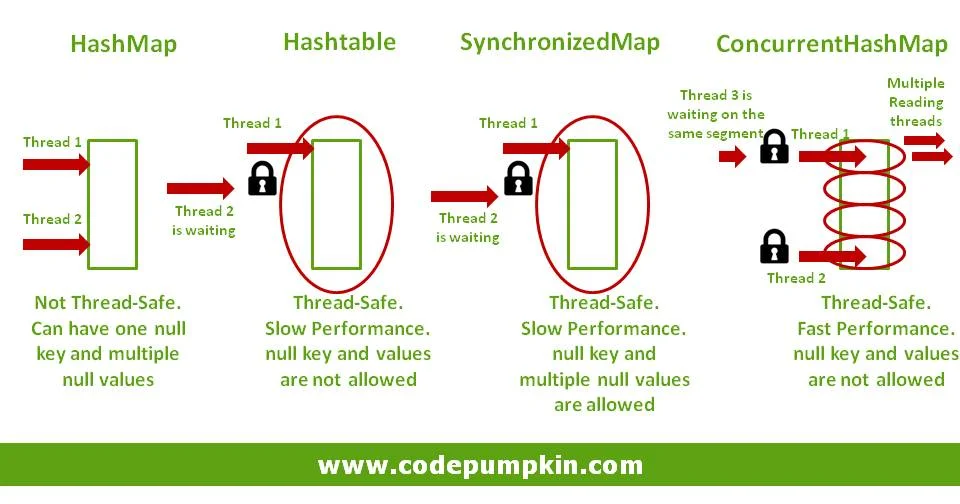
锁分离是指将一个复杂的锁定操作分解为多个更小、更具体的锁定操作。这种方法可以提高并发性能，因为它允许不同的线程在不冲突的情况下同时访问数据的不同部分。例如，`ConcurrentHashMap`在Java中就是通过分离锁来实现的，它将数据分成多个段（segment），每个段有自己的锁。这样，读取操作往往不需要全局锁，从而显著提高了并发性能。

锁粒度控制则关注如何恰当地调整锁的范围，以减少不必要的锁定时间。在实践中，可以将锁的粒度设置为细粒度以获得更高的并发度，或者设置为粗粒度以降低系统开销。例如，在某些数据库系统中，可以实现行级锁或表级锁，根据操作的类型选择最合适的锁定级别。

以下是Java代码示例，展示了如何在集合类中应用锁分离策略：

public class SegmentMap<K, V> {
    // 每个segment单独持有锁
    private final Segment<K, V>[] segments;

    public SegmentMap(int numSegments) {
        segments = new Segment[numSegments];
        for (int i = 0; i < numSegments; ++i)
            segments[i] = new Segment<>();
    }

    private static class Segment<K, V> {
        private final HashMap<K, V> map = new HashMap<>();

        // 锁对象控制对segment的访问
        private final Object lock = new Object();

        V get(Object key, int hash) {
            synchronized (lock) {
                return map.get(key);
            }
        }

        V put(K key, V value, int hash) {
            synchronized (lock) {
                return map.put(key, value);
            }
        }
    }
}

在上述代码中，`SegmentMap`类通过使用多个`Segment`对象实现锁分离。每个`Segment`负责一部分数据，并且拥有自己的锁对象。当需要访问数据时，只锁定涉及的那个`Segment`，而不是整个`SegmentMap`。

### 3.1.2 无锁数据结构的概念与应用

无锁数据结构通过使用原子操作来替代传统锁机制，在减少锁的开销的同时，提高并发效率。原子操作是一种在执行过程中不会