【SEGY-SeiSee时间序列深度解析】：挖掘地震数据时间特征的专家指南


参考资源链接：[SeiSee：SEG-Y地震数据处理与分析指南](https://wenku.csdn.net/doc/6412b54dbe7fbd1778d42a96?spm=1055.2635.3001.10343)
# 1. SEGY文件格式与地震数据基础

地震数据是地球物理学研究中的宝贵资料，它们为我们提供了有关地壳内部结构和动力学过程的直接信息。SEGY（Standard for the Exchange of Geophysical Data）是一种广泛应用于地震数据存储和交换的文件格式。本章将带领读者了解SEGY文件的基础知识和地震数据的基本概念。

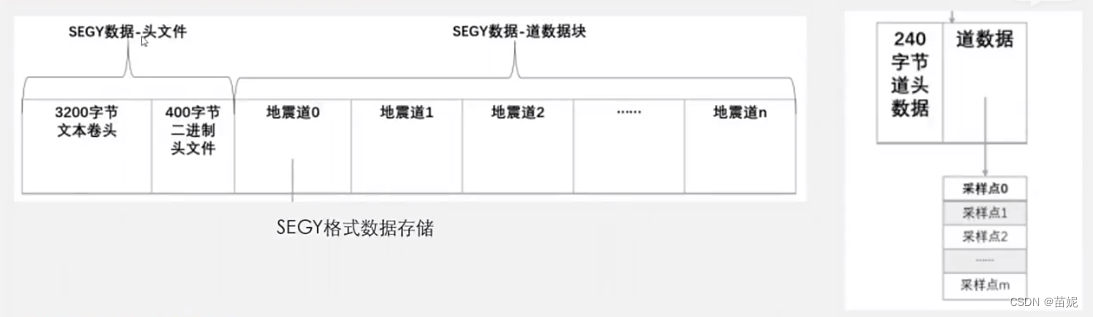
SEGY文件格式是地震数据处理领域的标准格式之一，它的设计允许地球物理学家共享和分析不同来源的数据。SEGY文件中存储了地震波的振幅数据以及相关的头文件信息，其中头文件包含了采集时间、地理位置、仪器参数等重要信息。理解SEGY格式的结构对于地震数据的导入、处理和解释至关重要。

地震数据通常包括一系列随时间变化的地震波形记录，它们反映了地震波通过不同地质结构的传播特性。地震数据的分析可揭露地下构造的信息，为油气勘探、地震风险评估等领域提供支持。本章内容将为深入学习后续章节的时间序列分析与数据处理奠定基础。

# 2. 时间序列分析基础与SEGY数据处理

## 2.1 时间序列分析理论

### 2.1.1 时间序列的概念与特征

时间序列是由同一变量在不同时间点上所观测到的有序数据集合，每个数据点都是随时间连续采样的结果。在地震学中，时间序列通常代表地震波形数据在时间轴上的变化。这些数据具有以下特征：

- 时间连续性：观测值是按时间顺序连续记录的。
- 等间隔性：通常假设每个时间点上的观测是等时间间隔的。
- 多样性：时间序列可以是单变量的，也可以是多变量的（多元时间序列），在地震学中通常是多变量的。

时间序列分析的目的在于从数据中提取有价值的信息，比如趋势、周期性、季节性变化等，用以理解和预测未来的变化。

### 2.1.2 常见的时间序列模型和方法

时间序列分析的方法多种多样，常见的模型和方法包括：

- 自回归模型（AR）：模型中的当前值由其前n个值的线性组合加上一个随机误差项组成。
- 移动平均模型（MA）：当前值依赖于历史观测值和随机误差项的线性组合。
- 自回归移动平均模型（ARMA）：是AR和MA的结合，用以描述时间序列数据中的趋势和周期性。
- 自回归积分滑动平均模型（ARIMA）：适用于非平稳时间序列的数据，通过差分将非平稳序列转化为平稳序列，再应用ARMA模型。
- 季节性自回归移动平均模型（SARIMA）：是ARIMA模型的扩展，考虑时间序列的季节性变化。

## 2.2 SEGY数据的预处理

### 2.2.1 数据导入与格式转换

SEGY（Standard for the Exchange of Geophysical Data）是一种广泛使用的地震数据交换格式。SEGY文件通常包含地震波形数据、头文件信息、采样率等重要数据。为了进行时间序列分析，必须先将SEGY数据导入到分析软件中，并进行必要的格式转换。

以Python中的`obspy`库为例，以下是一个导入SEGY文件并进行格式转换的代码示例：

from obspy import read

# 读取SEGY文件
st = read("/path/to/your/seg_y_file.segy")

# 进行格式转换，假设我们需要将数据转换为MiniSEED格式
st.write("/path/to/output/mini_seed_file.mseed", format="MSEED")

执行上述代码后，SEGY文件中的数据就被导入到内存中，并转换为其他格式。

### 2.2.2 噪声过滤与数据清洗

噪声和非地震信号的干扰在地震数据中普遍存在，为了提高分析的准确度，必须进行噪声过滤和数据清洗。常见的噪声类型包括随机噪声、系统噪声、地面噪声等。常用的方法有：

- 带通滤波器：允许特定频率范围内的信号通过，过滤掉高频和低频噪声。
- 基于统计的去噪技术：利用统计方法，比如中值滤波，识别并去除异常值。

以Python中的`scipy`库为例，以下是一个应用带通滤波器进行噪声过滤的代码示例：

import numpy as np
from scipy.signal import butter, lfilter

# 设定带通滤波器的频率范围
lowcut = 1.0
highcut = 30.0
nyq = 0.5 * sampling_rate  # 奈奎斯特频率
low = lowcut / nyq
high = highcut / nyq

# 设计Butterworth滤波器
def butter_bandpass(lowcut, highcut, fs, order=5):
    nyq = 0.5 * fs
    low = lowcut / nyq
    high = highcut / nyq
    b, a = butter(order, [low, high], btype='band')
    return b, a

def bandpass_filter(data, lowcut, highcut, fs, order=5):
    b, a = butter_bandpass(lowcut, highcut, fs, order=order)
    y = lfilter(b, a, data)
    return y

# 假设data是已经加载的SEGY数据，sampling_rate是采样率
filtered_data = bandpass_filter(data, low, high, sampling_rate)

### 2.2.3 时间-深度转换与数据校正

在地震数据处理中，往往需要将时间域的波形数据转换为深度域数据，以便于更准确地进行地下结构的解释。这通常涉及到速度模型的建立和深度校正。

深度校正需要使用到速度与时间到深度的转换公式，具体为：

\[ Z = \int_{t_0}^{t} v(t') dt' \]

其中，\( Z \)是深度，\( t \)是时间，\( v(t) \)是速度模型，\( t_0 \)是起始时间。速度模型可以通过实验数据或者先验知识获得。

## 2.3 时间序列特征提取

### 2.3.1 基于统计的方法

统计方法是提取时间序列特征的一种基础手段。它们通常用于描述时间序列的中心趋势、分散程度、形状等统计属性。

- 均值（Mean）：时间序列数据的平均值。
- 中位数（Median）：时间序列数据的中位数值。
- 方差（Variance）：时间序列数据的离散程度。
- 标准差（Standard Deviation）：方差的平方根，用于度量数据的波动大小。

通过计算这些统计量，可以了解数据的整体分布情况。

### 2.3.2 频域分析技术

频域分析技术，如傅里叶变换，将时间序列数据从时间域转换到频域，从而分析时间序列的频率成分。

傅里叶变换通过将时间序列分解为不同频率的正弦波和余弦波的和来工作。其基本形式是连续傅里叶变换（CFT），而离散傅里叶变换（DFT）和快速傅里叶变换（FFT）是其在实际应用中的两种更高效形式。

以Python中的`numpy`库为例，以下是一个应用FFT进行频域分析的代码示例：

import numpy as np

# 假设data是已经加载的SEGY数据
n = len(data)
yf = np.fft.fft(data)
xf = np.fft.fftfreq(n)

# 绘制频谱图
import matplotlib.pyplot as plt

plt.plot(xf, np.abs(yf))
plt.show()

执行上述代码后，可以得到数据的频谱图。

### 2.3.3 时频分析方法

时频分析方法是时间序列分析中的一个高级领域，它旨在同时研究信号的时间和频率特性。这些方法能提供信号在特定时间窗口内的频率成分信息，对于非平稳时间序列分析尤为重要。

小波变换是一种常用的时频分析技术，它通过对一系列具有不同时间窗口和中心频率的小波函数进行卷积来分析信号。小波变换能够提供时间分辨率随频率变化的特性。

以Python中的`PyWavelets`库为例，以下是一个应用小波变换进行时频分析的代码示例：

import pywt
import numpy as np
import matplotlib.pyplot as plt

# 假设data是已经加载的SEGY数据
# 选择合适的小波函数和分解层数
wavelet = 'db4'
level = 3

# 小波分解
coeffs = pywt.wavedec(data, wavelet, level=level)

# 重构信号的不同分量
cA, cD = coeffs[0], coeffs[1:]

# 绘制时频图
t = np.linspace(0, len(data), len(data))
plt.figure(figsize=(12, 6))
plt.subplot(level+1, 1, 1)
plt.plot(t, data)
plt.title('Original Signal')
plt.subplot(level+1, 1, 2)
plt.plot(t, cA)
plt.title('Approximation Coefficients')
for i in range(level):
    plt.subplot(level+1, 1, i+3)
    plt.plot(t, cD[i])
    plt.title('Detail Coefficients ' + str(i+1))

plt.tight_layout()
plt.show()

上述代码可以将SEGY数据中的时间序列分解为不同频率的成分，并可视化这些成分随时间的变化情况。

# 3. SeiSee软件在时间序列分析中的应用

## 3.1 SeiSee软件界面和功能概览
SeiSee 是一款专业的地震数据处理软件，它提供了从数据导入、预处理、可视化到高级分析的一系列功能。本部分将介绍如何安装和配置 SeiSee 以及其用户界面的详细功能。

### 3.1.1