【递归到迭代的转换】：JS树遍历算法的革命性改进

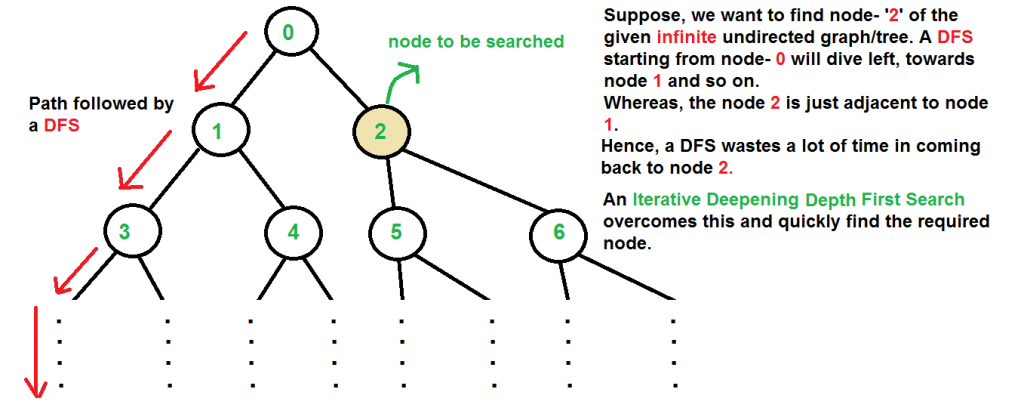
# 1. 树遍历算法概述

在计算机科学中，树是一种重要的数据结构，它以分层的方式存储数据，类似于自然界中的树木。树遍历算法是指系统地访问树中每个节点的过程。在本章中，我们将概述树遍历的基本概念和不同类型的遍历方法。

## 树数据结构简介

树是由节点组成的层次结构，每个节点包含数据和指向其子节点的引用。在树数据结构中，一个节点可能有零个或多个子节点，但只有一个父节点（除了根节点，它没有父节点）。树遍历算法可以分为两大类：深度优先搜索（DFS）和广度优先搜索（BFS）。DFS会尽可能深地访问树的分支，而BFS则逐层从上到下访问树的节点。

## 遍历方法分类

树遍历主要有三种方法：

- 前序遍历（Pre-order Traversal）：访问顺序为根节点 -> 左子树 -> 右子树。
- 中序遍历（In-order Traversal）：访问顺序为左子树 -> 根节点 -> 右子树，对二叉搜索树来说，这种遍历会输出有序的序列。
- 后序遍历（Post-order Traversal）：访问顺序为左子树 -> 右子树 -> 根节点。

这些遍历方法在处理树形结构数据时非常有用，无论是用于搜索、排序还是其他复杂的数据处理任务。在接下来的章节中，我们将深入探讨这些方法，并了解如何在实际应用中进行优化。

树遍历是算法面试中的常见问题，掌握其原理和优化方法对于任何IT专业人员来说都是一项宝贵技能。

# 2. 递归算法基础与复杂性分析

## 2.1 递归算法的基本概念

### 2.1.1 递归函数的工作原理
递归函数通过函数自身调用自身的方式来解决问题。一个递归函数必须至少有一个基本情况（base case）来停止递归，否则会无限循环下去。工作原理可以概括为以下几个步骤：

1. **确定递归终止条件**：这是递归调用的出口，防止无限制的递归调用。
2. **定义问题规模的缩小**：每次递归调用都将问题的规模缩小，以接近终止条件。
3. **执行递归调用**：当前函数实例在问题规模缩小后调用自身，直到达到终止条件。

递归在处理树形数据结构时尤为有用，比如二叉树的深度优先遍历。下面是一个二叉树节点的示例代码，展示了递归函数的基本框架：

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

def print_tree(node):
    if node:
        print(node.val)  # 打印当前节点值
        print_tree(node.left)  # 递归处理左子树
        print_tree(node.right)  # 递归处理右子树

# 示例用法
root = TreeNode(1, TreeNode(2), TreeNode(3))
print_tree(root)

### 2.1.2 递归算法的优点和使用场景

递归算法的优点在于其逻辑清晰，代码简洁，易于理解和维护。当问题可以自然分解为较小的相似问题时，递归算法尤其适用。常见的适用场景包括：

- **树结构遍历**：如二叉树的前序、中序、后序遍历。
- **分治算法**：如快速排序、归并排序、汉诺塔问题。
- **回溯算法**：如解N皇后问题，迷宫问题。
- **动态规划**：有些动态规划问题的状态转移方程天然适合递归求解。

递归算法适合处理具有自然层级关系或者可以通过自相似的问题分解来解决的复杂问题。

## 2.2 递归算法的时间复杂度和空间复杂度

### 2.2.1 时间复杂度的评估
递归算法的时间复杂度通常依赖于递归的深度和每层递归中处理的复杂度。在理想情况下，如果递归深度为`d`，每次递归调用处理的时间为`O(1)`，则总的时间复杂度为`O(d)`。

然而，在树遍历的情况下，如果树是完全不平衡的，递归深度可能会达到`n`（树的高度），造成时间复杂度上升到`O(n)`。

### 2.2.2 空间复杂度的评估和递归栈

空间复杂度是指算法在执行过程中临时占用存储空间的大小。对于递归算法，其空间复杂度主要受到递归栈大小的影响。每次递归调用都会在栈上分配新的帧，因此递归栈的大小等于递归的最大深度。

例如，在一个平衡二叉树中，递归遍历的深度为`O(log n)`，空间复杂度为`O(log n)`。但对于一个完全不平衡的二叉树，空间复杂度可能上升到`O(n)`。

## 2.3 递归算法的性能问题

### 2.3.1 递归调用的开销分析
递归调用的开销主要在于函数调用的栈帧创建、参数传递、返回值处理等。这些操作在每次递归调用时都会发生，随着递归深度的增加，开销也会累积。

### 2.3.2 递归深度限制和解决方案
大多数编程语言对递归深度有限制，以防止栈溢出错误。例如，Python中默认的递归深度限制为1000。如果需要处理更深的递归，可以通过以下方法解决：

- **尾递归优化**：如果编译器或解释器支持尾递归优化，可以将递归改写为尾递归形式以减少栈空间的使用。
- **增加栈空间**：在某些编程环境中，可以手动增加递归深度限制。
- **非递归实现**：将递归算法转换为迭代算法，使用栈或队列模拟递归过程。

## 小结

递归算法以其简洁性和逻辑清晰性在处理具有自然层级关系的问题时尤为强大。然而，递归也带来了空间复杂度增加和栈溢出的风险。在实际应用中，我们必须权衡递归算法的优缺点，并在必要时采用适当的优化措施以提高性能。在接下来的章节中，我们将探讨如何将递归算法转换为迭代算法，以及如何优化递归算法的性能。

# 3. 迭代算法与递归到迭代的转换策略

## 3.1 迭代算法简介

### 3.1.1 迭代与递归的对比

迭代和递归是算法设计中实现重复计算过程的两种基本方法。递归是一种自顶向下的策略，通过函数调用自身来重复解决问题。迭代则是使用循环结构来重复执行一系列操作直到满足特定条件。这两种方法在逻辑上可以互相转换，但各有优缺点。

递归方法通常代码更加简洁，逻辑清晰，易于理解，但可能会增加函数调用栈的开销，特别是在深度递归情况下可能导致栈溢出。迭代方法通常需要维护额外的数据结构，如栈或队列，但往往在空间复杂度和执行速度上有优势。

### 3.1.2 迭代算法的设计思想

迭代算法的设计思想是利用循环结构来逼近问题的解。它通常需要初始化一组状态变量，然后在每次循环迭代中更新这些状态变量，直到达到终止条件。迭代算法强调状态的逐步变化，每一次循环迭代相当于在状态空间中前进一步。

在设计迭代算法时，重要的是确定合适的状态变量、迭代条件和迭代步骤。好的迭代算法能够在每次迭代中都显著地朝着问题的解前进，而不会在无效的状态空间中浪费计算资源。

## 3.2 递归到迭代的转换方法

### 3.2.1 使用栈结构模拟递归过程

递归算法可以转换为迭代算法，其核心思想是使用显式的数据结构（如栈）来模拟隐式的函数调用栈。在递归过程中，函数调用会创建新的执行上下文，而这个上下文通常存储在栈中。通过手动模拟这种栈的行为，我们可以将递归过程转换为迭代过程。

以树的深度优先搜索（DFS）为例，递归实现中会递归地访问每一个节点的子节点。在迭代版本中，我们可以使用一个栈来存