量子计算与OBDD：探索新计算范式的交点


# 摘要
随着量子计算的崛起，有序二进制决策图（OBDD）的概念和应用逐渐受到关注。本文介绍了量子计算的基础理论，包括量子比特、量子门以及OBDD的定义和特性。文章深入探讨了OBDD在量子算法设计和量子计算中的应用，以及量子计算与经典计算的对比分析。此外，本文还讨论了量子计算的前沿技术，包括量子纠缠、量子通信和量子计算的硬件实现，并针对量子计算的安全性问题提出讨论。最后，本文对量子计算的未来展望与OBDD的研究方向进行了预测，重点分析了量子计算的商业化、教育推广和跨学科合作的必要性。

# 关键字
量子计算；OBDD；量子算法；量子纠缠；量子通信；量子硬件实现

参考资源链接：[OBDD：有序二叉决策图的规范表示与应用详解](https://wenku.csdn.net/doc/593v2eaaqc?spm=1055.2635.3001.10343)
# 1. 量子计算的崛起与OBDD概念

量子计算作为计算机科学的一个分支，近年来得到了迅速的发展，并对传统计算范式构成了挑战。其独特之处在于利用量子力学的原理，如叠加态和量子纠缠，实现信息的编码和处理。与经典计算相比，量子计算在特定问题上展现出潜在的巨大优势。

有序二进制决策图（OBDD）是一个在经典计算领域中用于逻辑函数表示和优化的工具，其在数据结构和算法设计中具有重要地位。随着量子计算的崛起，OBDD被引入到量子算法的设计中，以应对量子状态的高复杂性和动态变化特性。

本章将介绍量子计算的兴起背景，探讨OBDD的定义、特性和应用，为理解量子计算和OBDD的后续深入讨论打下基础。接下来，我们将详细探讨量子计算的基本理论和OBDD在其中发挥的作用。

# 2. 量子计算基础理论

### 2.1 量子计算的基本原理

量子计算是建立在量子力学基础之上的全新计算范式，其基本原理与传统经典计算有着根本的不同。量子计算的核心在于量子比特（qubit）和量子门（quantum gate）的应用，这使得量子计算在处理特定问题时展现出超越经典计算的巨大潜力。

#### 2.1.1 量子比特与叠加态

在经典计算中，比特是最基本的信息单位，它只能处于0或1的状态。相比之下，量子比特可以同时处于0和1的状态，这一现象称为量子叠加态。通过叠加态，量子计算机可以同时处理多种可能的组合，为并行计算提供了物理基础。

量子比特的叠加状态可以用以下公式表示：

\[|\psi\rangle = \alpha|0\rangle + \beta|1\rangle\]

其中，\(|\psi\rangle\) 是量子比特的状态，\(\alpha\) 和 \(\beta\) 是复数概率幅，它们的模方分别代表测量得到0或1的概率。重要的是，量子比特的叠加态使得量子计算机在执行某些算法时能够比传统计算机更加高效。

graph LR
A[开始] --> B[初始化量子比特]
B --> C[应用量子门]
C --> D[量子叠加]
D --> E[执行量子算法]
E --> F[测量]
F --> G[结束]

以上流程图展示了量子计算中量子比特从初始化到结束测量的基本步骤。其中，量子门的使用是为了操控量子比特的状态，使系统进入叠加态，从而为量子算法的执行提供基础。

#### 2.1.2 量子门与量子算法

量子门是量子计算中的基本运算单元，它们可以操纵一个或多个量子比特的状态。量子算法就是由一系列量子门的操作构成，其中著名的量子算法包括Shor算法和Grover算法。量子算法通常在叠加态的基础上运行，使得量子计算机在执行算法时能够进行有效的并行处理。

量子门的数学表达一般形式为幺正矩阵（unitary matrix），这保证了量子计算的可逆性。例如，单量子比特的哈达玛门（Hadamard gate）可以表示为：

\[ H = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}\]

应用这个门到一个处于 \(|0\rangle\) 状态的量子比特上，可以得到叠加态：

\[ H|0\rangle = \frac{1}{\sqrt{2}} \left( |0\rangle + |1\rangle \right)\]

量子算法的设计和分析是量子计算领域内最具挑战性的研究方向之一。量子算法不仅需要传统算法的设计技巧，还需要深刻理解量子力学的原理以及量子计算的特点。

### 2.2 有序二进制决策图（OBDD）概述

有序二进制决策图（Ordered Binary Decision Diagrams，OBDD）是一种用于表示和操作布尔函数的数据结构，在经典计算中有着广泛的应用。

#### 2.2.1 OBDD的定义与特性

OBDD是一种用于表示布尔函数的图形化数据结构，它基于二叉决策树，并添加了顺序约束，使得在函数简化和算法优化方面具有优势。OBDD结构由节点和有向边组成，其中节点表示决策变量，边表示变量的取值（0或1），从而构成了一种高度紧凑的表示形式。

OBDD的特性包括：

- **共享子图**：在表示多个具有相似结构的函数时，相同的子图会被共享，节约空间。
- **顺序性**：OBDD中每个决策节点的变量顺序是固定的，这有助于算法的一致性和效率。
- **唯一性**：对于给定的函数和变量顺序，OBDD是唯一的，这简化了分析过程。

graph TD
A[|1\rangle] -->|x1=0| B[|0\rangle]
A -->|x1=1| C[|1\rangle]
B --> D[|0\rangle]
C --> E[|1\rangle]
D --> F[|0\rangle]
E --> F

上图是一个简单的OBDD示例，表示函数 \(f(x_1) = x_1\)。

#### 2.2.2 OBDD在经典计算中的应用

OBDD在经典计算中主要用于布尔函数的优化、逻辑电路的分析与简化、以及电子设计自动化（EDA）领域。例如，在数字电路设计中，OBDD可以有效地进行电路的故障检测和优化。

在软件工程中，OBDD被应用于软件模型检查、程序验证以及测试生成。它能够帮助开发者分析复杂的逻辑条件，从而提升软件的质量和可靠性。

### 2.3 量子计算与经典计算的对比

量子计算与经典计算在模型、原理和算法上存在本质的区别。这些区别既是挑战，也是量子计算潜力的来源。

#### 2.3.1 计算模型的差异分析

经典计算模型以冯·诺依曼架构为基础，侧重于二进制逻辑操作，而量子计算模型则基于量子力学的原理。在经典计算机中，信息是按位进行处理的，而在量子计算机中，信息以量子比特的形式进行表示和操作。这意味着量子计算机可以同时考虑多个可能性，而经典计算机一次只能处理一个。

#### 2.3.2 量子优势与经典算法的局限

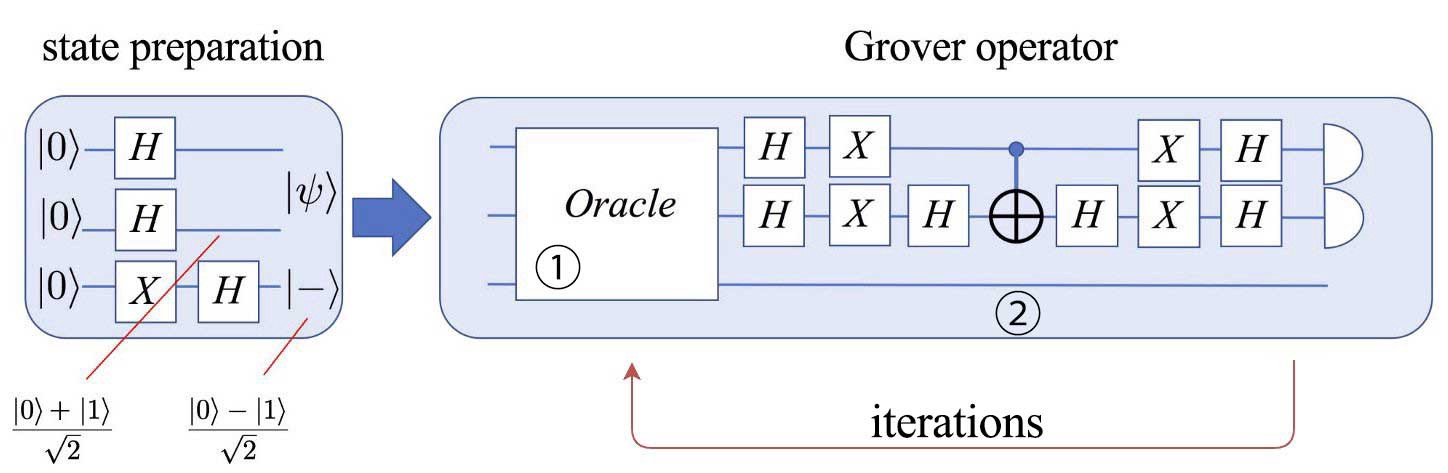
量子优势指的是量子计算机在解决某些特定问题时相比经典计算机所具有的计算优势。尽管当前量子计算机还处于发展阶段，但已有一些算法（如Shor算法和Grover算法）展示了量子计算机相对于经典计算机在特定任务上的明显优势。

经典算法由于其基于经典物理原理的固有限制，在解决如大数质因数分解和搜索无序数据库等特定问题上，其效率远低于量子算法。量子算法的出现，挑战了经典计算理论的某些基本假设，为未来的计算范式提供了新的可能性。

以上内容为第二章的详细章节内容。在下一章节中，我们将继续深入探讨OBDD在量子计算中的应用，及其对量子算法设计的影响。

# 3. OBDD在量子计算中的应用

## 3.1 OBDD在量子算法设计中的作用

### 3.1.1 量子算法中OBDD的构造方法

在量子计算中，有序二进制决策图（OBDD）被提出作为一种图论工具，用于量子算法的设计与优化。量子算法的构造方法通常涉及将量子态和操作编码为OBDD结构，这样做可以简化量子态之间的复杂关系和量子门操作的逻辑结构。

为了构造OBDD，我们首先需要确定量子算法的输入和输出。量子比特的叠加态可以被转化为经典布尔变量，这些布尔变量将构成OBDD的叶子节点。量子门的逻辑操作可以通过布尔逻辑操作来模拟，然后映射为OBDD中的边和内部节点。

以下是一个简单的示例代码，用于构建一个量子算法的OBDD表示：

# 示例代码：构建简单的量子算法OBDD表示

class OBDDNode:
    def __init__(self, var, low=None, high=None, value=None):
        self.var = var  # 变量
        self.low = low  # 0边指向的节点
        self.high = high  # 1边指向的节点
        self.value = value  # 节点的值

def create_obdd_from_quantum_algorithm():
    # 假设我们有一个量子算法，其中的量子比特为q0, q1