深度解析迭代算法的复杂度：揭开算法效率之谜，优化算法性能

# 1. 迭代算法基础**

迭代算法是一种通过重复执行一系列步骤来解决问题的算法。它通过使用循环结构，对数据进行逐个处理，直到达到预期的结果。迭代算法通常用于处理大数据集，因为它可以有效地遍历每个元素。

迭代算法的关键特征是其重复性。它使用循环语句（如 while、for 或 do-while）来控制算法的执行流程。在每次迭代中，算法都会执行一系列操作，并更新数据或状态。这种重复的过程将持续到满足终止条件为止。

# 2. 迭代算法的复杂度分析

### 2.1 时间复杂度

时间复杂度衡量算法执行所需的时间。它表示算法执行所花费的时间与输入规模之间的关系。以下是一些常见的迭代算法的时间复杂度：

#### 2.1.1 常数复杂度

常数复杂度表示算法执行所需的时间与输入规模无关。无论输入规模如何，算法始终执行相同数量的操作。例如：

def find_max(arr):
    max_value = arr[0]
    for i in range(1, len(arr)):
        if arr[i] > max_value:
            max_value = arr[i]
    return max_value

该算法的时间复杂度为 O(n)，其中 n 是数组 arr 的长度。无论数组有多大，算法始终执行 n 次操作（即遍历数组中的每个元素）。

#### 2.1.2 线性复杂度

线性复杂度表示算法执行所需的时间与输入规模成正比。算法执行的操作数量随着输入规模的增加而线性增加。例如：

def sum_array(arr):
    total = 0
    for i in range(len(arr)):
        total += arr[i]
    return total

该算法的时间复杂度为 O(n)，其中 n 是数组 arr 的长度。算法执行 n 次操作（即遍历数组中的每个元素），因此执行时间与输入规模成正比。

#### 2.1.3 对数复杂度

对数复杂度表示算法执行所需的时间与输入规模的对数成正比。算法执行的操作数量随着输入规模的增加而对数增加。例如：

def binary_search(arr, target):
    low = 0
    high = len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1
    return -1

该算法的时间复杂度为 O(log n)，其中 n 是数组 arr 的长度。算法通过将搜索范围对半分来缩小搜索空间，因此执行的操作数量随着输入规模的对数增加。

#### 2.1.4 多项式复杂度

多项式复杂度表示算法执行所需的时间与输入规模的多项式成正比。算法执行的操作数量随着输入规模的增加而多项式增加。例如：

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n - 1) + fibonacci(n - 2)

该算法的时间复杂度为 O(2^n)，其中 n 是输入的数字。算法通过递归调用自身来计算斐波那契数列，因此执行的操作数量随着输入规模的指数增加。

### 2.2 空间复杂度

空间复杂度衡量算法执行所需的空间。它表示算法在执行过程中分配的内存量。以下是一些常见的迭代算法的空间复杂度：

#### 2.2.1 常数空间复杂度

常数空间复杂度表示算法执行所需的空间与输入规模无关。无论输入规模如何，算法始终分配相同数量的内存。例如：

def swap_two_numbers(a, b):
    temp = a
    a = b
    b = temp

该算法的空间复杂度为 O(1)，因为无论输入数字 a 和 b 的值如何，它始终分配 3 个变量（a、b 和 temp）。

#### 2.2.2 线性空间复杂度

线性空间复杂度表示算法执行所需的空间与输入规模成正比。算法分配的内存量随着输入规模的增加而线性增加。例如：

def create_array(n):
    arr = []
    for i in range(n):
        arr.append(i)
    return arr

该算法的空间复杂度为 O(n)，其中 n 是输入的数字。算法分配 n 个元素的数组，因此分配的内存量与输入规模成正比。

#### 2.2.3 多项式空间复杂度

多项式空间复杂度表示算法执行所需的空间与输入规模的多项式成正比。算法分配的内存量随着输入规模的增加而多项式增加。例如：

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n - 1)

该算法的空间复杂度为 O(n)，因为算法通过递归调用自身来计算阶乘，因此分配的内存量随着输入规模的指数增加。

# 3. 迭代算法的优化

### 3.1 时间复杂度优化

时间复杂度优化旨在减少算法执行所需的时间。以下是一些常见的优化技术：

**3.1.1 减少循环次数**

* **使用哨兵变量：**在循环中使用哨兵变量可以提前终止循环，从而减少循环次数。例如：

def find_index(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

* **使用二分查找：**对于已排序的数组，可以使用二分查找算法，该算法的复杂度为 O(log n)，比线性查找的 O(n) 复杂度更优。

**3.1.2 使用更快的算法**

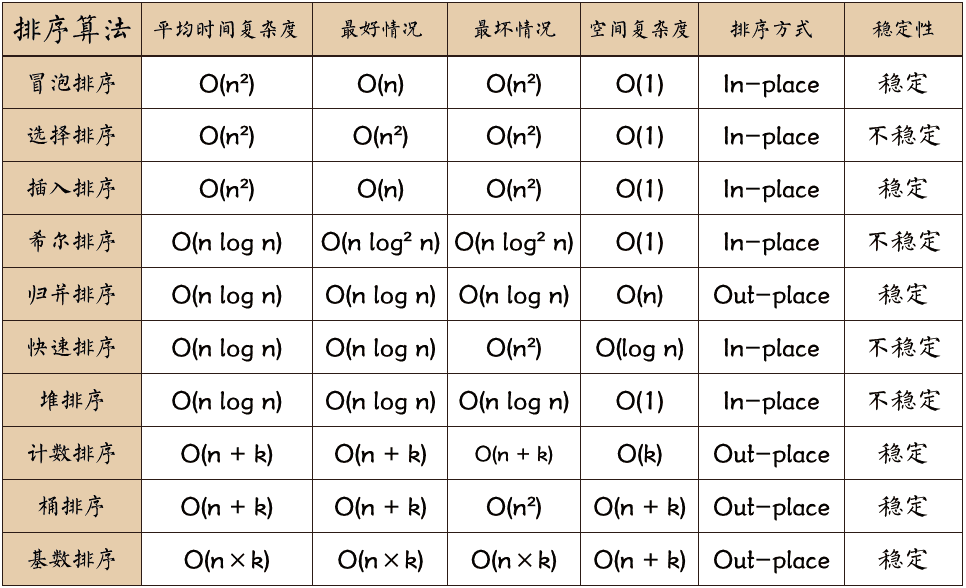
* **选择更优的排序算法：**对于不同的数据规模和类型，不同的排序算法具有不同的复杂度。例如，快速排序在平均情况下具有 O(n log n) 的复杂度，而冒泡排序具有 O(n^2) 的复杂度。
* **使用哈希表：**哈希表可以快速查找和插入元素，其复杂度为 O(1)，比线性搜索的 O(n) 复杂度更优。

**3.1.3 并行化算法**

* **多线程编程：**将算法分解为多个线程并行执行，可以提高执行效率。
* **GPU 加速：**利用 GPU 的并行计算能力，可以大幅提升算法的执行速度。

### 3.2 空间复杂度优化

空间复杂度优化旨在减少算法执行所需的内存空间。以下是一些常见的优化技术：

**3.2.1 减少变量使用**

* **局部变量：**只在函数或代码块中使用的变量，应声明为局部变量，以减少内存占用。
* **复用变量：**避免重复创建变量，而是复用已有的变量，以节省内存空间。

**3.2.2 使用更紧凑的数据结构**

* **位掩码：**使用位掩码可以将多个布尔值存储在一个整数中，从而节省空间。
* **稀疏数组：**对于包含大量空值的数组，可以使用稀疏数组来节省空间，仅存储非空元素。

**3.2.3 延迟加载**

* **惰性求值：**推迟计算或加载数据，直到需要时才执行，从而减少内存占用。
* **按需加载：**仅加载当前需要的部分数据，而不是一次性加载所有数据，以节省内存空间。

# 4. 迭代算法在实际应用中的案例

### 4.1 查找最大值

#### 4.1.1 问题描述

查找给定数组中元素的最大值。

#### 4.1.2 迭代算法

def find_max(arr):
    max_value = arr[0]  # 初始化最大值为数组第一个元素
    for i in range(1, len(arr)):
        if arr[i] > max_value:
            max_value = arr[i]
    return max_value

#### 4.1.3 复杂度分析

**时间复杂度：**O(n)，其中 n 为数组的长度。算法需要遍历数组中的每个元素，因此时间复杂度为线性。

**空间复杂度：**O(1)，算法只使用了一个变量 max_value 来存储最大值，因此空间复杂度为常数。

### 4.2 排序算法

#### 4.2.1 问题描述

将给定数组中的元素按升序或降序排列。

#### 4.2.2 迭代算法：冒泡排序

def bubble_sort(arr):
    for i in range(len(arr) - 1):
        for j in range(len(arr) - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

#### 4.2.3 复杂度分析

**时间复杂度：**O(n^2)，其中 n 为数组的长度。算法需要进行 n-1 次遍历，每次遍历需要比较 n-i 次，因此时间复杂度为平方级。

**空间复杂度：**O(1)，算法不使用额外的空间，因此空间复杂度为常数。

### 4.3 搜索算法

#### 4.3.1 问题描述

在给定数组中查找特定元素。

#### 4.3.2 迭代算法：线性搜索

def linear_search(arr, target):
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

#### 4.3.3 复杂度分析

**时间复杂度：**O(n)，其中 n 为数组的长度。算法需要遍历数组中的每个元素，因此时间复杂度为线性。

**空间复杂度：**O(1)，算法不使用额外的空间，因此空间复杂度为常数。

# 5. 迭代算法的局限性和替代方案

迭代算法虽然在许多情况下非常有用，但它们也有一些局限性。在某些情况下，递归算法、动态规划或贪心算法可能是更好的选择。

### 5.1 递归算法

递归算法是一种通过调用自身来解决问题的算法。递归算法的优点是它们可以非常简洁和优雅。然而，递归算法也可能存在堆栈溢出问题，并且可能难以调试。

**示例：**计算阶乘的递归算法

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

### 5.2 动态规划

动态规划是一种通过将问题分解成较小的子问题并存储子问题的解决方案来解决问题的算法。动态规划的优点是它可以避免重复计算，从而提高效率。然而，动态规划算法可能非常复杂，并且可能难以理解。

**示例：**使用动态规划计算斐波那契数列

def fibonacci(n):
    dp = [0] * (n + 1)
    dp[0] = 0
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

### 5.3 贪心算法

贪心算法是一种通过在每一步做出局部最优选择来解决问题的算法。贪心算法的优点是它们简单且易于实现。然而，贪心算法并不总是能找到全局最优解。

**示例：**使用贪心算法计算活动安排

def activity_selection(activities):
    activities.sort(key=lambda x: x[1])
    selected_activities = [activities[0]]
    last_activity_end_time = activities[0][1]
    for activity in activities[1:]:
        if activity[0] >= last_activity_end_time:
            selected_activities.append(activity)
            last_activity_end_time = activity[1]
    return selected_activities