FFTW3：提升算法速度的关键技巧，让计算飞起来！


# 摘要
本文全面介绍了FFTW3库的各个方面，包括库的概述、快速傅里叶变换（FFT）的原理与应用、FFTW3的安装与配置方法、优化FFT计算性能的策略以及FFTW3在图像与声音信号处理中的实际应用案例。通过对FFTW3库的深入分析，本文强调了高性能计算中FFT的重要性，并探讨了如何通过优化内存访问模式和利用多线程与SIMD指令来提升FFT的计算效率。此外，文章还展示了FFTW3与其他编程语言如Python和MATLAB的集成方式，以及其在分布式和并行计算环境中的应用，旨在为相关领域的开发者提供实用的参考和指导。

# 关键字
FFTW3；快速傅里叶变换（FFT）；信号处理；性能优化；内存访问模式；并行计算

参考资源链接：[FFTW3离散傅里叶变换工具库详细教程与并行计算应用](https://wenku.csdn.net/doc/19jd1itn47?spm=1055.2635.3001.10343)
# 1. FFTW3库概述

FFTW（Fastest Fourier Transform in the West）是一个广泛使用的高性能的离散傅里叶变换（DFT）算法库。FFTW3是FFTW库的第三个主要版本，它支持多维和多线程变换，并在C语言基础上提供了C++接口。这个库的目的是提供一个在各种平台上都能实现最优性能的FFT算法。FFTW3库不仅在学术研究中得到应用，也广泛用于工业界，它支持多种处理器架构，并能够自动选择适应当前硬件的最优计算路径。

在接下来的章节中，我们将深入了解FFT算法的原理、FFTW3库的安装和配置、性能优化方法，以及FFTW3在实际应用中的案例。我们会逐步展开，从基础知识到具体实践，帮助读者全面掌握FFTW3库的使用和优化技巧。

# 2. 理解快速傅里叶变换（FFT）

### FFT的基本原理

#### 离散傅里叶变换（DFT）简介

离散傅里叶变换（DFT）是数字信号处理中的一种基础算法，它将时间域上的离散信号转换为频率域上的离散信号。对于一个长度为N的复数序列\(x_n\)，其DFT定义为复数序列\(X_k\)：

\[ X_k = \sum_{n=0}^{N-1} x_n \cdot e^{-i2\pi kn/N} \]

其中，\(i\)是虚数单位，\(k\)是频率索引（\(0 \leq k < N\)），\(n\)是时间索引。DFT的核心是复指数函数\(e^{-i2\pi kn/N}\)，它作为一个基函数，将时间域的信号分解到不同的频率成分上。

DFT的计算复杂度为\(O(N^2)\)，在处理大规模数据时效率较低。为解决这一问题，库尔特·库利（Cooley）和约翰·图基（Tukey）在1965年提出了一种快速算法，即快速傅里叶变换（FFT），将DFT的计算复杂度降低到\(O(N \log N)\)。

#### FFT算法的数学基础

快速傅里叶变换算法基于分治策略和对称性原理。FFT的主要思想是将原始信号分成更小的子集，并对每个子集递归地应用DFT。通过这种方式，许多计算可以复用，从而极大地减少了计算量。

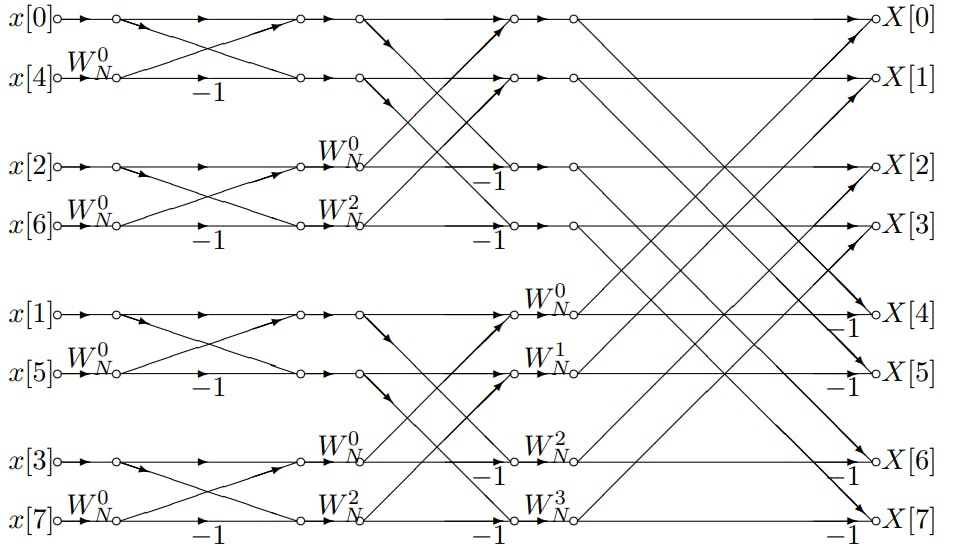
典型FFT算法包括两种基本类型：基于时间抽选（decimation-in-time，DIT）和基于频率抽选（decimation-in-frequency，DIF）。DIT-FFT算法将输入序列按时间抽选分组，而DIF-FFT算法则是按频率抽选分组。在实际应用中，两种算法的具体实现会根据硬件优化进行调整。

### FFT在信号处理中的应用

#### 信号频谱分析

信号的频谱分析是FFT的一个主要应用领域。通过对信号执行FFT，可以得到其在各个频率上的幅度和相位信息，这为信号的频域特性分析提供了重要工具。在频谱分析中，FFT可以用来识别信号的频率成分，检测特定频率的信号，以及滤除不需要的噪声成分。

使用FFT进行频谱分析通常涉及以下步骤：

1. 采集时间域信号。
2. 对信号执行FFT变换。
3. 计算频率分量的幅度和相位。
4. 分析频率分量的分布情况。

#### 信号滤波与调制技术

FFT不仅用于频谱分析，还广泛应用于信号滤波与调制技术。在滤波操作中，FFT可以用于实现快速卷积，其中时域信号的卷积等于其频域表示的逐元素乘积。这可以显著加速数字信号处理中的滤波器设计和应用。

而在调制技术中，FFT用于数字调制解调过程，比如快速傅里叶反变换（IFFT）常被用于生成OFDM（正交频分复用）信号，这是现代无线通信系统中的关键技术之一。

通过FFT，可以将复杂的信号处理算法在频域内进行，从而简化问题，并在许多情况下提高算法效率。FFT的这些应用揭示了其在现代电子系统设计和实现中的中心地位。

# 3. FFTW3的安装和配置

## 3.1 FFTW3库的安装过程

### 3.1.1 环境依赖和安装前准备

FFTW3是一个广泛应用于科学计算中的库，它用于进行快速傅里叶变换（FFT）。安装前，需要确保系统中安装了编译工具，如gcc和make，以及依赖库如glibc和libm。对于不同的操作系统，准备工作也有所不同。

在Linux系统中，大多数发行版都会带有上述依赖包，你可以通过包管理器安装。例如，在Ubuntu系统中，你可以使用以下命令安装所需的依赖：

sudo apt-get update
sudo apt-get install build-essential libopenblas-dev liblapack-dev

在Windows系统中，你可能需要安装Microsoft Visual Studio，并下载预编译的二进制文件或者从源码编译。如果是从源码编译，则需要安装Cygwin或者MinGW来提供必要的类Unix环境。

对于Mac OS系统，通常使用Homebrew作为包管理器。安装FFTW3前，可以使用以下命令安装依赖：

brew install fftw

### 3.1.2 正确安装FFTW3的方法

安装FFTW3的推荐方法是通过下载源码包，然后在本地编译安装。以下是安装的基本步骤：

1. 访问FFTW的官方网站或GitHub仓库下载源码包。
2. 解压源码包到本地目录。
3. 在解压后的源码目录中，通常存在一个名为 `configure` 的脚本，该脚本用于生成特定平台的Makefile文件。
4. 运行 `./configure` 脚本。如果你的系统中没有安装MPI库，不要忘记添加 `--disable-mpi` 参数来禁用MPI支持。
5. 编译源码，运行 `make` 命令。
6. 安装FFTW3，运行 `sudo make install`。

确保在编译过程中没有错误信息，并检查Makefile文件是否正确生成。在 `./configure` 步骤中，如果需要指定安装路径，可以使用 `--prefix=/path/to/your/installation` 参数来指定。

## 3.2 FFTW3库的配置

### 3.2.1 库文件的链接

在开发使用FFTW3的程序时，需要将FFTW3库文件链接到你的应用程序中。链接通常在编译程序时完成。

如果你使用gcc进行编译，链接命令可能如下：

gcc your_program.c -lfftw3 -o your_program

其中 `-lfftw3` 告诉编译器链接FFTW3库。如果你的库安装在非标准路径，可能还需要使用 `-L/path/to/fftw3/lib` 指定库文件的位置。

### 3.2.2 环境变量的设置

在某些情况下，你可能需要设置环境变量以确保系统能够找到FFTW3的库文件和头文件。对于Linux和Mac OS，可以在用户家目录下的 `.bashrc` 或 `.zshrc` 文件中添加以下环境变量：

export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/path/to/fftw3/lib
export CPATH=$CPATH:/path/to/fftw3/include

在Windows系统中，可以通过系统属性设置环境变量，或者在命令行中临时设置：

set PATH=%PATH%;C:\path\to\fftw3\bin
set INCLUDE=C:\path\to\fftw3\include;%INCLUDE%
set LIB=C:\path\to\fftw3\lib;%LIB%

确保将 `/path/to/fftw3/` 替换为实际的安装路径。这样设置后，编译器和链接器就能找到FFTW3库文件，你的应用程序就可以使用FFT算法了。

# 4. 优化FFT计算性能

## 4.1 内存和计算优化策略
### 4.1.1 内存访问模式对性能的影响
在进行FFT计算时，内存访问模式对性能有显著的影响。这是因为内存的读取和写入速度远低于CPU的处理速度，内存访问成为了性能瓶颈之一。为了优化内存访问模式，我们应采取连续存储、减少缓存未命中和内存对齐等策略。

- **连续存储**：尽量使用连续的内存块，以减少CPU缓存未命中的次数。例如，在C语言中使用指针数组时，若数组连续，则可以有效地利用缓存。

// 使用指针数组指向连续内存块的示例
double *data = (double *) fftw_malloc(sizeof(double) * N);
fftw_plan_with_nthreads(FFTW_THREADS);
fftw_plan p = fftw_plan_dft_r2c_1d(N, data, out, FFTW_ESTIMATE);

- **减少缓存未命中**：避免随机访问内存，尽量按顺序读取或写入，减少缓存未命中率。

- **内存对齐**：内存对齐可以提升内存访问速度，特别是在使用SIMD指令集时。例如，利用编译器指令`__attribute__((aligned(N)))`来确保数据结构的内存对齐。

### 4.1.2 多线程和SIMD指令的利用
多线程和单指令多数据(SIMD)指令集是现代处理器提供的两种并行计算资源，它们可以显著提升FFT计算性能。

- **多线程**：利用多核处理器的并行计算能力，可以实现算法的多线程执行。FFTW3库提供了线程支持，可以通过设置环境变量`FFTW_THREADS`或使用`fftw_plan_with_nthreads()`函数来指定线程数。这样，FFT计算可以根据线程数自动分配到不同的核心上执行。

// 设置并行线程数
fftw_plan_with_nthreads(4); // 使用4个线程进行计算

- **SIMD指令集**：现代处理器通常包含如SSE或AVX等SIMD指令集，这些指令集允许单条指令同时处理多个数据元素。FFTW3在编译时可以通过特定的编译标志来启用这些指令集的支持，从而提高FFT计算效率。例如，在gcc编译器中使用`-msse2`或`-mavx`标志。

## 4.2 计算实例与性能分析
### 4.2.1 FFTW3计算实例
本小节提供一个使用FFTW3库进行FFT计算的简单实例，以展示其API的使用方法及性能。

#include <fftw3.h>
#include <stdio.h>
#include <math.h>

int main() {
    int N = 1024; // 定义FFT点数
    fftw_complex *in, *out;
    fftw_plan p;

    // 分配输入输出数组
    in = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);
    out = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * N);

    // 初始化输入数据
    for (int i = 0; i < N; ++i) {
        in[i][0] = cos(5.0 * 2.0 * M_PI * i / N); // 实部
        in[i][1] = 0.0; // 虚部
    }

    // 创建计划并执行FFT
    p = fftw_plan_dft_1d(N, in, out, FFTW_FORWARD, FFTW_ESTIMATE);
    fftw_execute(p);

    // 执行FFT变换
    fftw_destroy_plan(p); // 销毁计划
    fftw_free(in); // 释放内存
    fftw_free(out);

    return 0;
}

### 4.2.2 性能测试与调优技巧
性能测试是优化工作的重要环节。我们可以通过编写简单的测试脚本，使用时间函数（如`clock()`或`gettimeofday()`）来测量FFT执行时间，并结合系统资源监控工具（如`top`或`htop`）来观察CPU的使用情况和内存占用。

调优FFT计算性能的一些技巧包括：

- **选择合适的FFT算法和计划**：FFTW3库允许根据不同的场景选择合适的FFT算法。例如，在不关心计算精度的场合，可以使用`FFTW_ESTIMATE`来获取更快的计划。
- **利用预处理数据**：如果需要对相同的数据多次进行FFT变换，可以先计算一次`FFTW_PATIENT`或`FFTW_EXHAUSTIVE`计划，然后保存结果以供后续使用。
- **减少数据复制**：在多线程环境中，避免不必要的数据复制可以提高性能。使用FFTW3的计划执行函数，可以直接在原数组上工作。

通过上述策略，我们可以得到更优的FFT计算性能。然而，具体调优还需视应用的复杂性和硬件环境而定，建议进行详尽的测试以找到最佳配置。

# 5. FFTW3的实际应用案例

## 5.1 图像处理中的FFT应用

### 5.1.1 图像增强与恢复

快速傅里叶变换（FFT）在图像处理领域中有广泛的应用，特别是在图像增强与恢复方面。图像增强通常涉及提高图像的对比度、清晰度或突出其特定的特征。FFT提供了一种将图像从空间域转换到频域的方法，使得针对图像频谱的处理成为可能。

在频域中，高频通常对应于图像的边缘和细节，而低频对应于图像的平滑部分。通过在频域中应用不同的滤波器，可以对图像进行增强或恢复。例如，使用低通滤波器可以减少噪声，而高通滤波器则有助于锐化图像边缘。

#### 图像增强的FFT步骤：

1. **读取图像并转换为灰度（如果需要）**
2. **应用FFT**
3. **设计滤波器（如低通、高通、带通或带阻）**
4. **将滤波器应用于频谱**
5. **执行逆FFT来获得处理后的图像**

下面是一个使用Python和FFTW3库进行图像增强的代码示例：

import numpy as np
import imageio
from fftw3 import fft, ifft

# 读取图像并转换为灰度
image = imageio.imread('image.png', pilmode='L')
image = np.array(image, dtype=np.float32)

# 执行FFT
image_fft = fft(image)

# 设计低通滤波器
n, m = image.shape
crow, ccol = n // 2, m // 2
mask = np.zeros((n, m), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1
filter = np.fft.fftshift(mask)

# 应用滤波器
image_fft_filtered = image_fft * filter

# 执行逆FFT
image_ifft = ifft(image_fft_filtered)
image_ifft = np.abs(image_ifft)

# 保存处理后的图像
imageio.imwrite('image_enhanced.png', image_ifft.astype(np.uint8))

在上述代码中，我们首先将图像转换为灰度值的浮点数数组。然后，我们对图像执行FFT，并设计一个简单的低通滤波器，其目的是保留图像中心的低频分量。滤波器通过乘法应用到频谱上，最后进行逆FFT得到处理后的图像。通过这种方式，我们能够增强图像的整体效果，例如减少噪声，或者强化边缘信息。

### 5.1.2 图像压缩技术

图像压缩的目标是在尽可能减少信息损失的情况下，减少图像文件的存储空间或传输带宽的需求。FFT是许多图像压缩技术的核心组件，特别是在有损压缩算法中。

通过将图像转换到频域，FFT允许我们根据人类视觉系统的特性来去掉一些不太重要的信息。例如，JPEG压缩算法就是利用了人类视觉对高频信息不敏感的特性，对高频分量进行量化和舍弃，从而达到压缩的目的。

#### 基于FFT的图像压缩步骤：

1. **将图像转换为频域**
2. **对频谱分量进行量化**
3. **舍弃量化后值较小的分量**
4. **对剩余分量执行逆FFT得到压缩后的图像**

使用FFT进行图像压缩的代码可能与上面的图像增强代码类似，但是在这一步骤中，我们设计的滤波器可能会更加精细，并且量化过程需要根据压缩标准来确定。

## 5.2 声音信号处理

### 5.2.1 音频频谱分析

在声音信号处理中，FFT同样是一个强大的工具。声音信号的频谱分析可以用于音乐制作、语音分析和诊断声音问题。通过将声音信号转换到频域，FFT帮助我们理解声音信号的组成频率成分。

在音乐制作中，音频频谱分析可以用来调整音乐作品的音质，提高特定频率成分，或者减少不需要的噪音。对于语音分析，频谱可以用来识别说话者的语音特征，甚至用来实现声纹识别。

#### 频谱分析的FFT步骤：

1. **录音或读取声音文件**
2. **应用FFT到声音信号**
3. **分析频谱以识别特征频率**
4. **根据分析结果进行声音处理**

### 5.2.2 声音去噪与回声消除

声音去噪和回声消除是FFT在声音信号处理中应用的另一个重要领域。通过频谱分析，我们可以识别出哪些频率成分是非预期的噪声，并相应地进行过滤。

例如，在电话通话中，回声消除技术利用FFT来分离近端讲话者的声音和远端讲话者的声音，从而消除回声。通过识别和抑制延迟和回声的频率分量，可以提高语音通讯的清晰度。

#### 声音去噪和回声消除的FFT步骤：

1. **收集声音信号**
2. **应用FFT来分析信号的频谱**
3. **设计滤波器以分离信号和噪声**
4. **应用滤波器并执行逆FFT以获得去噪的声音**
5. **对于回声消除，进一步处理以抑制远端信号的复制**

去噪和回声消除是FFT应用在声音信号处理中的两个具体例子，实际的实现可能会根据具体的应用场景有所不同。通过仔细设计滤波器和分析声音信号的频谱特征，我们可以有效地提升声音信号的质量和可理解性。

# 6. FFTW3与其他库的集成

在现代的软件开发中，跨语言的库集成已经成为了一个重要的趋势。FFTW3作为一个强大的FFT算法库，其集成到其他编程语言及高性能计算环境中的能力，极大地扩展了它的应用范围。本章将详细介绍如何将FFTW3集成到Python和MATLAB中，并讨论其在分布式计算和并行计算环境下的应用。

## 6.1 集成到其他编程语言

### 6.1.1 FFTW3与Python的集成

Python因其简洁的语法和强大的社区支持，在数据科学和工程领域得到了广泛应用。将FFTW3集成到Python中，可以帮助Python用户利用FFTW3强大的FFT算法库来处理复杂的数据分析问题。

为了在Python中使用FFTW3库，我们可以借助`ctypes`模块或者更高级的封装，如`numpy`的`fft`模块。以下是使用`ctypes`模块进行集成的步骤：

1. 下载并安装FFTW3库。
2. 在Python脚本中，使用`ctypes`导入FFTW3库。
3. 将Python数据类型转换为FFTW3支持的类型，并进行FFT计算。
4. 将计算结果转换回Python的数据类型，并进行后续处理。

import ctypes
import numpy as np

# 加载FFTW3库
fftw_lib = ctypes.CDLL('libfftw3-3.so')

# 初始化输入输出数组
n = 8
data_in = np.array(range(n), dtype=np.complex128)
data_out = np.zeros(n, dtype=np.complex128)

# 转换Python数据为FFTW3可用的数据类型
fftw_lib.fftw_plan_with_nthreads.restype = ctypes.c_void_p
fftw_plan = fftw_lib.fftw_plan_dft_1d(n, data_in.ctypes.data_as(ctypes.POINTER(ctypes.c_double complex)),
                                      data_out.ctypes.data_as(ctypes.POINTER(ctypes.c_double complex)),
                                      fftw_lib.FFTW_FORWARD, fftw_lib.FFTW_ESTIMATE)

# 执行FFT计算
fftw_lib.fftw_execute(fftw_plan)

# 清理FFTW3计划
fftw_lib.fftw_destroy_plan(fftw_plan)

# 查看结果
print(data_out)

通过上述步骤，可以完成FFTW3与Python的简单集成，并进行FFT计算。

### 6.1.2 FFTW3与MATLAB的集成

MATLAB是另一个广泛使用的数值计算和可视化平台，它的内置FFT函数由于其便捷性而受到青睐。然而，对于需要高性能FFT计算的用户来说，集成FFTW3到MATLAB提供了更多的可能性。

在MATLAB中集成FFTW3库相对简单，MATLAB允许直接调用动态链接库（DLL）中的函数。以下是在MATLAB中集成FFTW3的步骤：

1. 下载并安装FFTW3库。
2. 设置MATLAB的动态链接库路径，确保MATLAB能正确调用FFTW3的函数。
3. 使用MATLAB的`calllib`函数调用FFTW3的相关函数。

% 设置FFTW3库路径
setenv('LD_LIBRARY_PATH', ['/path/to/fftw/lib' getenv('LD_LIBRARY_PATH')]);

% 加载FFTW3库
fftw = calllib('libfftw3-3', 'fftw3');

% 初始化输入输出数组
n = 8;
data_in = (0:n-1) + 1i * (0:n-1);
data_out = zeros(n, 1);

% 执行FFT计算
fftw('fftw_plan_dft_1d', n, data_in, data_out, 1, 'FFTW_ESTIMATE');

% 显示结果
disp(data_out);

以上代码展示了如何在MATLAB中使用FFTW3执行FFT计算。通过这种方式，MATLAB用户可以利用FFTW3的高性能特性来处理复杂的数据集。

## 6.2 高性能计算（HPC）中的应用

### 6.2.1 分布式FFT计算

在高性能计算环境中，数据集可能过于庞大以至于无法在单一机器上处理。分布式FFT计算允许将数据分割到多台计算机上，分别处理后再合并结果，从而实现对大规模数据集的处理。

分布式FFT计算的步骤包括：

1. 将输入数据分割并分配到多个计算节点。
2. 在每个节点上执行局部FFT计算。
3. 使用全局FFT算法合并局部计算结果。

分布式FFT计算通常需要定制的算法和通信协议来优化数据传输和计算负载均衡。

### 6.2.2 并行计算环境下的FFTW3应用

并行计算环境（如使用MPI的集群）为FFT计算提供了强大的计算能力。FFTW3库本身就支持多线程和SIMD指令集，这为在并行计算环境下提升FFT计算性能提供了基础。

在并行计算环境中应用FFTW3，主要步骤包括：

1. 初始化并行环境，如通过MPI初始化。
2. 根据计算节点的数目，合理分配数据和计算任务。
3. 在每个计算节点上，执行FFTW3的多线程FFT计算。
4. 同步各个节点的结果，并进行必要的数据合并。

利用并行计算环境和FFTW3的并行能力，可以显著提升大规模FFT计算的速度，从而在科学计算、数据分析等领域发挥重要作用。

在本章节中，我们介绍了FFTW3在不同编程语言中的集成方法以及在高性能计算环境中的应用。通过这些内容，读者可以了解到如何将FFTW3更有效地融入现有的计算框架，实现复杂计算任务的高效处理。