布尔代数与逻辑门的交响:离散数学与电子学融合的5大原理
发布时间: 2025-01-10 20:52:02 阅读量: 5 订阅数: 4 


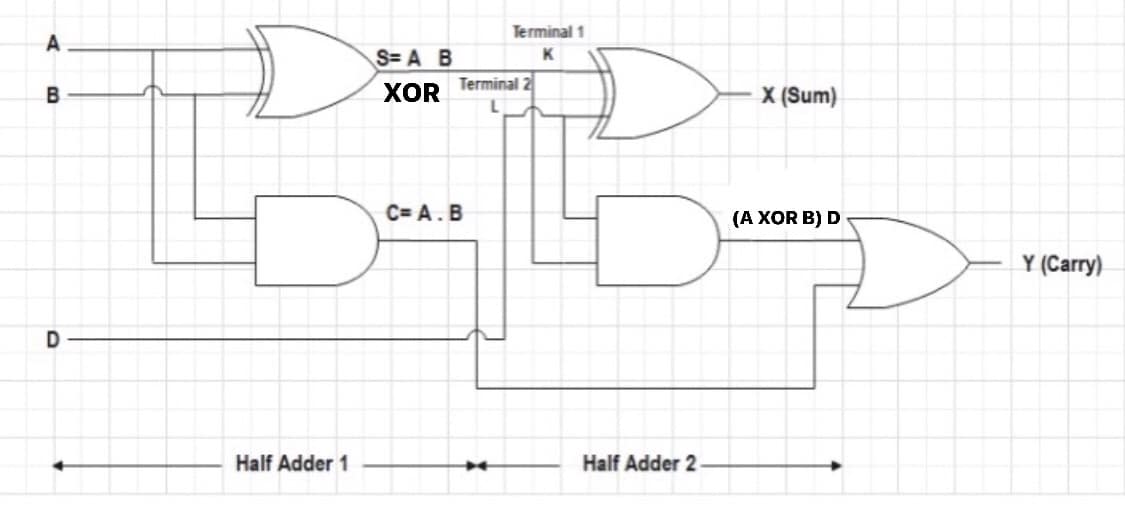
数字逻辑与工程设计PDF课件 chp2-2布尔代数基础.pdf
# 摘要
本文旨在探究布尔代数的起源与基础,分析逻辑门在电子学中的实现和应用,并讨论布尔代数在数字电路设计中的关键作用。文章首先介绍布尔代数的历史背景和基本原理,然后深入讲解逻辑门的概念、类型以及在电路中的应用。第三章着重于布尔代数在简化和优化电路设计中的应用,展示从布尔表达式到电路图的转换方法。文章接着讨论了逻辑门在电子学中的构建原理,包括物理层面的细节和动态特性。最后,通过理论与实践相结合的案例分析,本文探讨了布尔代数与逻辑门如何在解决复杂问题和实际电路设计中发挥作用,以及它们在教学和研究中的创新应用。
# 关键字
布尔代数;逻辑门;数字电路设计;电子学原理;理论与实践;集成电路优化
参考资源链接:[离散数学(第五版)习题和答案](https://wenku.csdn.net/doc/6412b690be7fbd1778d472dc?spm=1055.2635.3001.10343)
# 1. 布尔代数的起源与基础
布尔代数是现代计算机科学的数学基础之一,它由乔治·布尔在19世纪中叶首次提出。布尔代数的核心思想是利用代数的方法描述和分析逻辑关系。与传统数学不同,布尔代数使用逻辑运算代替传统的算术运算,其中包含的基本运算有“与”、“或”和“非”,分别对应布尔运算中的AND、OR和NOT。
## 1.1 布尔代数的历史背景
### 1.1.1 布尔代数的创立者
乔治·布尔是一位英国数学家,他在1854年出版的著作《思维规律的研究》中奠定了布尔代数的基础。布尔代数最初并非为电子计算机设计,而是一种用于逻辑推理和证明的数学工具。
### 1.1.2 数学逻辑的发展与影响
布尔代数的出现,开启了数学逻辑研究的新纪元。其影响深远,不仅推动了计算机科学的发展,也影响了形式逻辑、认知科学及人工智能等多个领域。
## 1.2 布尔代数的基本原理
### 1.2.1 逻辑变量与运算符
在布尔代数中,变量通常表示逻辑命题,其取值为“真”(True)或“假”(False),布尔运算符则定义了逻辑变量之间的运算规则。这些基础的运算符构成了现代计算机逻辑运算的核心。
### 1.2.2 布尔代数的基本定律和定理
布尔代数中的基本定律和定理,如幂等律、交换律、结合律等,为逻辑运算提供了清晰的规则。这些定律不仅对理论逻辑学有重要意义,也为数字电路的设计提供了直接指导。
## 1.3 布尔函数与真值表
### 1.3.1 真值表的构造和解读
真值表是布尔函数的直观表现形式,通过表格列出所有可能的变量组合及其对应结果,为理解和实现逻辑关系提供了基础工具。
### 1.3.2 布尔函数的简化与标准化
简化的布尔函数不仅能够减少实现的复杂性,还能提高电路的效率。通过运用布尔代数的定律和定理,我们可以将布尔函数化简为更加简洁的形式,进而优化电路设计。
布尔代数的诞生,为后续电子计算机的设计和发展奠定了坚实的理论基础。它的原理被广泛应用于计算机逻辑设计、数字电路分析以及现代电子技术中。随着技术的发展,布尔代数将继续在多个领域中发挥其不可替代的作用。
# 2. 逻辑门的实现与应用
逻辑门是构成数字电路的基本单元,它们代表了布尔代数中逻辑运算的基本实现。在这一章节中,我们将探讨逻辑门的概念、它们的电子实现原理、在电路中的应用以及现代应用实例。
### 2.1 逻辑门的基本概念
#### 2.1.1 逻辑门的类型与符号
逻辑门是将一个或多个二进制输入转换为一个二进制输出的电子设备。它们执行的是布尔代数中定义的逻辑运算,如AND、OR和NOT等。这些基本逻辑门的符号和功能如下表所示:
| 逻辑门类型 | 符号 | 功能描述 | 真值表 |
| --- | --- | --- | --- |
| AND | |
| OR | |
| NOT | |
这些基本逻辑门可以进一步组合形成更复杂的逻辑电路。
#### 2.1.2 逻辑门的电子实现原理
从电子层面来看,逻辑门通常由半导体设备(如晶体管)实现。例如,在CMOS(互补金属氧化物半导体)技术中,逻辑门是由N型和P型MOS晶体管组合而成。基本的NAND和NOR门可以用CMOS技术实现,因为它们是CMOS逻辑的构建模块。
```cmos
// CMOS NAND 门电路示例
// P型晶体管连接在一起,N型晶体管连接在一起
// 逻辑上,P型晶体管在输入为低电平时导通,N型晶体管在输入为高电平时导通
// 伪代码描述
P-Type: 如果 A 和 B 都为1,则 输出为0(导通)
N-Type: 如果 A 和 B 至少有一个为0,则 输出为1(导通)
```
### 2.2 逻辑门在电路中的应用
#### 2.2.1 组合逻辑电路与时序逻辑电路
逻辑门可以用于构建组合逻辑电路和时序逻辑电路。组合逻辑电路的输出仅依赖于当前的输入值,而时序逻辑电路的输出还依赖于过去的输入值,因为它们包含存储元素(如触发器)。
组合逻辑电路的一个常见例子是算术逻辑单元(ALU),它执行算术和逻辑运算。时序逻辑电路的一个例子是触发器,用于存储和记忆电路状态。
#### 2.2.2 逻辑门电路的设计与实现
设计和实现逻辑门电路需要一系列步骤。首先,根据需求分析确定电路的功能。然后,可以使用布尔代数简化逻辑表达式,接着设计电路图,最后进行电路的搭建和测试。
下面是一个简单的逻辑门电路设计流程:
```mermaid
flowchart LR
A[需求分析] --> B[布尔优化]
B --> C[绘制电路图]
C --> D[电路搭建]
D --> E[电路测试]
```
### 2.3 逻辑门的现代应用实例
#### 2.3.1 微处理器与计算机硬件
逻辑门是微处理器的基础,每个晶体管或晶体管对都可以看作一个逻辑门。微处理器内部包含数百万个逻辑门,它们协同工作执行复杂的指令集。
```mermaid
graph LR
A[二进制输入] -->|通过逻辑门| B[ALU]
B --> C[寄存器]
C --> D[存储器]
D --> E[输入/输出]
```
#### 2.3.2 逻辑门在数字通信中的作用
在数字通信领域,逻辑门用于构建调制解调器、编码器和解码器等设备。它们用于执行信号编码、解码、同步等关键功能。
```mermaid
graph LR
A[信息输入] --> B[编码器]
B -->|逻辑门处理| C[调制器]
C --> D[传输介质]
D -->|通过解调| E[解码器]
E --> F[信息输出]
```
通过上述各小节的分析,逻辑门的实现与应用在数字电路设计中发挥着重要的作用,从基本的电子实现到复杂的微处理器和数字通信系统中,逻辑门都是不可或缺的组成部分。在接下来的章节中,我们将进一步深入探讨布尔代数在数字电路设计中的应用以及电子学中逻辑门构建原理的具体内容。
# 3. 布尔代数在数字电路设计中的作用
在数字电路设计领域,布尔代数不仅是基础理论,更是指导实践的重要工具。布尔逻辑提供了一种系统化的方法,用以表示复杂的电子电路关系。本章节将深入探讨布尔代数如何在电路设计中扮演关键角色,展示它如何简化设计流程、优化逻辑电路,并在集成电路设计中得到广泛应用。
## 3.1 布尔代数的电路设计方法
布尔代数之所以在电路设计中至关重要,是因为它能以一套严格的形式化规则来表达和处理逻辑关系。设计人员可利用这些规则简化复杂电路的逻辑表达式,从而减小所需的电路元件数量,并提高电路性能。
### 3.1.1 用布尔代数简化电路设计
简化是数字电路设计中的一个关键步骤,它有助于减少所需的逻辑门数量,降低成本,并提高电路的可靠性。布尔代数提供了一系列代数定律和定理,如德摩根定律、分配律等,这些都是用来简化表达式的基本工具。
```mermaid
graph LR
A[布尔表达式] -->|简化| B[简化后的布尔表达式]
B --> C[逻辑门电路图]
```
例如,考虑一个逻辑表达式 `(A AND B) OR (A AND NOT B)`。通过应用布尔代数的分配律,我们可以将其简化为 `A`。这意味着原本需要一个 OR 门和两个 AND 门的电路,可以只用一个连接到 A 的输入上即可。
### 3.1.2 利用布尔代数进行逻辑优化
逻辑优化的目标是减小电路的物理尺寸,降低功耗,提高速度和可靠性。这通常涉及到重组电路的逻辑结构,以减少逻辑门数量、优化信号路径或减少信号传播延迟。
考虑以下布尔表达式:
```
F = ABC + ABCD + ABCDEF
```
通过布尔代数的吸收定律 `A + AB = A`,可以简化为:
```
F = ABC + CD + EF
```
这个简化可能显著减少了所需的逻辑门数量,从而优化了整个电路。
## 3.2 从布尔表达式到电路图
将布尔表达式转换成可视化的电路图是数字电路设计的核心步骤。理解这一转换过程不仅需要逻辑学知识,还需要对电路图符号与构成元件有透彻的理解。
### 3.2.1 表达式转换为电路图的方法
转换布尔表达式为电路图时,需要使用标准的符号表示逻辑门,例如,AND 门用 ∧ 表示、OR 门用 ∨ 表示,NOT 门用非符号表示。考虑一个布尔函数 F = (A AND B) OR (C AND NOT D),可以按照以下步骤进行转换:
1. 根据逻辑运算符,画出相应的逻辑门。
2. 将输入变量和它们的反向作为门的输入。
3. 将输出连接起来形成最终的电路。
### 3.2.2 优化电路图的设计流程
电路图的优化通常分为两个层面:
1. **逻辑优化**:在电路图设计之前,使用布尔代数规则简化表达式。
2. **物理优化**:根据实际制造和物理限制,调整门的位置和连接以减小延迟和功耗。
```mermaid
graph LR
A[布尔表达式简化] --> B[初步电路图设计]
B --> C[逻辑优化]
C --> D[物理优化]
D --> E[最终电路图]
```
## 3.3 布尔代数在集成电路中的应用
随着集成电路技术的发展,设计者面对的挑战是如何在有限的空间内设计出尽可能高效的电路。布尔代数在这一过程中扮演着至关重要的角色。
### 3.3.1 集成电路的布尔设计挑战
设计集成电路时,需要考虑门的尺寸、布局和信号传递的延时等。在这些挑战中,布尔代数能够通过逻辑优化帮助减小所需的晶体管数量,进而减小芯片面积和降低功耗。
### 3.3.2 高级布尔优化技术在IC设计中的应用
高级布尔优化技术,如门级优化和逻辑重构,可以进一步提高集成电路的性能。门级优化涉及重新排列和合并逻辑门,而逻辑重构是指重新构造布尔表达式以更好地映射到物理硬件上。
布尔代数为数字电路设计者提供了强有力的理论基础和实用工具,从简化设计到优化电路,它在各个层面都发挥着核心作用。通过布尔代数,设计者能够构建出更高效、更可靠的数字电路系统,这对于现代电子设备和信息技术的发展至关重要。
# 4. 电子学中的逻辑门构建原理
逻辑门是数字电路中不可或缺的基础构件,它们决定了电路的逻辑功能和性能。在本章节中,我们将深入了解逻辑门的物理构建原理、动态特性和高级功能的实现方式。从微观层面理解逻辑门如何构建,可以帮助我们更好地设计和优化数字电路。
### 4.1 逻辑门的物理层面
#### 4.1.1 二极管、晶体管和逻辑门
在构建逻辑门的过程中,二极管和晶体管是最基础的电子元件。二极管是单向导电的,只允许电流向一个方向流动。而晶体管可以作为开关使用,控制电流的流动。在CMOS技术中,n型和p型晶体管被用来构建逻辑门。CMOS技术的优势在于它具有较低的功耗和较好的电气特性,这使得它成为现代逻辑门构建的首选技术。
#### 4.1.2 CMOS技术与逻辑门的设计
CMOS(互补金属氧化物半导体)技术的核心在于使用一对互补的n型和p型MOSFET(金属氧化物半导体场效应晶体管)。在CMOS逻辑门中,一个晶体管的源极连接到电源,另一个连接到地。通过合理配置这两个晶体管的开关状态,可以实现逻辑门的功能。例如,一个简单的CMOS反相器可以通过一个p型晶体管(上拉晶体管)和一个n型晶体管(下拉晶体管)来构建,它们分别控制输出从高电平到低电平以及从低电平到高电平的转换。
### 4.2 逻辑门的动态特性
#### 4.2.1 延迟、扇出与噪音容限
逻辑门的动态特性是指它在实际电路中运行时的各种参数特性。延迟(Propagation Delay)是指输入信号变化后,输出信号相应变化所需的时间。扇出(Fan-Out)是指一个逻辑门可以驱动多少个相同逻辑门的输入端。噪音容限(Noise Margin)是指逻辑门在不改变输出状态的情况下,输入信号能够承受的最大噪声电压。理解并优化这些特性对于保证数字电路的可靠性和性能至关重要。
#### 4.2.2 动态逻辑与锁存器电路
动态逻辑门通常使用电容器存储逻辑值,并在特定的时钟阶段进行充电和放电。这种方法可以减少晶体管的数量,从而减小芯片面积和功耗。动态逻辑门的关键在于时钟信号的精确控制。锁存器电路(如D型锁存器)是另一种重要类型的动态逻辑,它用于存储数据。在设计锁存器时,要考虑到建立时间(Setup Time)、保持时间(Hold Time)以及可能的锁存器冲突,这些都是确保数据正确传输的关键因素。
### 4.3 逻辑门的高级功能实现
#### 4.3.1 三态逻辑门与缓冲器
三态逻辑门(Tri-State Logic Gate)除了逻辑高(1)和逻辑低(0)之外,还有一种高阻态(Hi-Z),它使得输出不驱动任何电流。这在总线系统中非常有用,因为同一总线上可以连接多个三态逻辑门,通过控制各自的使能信号,可以实现对总线的控制和数据传输。缓冲器(Buffer)是一种特别的三态逻辑门,它能够增强信号的驱动能力,经常用于驱动长线负载或者作为电平转换器。
#### 4.3.2 可编程逻辑设备与FPGA
可编程逻辑设备允许在不改变硬件的情况下重新配置逻辑门的连接方式和功能。其中,现场可编程门阵列(FPGA)是目前最常用的可编程逻辑设备。FPGA包含了大量的可编程逻辑块和可编程互连,工程师可以通过硬件描述语言(HDL)来定义逻辑块的功能以及它们之间的连接关系。FPGA的灵活性和高性能使得它成为逻辑门高级功能实现的重要平台。
```verilog
// 示例:Verilog代码片段,描述一个简单的D型锁存器
module D_latch(
input wire D, // 数据输入
input wire En, // 使能信号
output reg Q // 输出
);
always @(D or En)
if (En)
Q <= D; // 当使能信号为高时,锁存器输出跟随数据输入
endmodule
```
在上述Verilog代码片段中,描述了一个简单的D型锁存器。这是一个典型的同步逻辑电路,其中`always`块使用了一个敏感列表,它会在输入`D`或使能信号`En`发生改变时触发。当使能信号`En`为高时,D型锁存器会将其输入`D`的状态传递到输出`Q`。这个代码的逻辑分析显示了锁存器如何根据使能信号的变化来控制数据流。
逻辑门的构建原理不仅限于物理层面,它还涉及到逻辑功能的实现与优化。通过理解逻辑门如何响应不同的输入条件和信号特性,我们可以更加高效地设计和实现复杂的数字电路。在电子工程的研究和实践中,逻辑门的构建原理是实现创新和解决实际问题的基础。
# 5. 布尔代数与逻辑门的交响:理论与实践结合的案例分析
在探索了布尔代数的原理和逻辑门的实际应用后,本章节将把理论与实践紧密结合,通过具体案例分析来展示如何运用布尔代数来解决复杂的工程问题,并将理论知识转化为实际电路设计。本章节旨在通过实例加深读者对于布尔代数和逻辑门在现代电子工程中应用的理解。
## 5.1 理论应用:解决复杂问题的布尔代数方法
### 5.1.1 问题定义与布尔建模
在面对一个复杂的电子系统设计时,首先需要对问题进行明确定义。例如,设计一个自动售货机控制系统时,需要定义哪些输入信号(如硬币、按钮),以及对应的输出响应(如释放商品、找零)。布尔代数在这里可以作为一种强有力的建模工具,将复杂的逻辑关系简化为布尔表达式。
布尔建模的首要步骤是识别所有的逻辑变量,并确定它们之间的逻辑关系。布尔变量通常代表系统中的二元状态,如“开/关”、“是/否”。这些变量可以通过布尔运算符连接起来形成布尔表达式,描述系统的行为。在售货机案例中,如果有一个硬币传感器输入(C),和一个选择按钮输入(S),同时还有一个释放商品的输出(O),则布尔建模可以描述为:
```
O = C AND S
```
### 5.1.2 布尔方程的求解过程
布尔方程的求解涉及到布尔代数的定律和定理。以售货机为例,如果想要设计一个可以选择多个商品的系统,可以通过添加更多的布尔变量和方程来扩展模型。例如,如果售货机有三个选择按钮分别为S1, S2, S3,对应的释放商品输出为O1, O2, O3,则系统描述的布尔方程组可以是:
```
O1 = C AND S1
O2 = C AND S2
O3 = C AND S3
```
如果希望在硬币投入后任选一个商品,可以使用OR运算符来简化布尔方程组:
```
O = C AND (S1 OR S2 OR S3)
```
通过布尔代数的恒等式,如分配律、结合律、德摩根定律等,可以进一步优化方程,降低硬件实现的复杂性。
## 5.2 实践案例:从理论到实际电路的转换
### 5.2.1 综合逻辑电路设计案例
将布尔方程转换为实际电路设计需要对电路元件有深入的了解。上一节中描述的自动售货机控制逻辑可以通过一系列逻辑门来实现。具体来说,每个AND门对应一个商品的释放逻辑,而一个OR门可以用来合并多个选择信号。
电路的绘制从绘制逻辑门符号开始,之后再转换为具体的电子元件,如晶体管等。这一步骤需要考虑实际元件的电气特性和性能,如延迟、功耗等。
为了实现电路,我们可以使用硬件描述语言(HDL),如VHDL或Verilog来编写代码。下面是Verilog代码的一个简单示例:
```verilog
module vending_machine(
input wire coin, // 硬币输入信号
input wire select1, select2, select3, // 选择按钮输入信号
output wire release1, release2, release3 // 商品释放信号
);
// 商品释放的逻辑控制
assign release1 = coin & select1;
assign release2 = coin & select2;
assign release3 = coin & select3;
endmodule
```
### 5.2.2 软件仿真与硬件实现的对比分析
在实际电路设计之前,软件仿真提供了一个检验电路逻辑的平台。使用如ModelSim这类仿真工具,可以验证逻辑功能的正确性,检查信号之间是否存在潜在的逻辑冲突。通过仿真,我们可以对设计进行优化,确保无逻辑错误后再进行实际硬件的搭建。
一旦仿真通过,接下来就是硬件实现阶段。这通常涉及到使用FPGA或ASIC将设计实际化。在硬件实现过程中,工程师需要考虑更多的实际因素,例如信号的时序和同步问题、电压水平和功率消耗,以及电路的稳定性等。
## 5.3 教学与研究中的融合应用
### 5.3.1 教学中的逻辑电路实验设计
在电子工程的教学中,布尔代数和逻辑门的学习往往通过实验来加深理解。例如,可以设计一个简单的实验,让学生用逻辑门搭建一个加法器电路,并通过实际的电路操作来观察布尔代数的运算结果。这样的实验能够提高学生对于理论知识的兴趣,并帮助他们更直观地理解抽象的概念。
实验还可以在计算机上使用仿真软件进行。学生可以先在软件中搭建电路,然后观察和分析电路的行为,无需担心物理元件的限制或成本问题。这种方式为学生提供了自由实验和探索的空间。
### 5.3.2 在电子工程研究中的创新应用
在电子工程研究领域,布尔代数和逻辑门的概念可以被扩展到更加前沿和创新的应用中。例如,在量子计算的研究中,布尔逻辑门的概念可以被转化为量子逻辑门,用于实现量子比特的控制和操作。此外,在人工智能领域,布尔代数可以用于优化神经网络的设计,通过布尔表达式简化神经网络结构,从而提高算法的效率。
布尔代数在这些领域中的应用,不仅要求工程师和研究人员具备深厚的理论基础,还需要他们不断探索和创新,将传统的理论应用到新的技术和问题解决方案中。
布尔代数与逻辑门的结合案例分析向我们展示了理论知识如何被应用在实际问题解决中。从问题定义到电路设计,再到硬件的实现和教学应用,布尔代数和逻辑门始终是电子工程领域不可或缺的工具。通过具体案例,我们不仅验证了布尔代数的实用性,也为进一步的研究和创新奠定了基础。
# 6. 数字电路中的布尔代数与逻辑门优化
## 6.1 布尔代数的优化策略
布尔代数提供了一套理论工具,使我们能够通过优化逻辑表达式来简化数字电路的设计。优化过程包括消除冗余的逻辑门、合并同类项和简化表达式。这一优化策略在减少硬件成本、降低功耗和提高电路性能方面发挥着关键作用。
### 6.1.1 布尔代数优化的步骤
1. **表达式的标准化**:将所有逻辑表达式转换为标准形式,如与或非(AND-OR-NOT)表达式。
2. **简化表达式**:使用布尔代数的规则如德摩根定理、结合律等来简化表达式。
3. **消除冗余项**:找出并消除在布尔表达式中的冗余项,以减少所需的逻辑门数量。
4. **合并同类项**:通过识别并合并表达式中的相似项,来进一步简化电路。
### 6.1.2 优化示例
例如,考虑一个布尔函数 F = AB + AB'C + A'BC。这个表达式可以通过布尔代数的规则进行简化:
- 应用分配律:F = AB + AB'C + A'BC = AB(1) + A'C(B) + A'BC
- 应用恒等律:F = AB + A'BC
- 应用吸收律:F = AB + BC
最终,我们通过应用布尔代数的规则,将原始表达式简化为仅包含两个与门的表达式。
### 6.1.3 优化工具和软件
在现代电路设计中,为了自动化上述过程,设计人员常用到优化工具和软件。例如,使用逻辑合成软件如Logisim和Quartus Prime可以执行自动化的布尔优化,生成最小化电路设计。
## 6.2 逻辑门电路的优化方法
逻辑门的优化不仅限于布尔代数层面,还涉及到物理实现层面。电路设计者会采取一系列策略,以确保电路在实际应用中能够高效运行。
### 6.2.1 逻辑门的重排列
通过重新排列逻辑门的顺序,可以最小化延迟和扇出问题。在设计电路时,我们应该考虑到逻辑门的输出驱动能力,并适当地安排它们,以确保信号在到达目的地之前不会衰减或延迟过多。
### 6.2.2 逻辑门的层次化设计
将复杂的逻辑电路分层,可以优化电路的可读性和可维护性。这涉及将电路逻辑分成多个模块,每个模块仅关注于完成特定的功能。这样做可以减少电路整体的复杂性,并有助于在设计和故障排除过程中进行局部优化。
### 6.2.3 使用查找表(LUT)技术
在一些先进的数字电路设计中,查找表(LUT)技术被用来替代传统的逻辑门。LUT可以实现任意的布尔函数,并且对于复杂函数的实现效率更高。在FPGA(现场可编程门阵列)中,LUT是实现可编程逻辑的基础。
通过上述章节的讨论,我们深入理解了布尔代数和逻辑门在数字电路设计中的优化方法。从布尔代数的简化到逻辑门的物理优化,再到使用现代工具和技术,每一步都是确保电路设计达到高性能、高可靠性和高效率的关键。这些优化手段在现代电子系统设计中扮演着不可或缺的角色,对于提升电路性能、降低成本有着显著效果。
0
0






