统计学的基石：理解p值在假设检验中的挑战与应用


# 摘要
统计学是数据分析的基石，而假设检验则是统计学中用于推断总体参数的关键技术。本文深入探讨了假设检验的基础知识，并详细阐述了p值的定义、计算以及在各种统计检验中的应用。通过案例分析，本文揭示了p值误用的常见问题并提出了解决策略。此外，本文还结合实际数据集，展示如何进行p值分析，提供了数据选择、预处理和结果解释的实用指南，旨在提高研究者对p值概念的理解和应用能力，确保统计数据的准确性和可靠性。

# 关键字
统计学；假设检验；p值；误用策略；数据集；分析实践

参考资源链接：[参数检验：验证零件长度与次品率假设](https://wenku.csdn.net/doc/1yr3up2ihy?spm=1055.2635.3001.10343)
# 1. 统计学与假设检验基础

统计学是数据分析的基石，而假设检验则是统计学中不可或缺的一部分。在本章节中，我们将探讨统计学的基本原理，并逐步深入到假设检验的核心概念。我们将从数据的分布特性讲起，解析数据集在不同条件下的行为表现，并介绍如何基于数据样本推断总体参数。通过假设检验，我们能够对实验或观察到的数据进行科学性的判断，比如确定一种药物是否对治疗特定疾病有效，或者一个新算法是否比现有的算法性能更好。

为了更好地理解假设检验，我们还将讨论以下子话题：

## 1.1 统计推断的类型
统计推断分为参数估计和假设检验两大类。参数估计是基于样本数据对总体参数进行估计的过程，而假设检验则是对样本数据是否支持某一特定假设做出判断。我们将探讨这两种推断方法的区别以及它们在实际研究中的应用。

## 1.2 假设检验的基本步骤
一个典型的假设检验包含以下几个基本步骤：建立零假设和备择假设、选择检验统计量、确定显著性水平以及做出统计决策。在本章中，我们将一一解析这些步骤，并说明它们对于整个检验过程的重要性。

## 1.3 错误类型和显著性水平
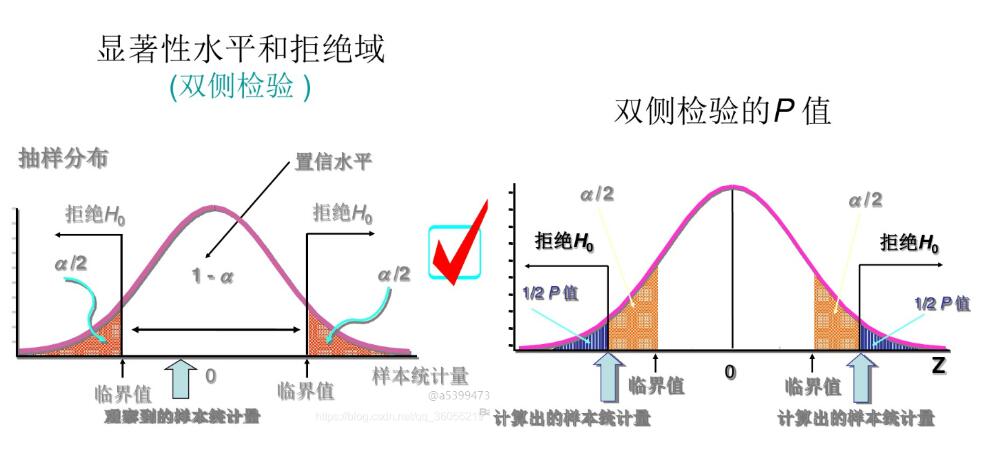
在假设检验中，我们会遇到两类错误：第一类错误和第二类错误。我们将讨论在什么情况下会产生这些错误，并引入显著性水平的概念。显著性水平是控制第一类错误发生概率的一个阈值，它在假设检验中起着决定性作用。此外，我们还将分析如何根据研究目的和数据特点选择合适的显著性水平。

本章节的内容为读者们提供了统计学与假设检验的坚实基础，为进一步学习和理解p值及其在统计检验中的应用打下关键的第一步。

# 2. 深入理解p值的含义与计算

### 2.1 p值的统计学定义
#### 2.1.1 假设检验与p值的关系
在统计学中，假设检验是一个用来决定样本数据是否足够证据拒绝一个关于总体参数的零假设的过程。p值是这一过程中的核心概念，它是在零假设为真的条件下，观察到的统计量或更极端情况出现的概率。p值提供了一种度量，帮助我们判断实验结果是偶然发生的还是可能反映了潜在的真实效应。

#### 2.1.2 p值在统计推断中的角色
p值使我们能够量化证据的强度来反驳零假设。一个较小的p值意味着观察到的数据在零假设为真的情况下出现的概率很小，从而提供了拒绝零假设的强有力证据。通常，如果我们设定的显著性水平为α（如0.05），那么当p值小于α时，我们会拒绝零假设。

### 2.2 计算p值的方法
#### 2.2.1 理论分布的p值计算
在某些情况下，我们可以使用理论分布来计算p值。例如，在z检验和t检验中，我们可以利用标准正态分布和t分布来确定p值。这需要我们找到一个与观察到的统计量相对应的累积分布函数值，然后计算出更极端情况下的概率。

#### 2.2.2 实际数据集的p值计算技巧
对于非标准的情况，我们可能需要利用计算机软件来进行模拟或者数值方法来计算p值。例如，当样本量较大或者总体分布未知时，可以使用自助法（bootstrap）或蒙特卡洛模拟等技术来近似p值。

### 2.3 p值的计算实践

#### 2.3.1 使用统计软件计算p值
许多统计软件提供了计算p值的功能，例如R语言和Python的SciPy库。下面以R语言为例，展示如何使用R计算t检验的p值。

# 假设x和y为两个样本数据集
x <- rnorm(20, mean=5)
y <- rnorm(20, mean=5.5)

# 使用t.test函数进行t检验，并获取p值
result <- t.test(x, y, var.equal=TRUE)

# 输出p值
result$p.value

#### 2.3.2 p值计算逻辑分析
在上述R代码中，`rnorm` 函数生成了两个正态分布的样本数据集x和y。`t.test` 函数执行了一个双样本t检验，并且通过设置`var.equal=TRUE`假定两个样本具有相同的方差。这个函数的输出包含了p值，它表示在两个样本均值相等的零假设为真的前提下，观察到当前统计量或更极端情况的概率。

#### 2.3.3 参数说明
在使用`t.test`函数时，有几个重要的参数需要注意：
- `x` 和 `y`：参与检验的两个样本数据集。
- `var.equal`：一个布尔值，用于指定是否假定两个样本具有相同的方差（当设为TRUE时）。

通过这个示例，我们可以看到在实际数据集上如何进行p值的计算，并且如何利用统计软件来辅助我们的分析工作。

在本章节的后续部分中，我们将探讨p值在不同统计检验中的应用，并通过案例分析来深入理解p值的实际意义和计算方法。

# 3. p值在不同统计检验中的应用案例
## 3.1 t检验中的p值应用
### 3.1.1 单样本t检验的p值分析

在单样本t检验中，p值是用于评估样本均值与一个已知均值之间的差异是否统计显著的指标。我们通常使用t值和相应的自由度（df）来查找p值。如果p值小于事先设定的显著性水平（通常为0.05或0.01），则我们拒绝原假设（H0），表明样本均值与总体均值存在显著差异。

**案例分析：**

假设我们正在研究一项新教学方法对学生成绩的影响。我们选择了一个班级作为样本，并记录了学生在使用新方法前后的成绩。我们假设在新方法前学生的平均成绩