MATLAB次方计算在汽车工程中的应用：深入解析车辆动力学和控制系统的数学原理

# 1. MATLAB基础**

MATLAB 是一种用于技术计算的高级编程语言。它提供了广泛的工具和函数，使工程师能够高效地解决复杂问题。MATLAB 在汽车工程中得到了广泛的应用，从车辆动力学建模到控制系统设计。

MATLAB 的核心优势在于其易用性和可扩展性。它具有直观的语法和丰富的库，使工程师能够快速开发和部署解决方案。此外，MATLAB 与其他软件工具和硬件设备的集成使其成为汽车工程中多学科协作的理想平台。

# 2. MATLAB在汽车工程中的应用

MATLAB在汽车工程中扮演着至关重要的角色，为工程师提供了一套强大的工具，用于车辆动力学建模、控制系统设计、仿真和数据分析。

### 2.1 车辆动力学建模

#### 2.1.1 运动方程

车辆动力学建模的基础是运动方程，这些方程描述了车辆在各个方向上的运动。MATLAB提供了一系列函数来求解这些方程，包括：

- `ode45`：用于求解常微分方程。
- `ode23tb`：用于求解刚性微分方程。
- `ode15s`：用于求解非刚性微分方程。

**代码块：**

% 定义车辆参数
m = 1500; % 质量 (kg)
Iz = 2500; % 惯性矩 (kg-m^2)
lf = 1.2; % 前轮轴距 (m)
lr = 1.5; % 后轮轴距 (m)
Cf = 150000; % 前轮侧向刚度 (N/rad)
Cr = 100000; % 后轮侧向刚度 (N/rad)

% 定义状态变量
x = [0; 0; 0; 0]; % [x; y; theta; v]

% 定义时间范围
t_span = [0, 10];

% 求解运动方程
[t, y] = ode45(@(t, x) vehicle_dynamics(t, x, m, Iz, lf, lr, Cf, Cr), t_span, x);

% 绘制结果
plot(t, y(:, 1), 'b', t, y(:, 2), 'r', t, y(:, 3), 'g', t, y(:, 4), 'k');
legend('x', 'y', 'theta', 'v');
xlabel('时间 (s)');
ylabel('状态变量');

**逻辑分析：**

此代码块使用`ode45`求解车辆动力学运动方程。它定义了车辆参数、状态变量和时间范围。`vehicle_dynamics`函数计算运动方程的右端。结果绘制为位置、速度、角度和角速度随时间的函数。

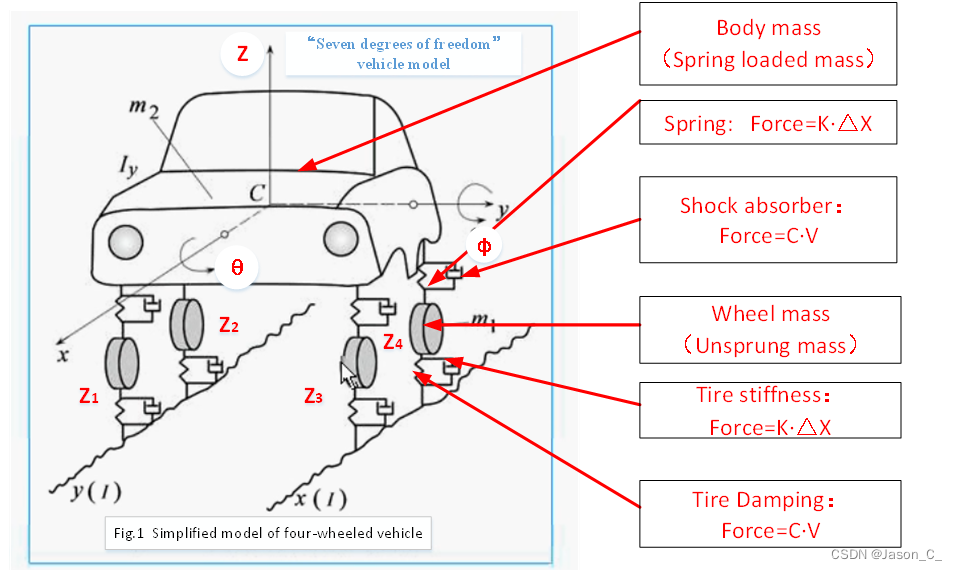
#### 2.1.2 悬架系统建模

MATLAB还可用于对悬架系统进行建模，悬架系统负责吸收道路不平整引起的冲击。悬架系统模型可以包括弹簧、阻尼器和连杆。

**代码块：**

% 定义悬架参数
k = 10000; % 弹簧刚度 (N/m)
c = 100; % 阻尼系数 (N-s/m)

% 定义状态变量
x = [0; 0]; % [z; v]

% 定义时间范围
t_span = [0, 1];

% 求解悬架方程
[t, y] = ode23tb(@(t, x) suspension_dynamics(t, x, k, c), t_span, x);

% 绘制结果
plot(t, y(:, 1), 'b', t, y(:, 2), 'r');
legend('z', 'v');
xlabel('时间 (s)');
ylabel('状态变量');

**逻辑分析：**

此代码块使用`ode23tb`求解悬架系统方程。它定义了悬架参数、状态变量和时间范围。`suspension_dynamics`函数计算悬架方程的右端。结果绘制为车身位移和速度随时间的函数。

### 2.2 控制系统设计

#### 2.2.1 PID控制

PID控制是一种经典的控制算法，用于将实际输出与期望输出进行比较，并根据误差生成控制信号。MATLAB提供了一个`pid`函数来设计和实现PID控制器。

**代码块：**

% 定义PID参数
Kp = 1; % 比例增益
Ki = 0.1; % 积分增益
Kd = 0.01; % 微分增益

% 创建PID控制器
pid_controller = pid(Kp, Ki, Kd);

% 定义参考信号
r = 1; % 期望输出

% 定义时间范围
t_span = [0, 10];

% 求解控制系统方程
[t, y] = ode45(@(t, x) pid_control(t, x, r, pid_controller), t_span, [0]);

% 绘制结果
plot(t, y, 'b', t, r, 'r');
legend('实际输出', '期望输出');
xlabel('时间 (s)');
ylabel('输出');

**逻辑分析：**

此代码块使用`ode45`求解PID控制系统方程。它定义了PID参数、参考信号和时间范围。`pid_control`函数计算控制系统方程的右端。结果绘制为实际输出和期望输出随时间的函数。

#### 2.2.2 状态空间控制

状态空间控制是一种高级控制技术，它使用状态方程来描述系统的动态行为。MATLAB提供了一系列函数来设计和实现状态空间控制器，包括：

- `lqr`：用于设计线性二次调节器 (LQR)。
- `place`：用于设计极点配置控制器。
- `acker`：用于设计阿克曼控制器。

# 3. MATLAB在汽车工程中的实践

### 3.1 车辆仿真

#### 3.1.1 Simulink建模

Simulink是MATLAB中用于多域建模和仿真的图形化环境。它提供了一个直观的拖放式界面，用于创建复杂系统的块状图模型。在汽车工程中，Simulink广泛用于车辆动力学、控制系统和电气系统建模。

**步骤：**

1. 打开Simulink并创建一个新模型。
2. 从Simulink库中拖放所需的模块到模型中。
3. 连接模块以创建系统模型。
4. 设置模型参数和仿真参数。
5. 运行仿真并分析结果。

**示例：**

以下代码块展示了一个使用Simulink建模的简单车辆动力学模型：

% 创建 Simulink 模型
model = simulink.Model('VehicleDynami