【Hadoop快照与数据一致性】：确保数据安全的关键技术

# 1. Hadoop快照的基础概念

Hadoop快照是数据备份与恢复策略中的一个重要组成部分。简而言之，快照就是特定时间点上文件系统的副本。对于Hadoop这样的大数据平台，它允许在不停机的情况下，对数据进行瞬间备份。在本章中，我们将探讨快照的概念，并分析其在Hadoop系统中的作用和优势。

在Hadoop生态系统中，快照技术特别适用于大数据分析、机器学习和数据仓库场景。它可以在数据操作过程中提供数据一致性保证，这对于维护企业数据安全与可靠性至关重要。

## 1.1 快照的工作原理
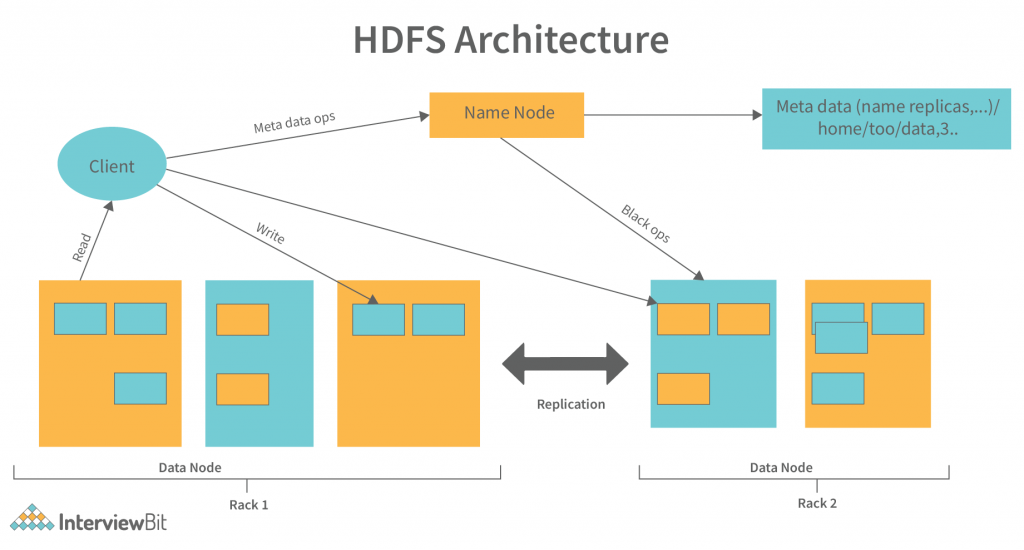
快照通过创建存储在HDFS（Hadoop Distributed File System）中数据块的引用拷贝来工作。当创建快照时，系统记录下当前文件系统的状态，并在必要时利用这些引用拷贝恢复文件系统到之前的状态。为了保证操作的高效性，快照只复制文件元数据的变化，而不是整个文件的数据。

# 创建快照的示例命令
hdfs dfsadmin -allowSnapshot /path/to/directory

这条命令允许对指定目录创建快照，路径`/path/to/directory`即为要创建快照的目录。

## 1.2 快照的应用场景
在Hadoop中，快照不仅仅用于备份与恢复数据，它还可以用于数据版本管理、灾难恢复计划和数据挖掘等多种场景。由于快照是存储空间高效的数据保护机制，它为大数据运维人员提供了一个强有力的工具。

通过理解这些基础概念，IT专业人员能够更好地掌握Hadoop快照技术，并将其有效融入到数据管理和恢复策略中。接下来的章节将深入探讨数据一致性及其在Hadoop中的理论基础，以及快照与数据一致性的协同工作。

# 2. Hadoop数据一致性的理论基础

## 2.1 数据一致性的定义与重要性

### 2.1.1 数据一致性的基本概念

数据一致性是指在分布式系统中，多个数据副本之间保持相同的状态。在Hadoop这样的分布式存储系统中，数据一致性是保障数据可靠性和正确性的核心。数据一致性的定义基于ACID属性（原子性、一致性、隔离性、持久性），但分布式系统由于其复杂性，在实现上很难完全满足ACID的所有特性，因此，Hadoop采用了 BASE（基本可用、软状态、最终一致性）模型，以适应大规模分布式环境下的实际需求。

在Hadoop生态中，数据一致性尤为重要，因为Hadoop主要被用于存储和处理大量数据。如果数据不一致，可能会导致分析结果出现偏差，甚至导致整个系统的决策错误。因此，确保数据一致性是Hadoop系统设计和运行时必须考虑的关键因素。

### 2.1.2 一致性级别及其在Hadoop中的应用

在Hadoop中，数据的一致性水平可以通过配置不同的复制策略来调整。Hadoop提供了多个一致性级别，如“最终一致性”、“强一致性”等，这些级别定义了在读取数据时数据状态的一致性要求。

例如，在Hadoop HDFS中，通过配置不同的一致性级别，可以在读取数据时获取到最新的数据状态，或是允许读取到过期但稳定的快照。系统管理员可以根据业务场景对数据一致性的要求，选择适当的配置，以满足业务的性能和一致性需求。

## 2.2 Hadoop中的数据复制机制

### 2.2.1 HDFS的数据复制原理

Hadoop分布式文件系统（HDFS）的核心设计理念之一就是数据复制。通过在多个数据节点（DataNode）上存储数据的多个副本，HDFS实现了数据的高可用性和容错性。

HDFS数据复制的基本原理是，当文件写入HDFS时，它被分割成数据块（默认大小为128MB），这些数据块会被复制到集群的不同DataNode上。默认情况下，每个数据块会有三个副本，一个放在NameNode指定的主副本（Primary副本）位置，其他两个放在其他不同的DataNode上。这种复制机制大大提高了系统的可靠性，即便有节点失效，系统也能保证数据不丢失。

### 2.2.2 复制策略对一致性的影响

复制策略在Hadoop中对于数据一致性的影响至关重要。Hadoop提供了可配置的复制策略，允许用户根据实际需要调整副本数量以及副本间的同步频率。

例如，如果需要较高的数据一致性，可以增加副本之间的同步频率，使得数据状态的同步更加及时。相反，如果对一致性要求不高，但需要提高读写性能，则可以适当降低副本间的同步频率，这样可以减少网络和磁盘I/O的开销。然而，这可能会导致在读取数据时无法获得最新的数据状态，即出现短暂的一致性问题。

## 2.3 一致性模型在Hadoop中的实现

### 2.3.1 Hadoop的一致性模型概述

Hadoop采用的一致性模型主要基于“最终一致性”模型。在这种模型下，Hadoop保证系统最终会达到一个一致的状态，但并不保证立即一致。这意味着在某些时刻，数据的多个副本可能并不完全相同，但随着时间的推移，所有的副本最终会变得一致。

为了实现这一模型，Hadoop中的NameNode和DataNode协同工作，确保数据块的副本管理遵循一致性原则。Hadoop通过内部的“心跳”机制和数据块的校验过程来监控数据副本的状态，保证副本之间最终保持一致。

### 2.3.2 如何在Hadoop环境中维护一致性

为了在Hadoop环境中维护数据一致性，系统管理员需要进行一系列的配置和监控工作。首先，需要合理配置HDFS的数据复制因子，以确保有足够的副本以应对节点故障。其次，可以通过调整副本间的同步策略，使得数据状态尽快同步，减少一致性问题的发生。

此外，对于特定的数据处理应用，可以通过编程接口，实现应用层的数据一致性保障机制。例如，通过在应用层面实现读写时的校验和检查，或者采用事务管理来确保数据操作的一致性。在某些情况下，还可以结合外部一致性保障工具，如Apache ZooKeeper，来实现更加复杂的一致性管理策略。

# 3. Hadoop快照技术的实践应用

## 3.1 快照技术的工作原理

### 3.1.1 快照的创建与管理

Hadoop中的快照是一种数据保护和备份机制，它允许系统管理员创建文件系统的一个只读副本，而不影响原始数据的读写操作。创建快照的目的是为了在数据出现错误或损坏时能够迅速恢复到一个已知的正确状态。

在Hadoop中，快照的创建与管理通常是通过HDFS的命令行工具进行的，使用以下命令可以创建一个快照：

hdfs dfs -createSnapshot <path-to-directory> <snapshot-name>

这条命令会创建一个名为`<snapshot-name>`的快照，该快照包含了指定目录`<path-to-directory>`的数据。创建快照的用户需要具备相应的HDFS目录写权限。一旦快照被创建，HDFS会保存所有与原始目录不同的文件和块的元数据。

快照管理主要包括查看、删除和恢复快照等操作。HDFS提供了相关的命令行工具来执行这些操作：

- 查看快照列表：

hdfs lsSnapshottableDir <path-to-directory>

- 删除快照：

hdfs dfs -deleteSnapshot <path-to-directory> <snapshot-name>

- 恢复快照：

hdfs dfs -restoreSnapshot <path-to-directory> <snapshot-name>

需要注意的是，快照不包含文件系统的实际数据块，仅