【Go Cond与互斥锁（Mutex）协同】：构建无懈可击的并发逻辑（并发逻辑构建手册）

# 1. Go并发模型基础

Go语言的并发模型是其一大特色，它提供了轻量级的goroutine，以及用于协调和同步的channel和各种同步原语。在这一章中，我们将简单回顾并发的基本概念，并探索Go语言中的并发模型如何被实现和使用。

Go的并发模型基于CSP（Communicating Sequential Processes）理论，该理论强调通过消息传递来进行并发程序设计。每一个并发执行的单元被称为goroutine，它们通过channel进行通信。goroutine相较于传统的线程更加轻量，启动和管理成本更低，可以创建成千上万个goroutine而不会对系统资源造成过大压力。

我们将通过基础示例来展示如何创建goroutine以及如何使用channel来实现线程安全的消息传递。这种编程模型将为读者展示Go语言并发的简单和高效。

package main

import "fmt"

// 示例函数，用于goroutine
func sayHello(name string) {
    fmt.Println("Hello", name)
}

func main() {
    // 创建一个goroutine并发执行sayHello
    go sayHello("world")
    // 主goroutine继续执行其他任务
    fmt.Println("main goroutine")
}

以上代码展示了在Go中如何启动一个goroutine，主函数在打印完"main goroutine"后可能会立即结束，但由于有另一个goroutine正在运行，程序会等待它完成后再退出。这种并发控制机制是Go语言并发模型的基石。

在后续章节中，我们将深入探讨Go语言提供的同步原语，如Mutex和Cond，以及如何高效地管理和优化并发程序，为构建健壮的并发系统打下坚实的基础。

# 2. 深入理解Cond与Mutex

## 2.1 Mutex的基本原理和使用
### 2.1.1 Mutex的类型和状态

在Go语言中，`sync.Mutex` 是一个互斥锁，它提供了一种机制来保证代码片段在并发执行时的互斥访问。Mutex有两种状态：加锁（locked）和解锁（unlocked）。它保证同一时间只有一个goroutine能够访问被保护的资源。

var mu sync.Mutex

在互斥锁的使用中，有两种主要的方法：

- `Lock()`：调用该方法会将锁置于锁定状态，如果有其他goroutine已经持有了锁，那么调用者将会阻塞，直到锁被释放。
- `Unlock()`：调用该方法会将锁置于未锁定状态，如果有其他goroutine正在等待该锁的释放，那么它们中的一个将会被唤醒并获取锁。

### 2.1.2 Mutex在并发中的作用

在并发编程中，`sync.Mutex` 起到了至关重要的作用。通过它的加锁和解锁机制，可以避免多个goroutine同时修改同一资源导致的数据不一致问题。

func main() {
    mu.Lock()
    defer mu.Unlock()
    // 临界区代码
    fmt.Println("Critical section")
}

在这段代码中，我们使用`mu.Lock()`来锁定一个临界区，任何尝试进入这个临界区的其他goroutine都将被阻塞，直到我们调用`mu.Unlock()`解锁。临界区通常包含对共享资源的操作，通过互斥锁来保证资源访问的原子性。

## 2.2 Cond的同步机制解析
### 2.2.1 Cond的创建和使用方法

条件变量是一种同步原语，它允许一个或多个goroutine在满足特定条件之前暂停执行，并且在该条件变为真时由其他goroutine唤醒。在Go中，`sync.Cond` 提供了条件变量的实现。

var cond = sync.NewCond(&sync.Mutex{})

创建一个`sync.Cond`时，需要传递一个指向已存在的互斥锁的指针。互斥锁用来保护条件变量的状态，确保在调用等待和通知方法时的线程安全。

使用条件变量的步骤通常如下：

1. 获取条件变量关联的互斥锁。
2. 等待条件变量，释放互斥锁并阻塞当前goroutine。
3. 被其他goroutine唤醒后，重新获取互斥锁。
4. 重复检查条件是否满足，如果满足，继续执行。
5. 完成后，解锁互斥锁。

### 2.2.2 Cond与channels的区别

在Go中，`channels` 和 `sync.Cond` 都可以用来同步goroutine，但是它们在使用上有本质的区别：

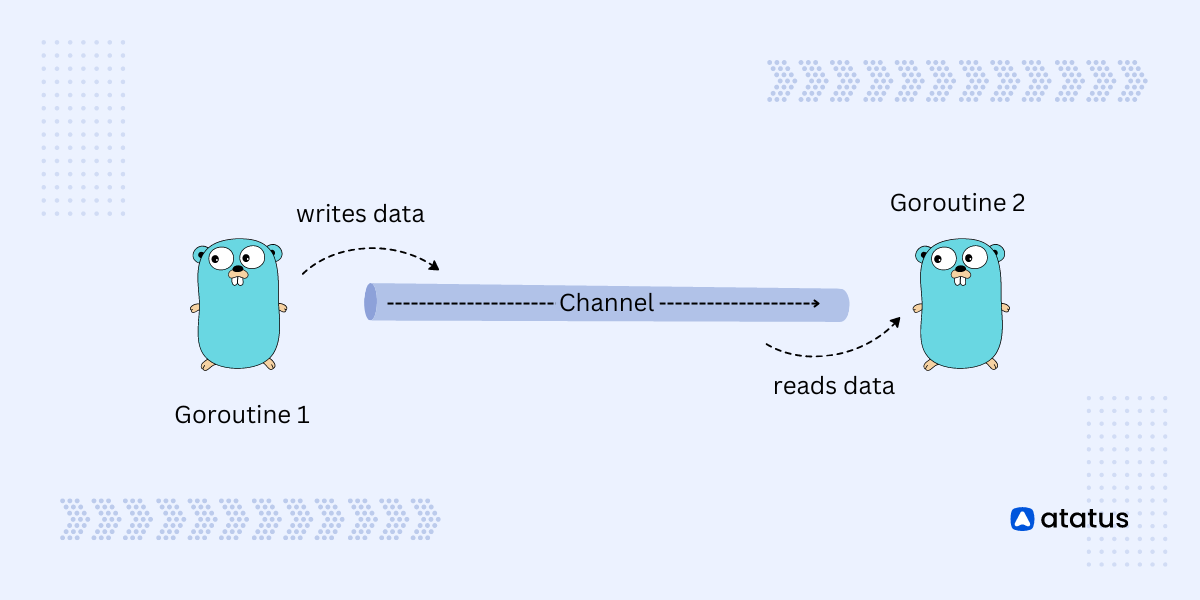
- Channels：它们是基于发送和接收消息的机制，通常用于goroutine间的直接通信。
- Cond：它们提供了一种等待和通知的机制，用于单个或多个goroutine在满足某个条件前的暂停。

尽管在功能上有重叠，但在并发设计时选择使用哪种方式取决于具体的应用场景。例如，当你希望有多个goroutine等待同一个条件时，使用条件变量更为直观。

## 2.3 Cond与Mutex的协同工作原理
### 2.3.1 阻塞与唤醒机制的交互

`sync.Cond`的阻塞与唤醒机制与`sync.Mutex`紧密相关。当一个goroutine调用`cond.Wait()`方法时，它会首先释放`sync.Cond`关联的互斥锁，然后进入等待状态。在这个过程中，其他的goroutine可以获取到这个锁并执行临界区中的代码。当条件变得满足，调用`cond.Signal()`或`cond.Broadcast()`可以唤醒等待中的一个或所有goroutine。

阻塞和唤醒机制是这样工作的：

1. 当某个goroutine需要等待一个条件时，它调用`cond.Wait()`方法。
2. `cond.Wait()`方法会释放互斥锁，并使得当前goroutine进入等待状态。
3. 当其他goroutine调用`cond.Signal()`或`cond.Broadcast()`时，之前等待的goroutine会被唤醒。
4. 唤醒的goroutine会尝试重新获取互斥锁，一旦成功，它就会继续执行临界区中的代码。

### 2.3.2 条件变量在资源管理中的应用

条件变量在资源管理中有广泛的应用，如在资源限制、任务调度、状态监听等场景中都可看到条件变量的身影。在资源管理场景中，一个或多个生产者goroutine会生成任务并将其放入队列中，而消费者goroutine则从队列中取出任务并执行。在队列为空时，消费者需要等待任务的到来。

下面是一个使用条件变量管理资源的简单示例：

func worker(c *sync.Cond) {
    c.L.Lock()
    for workQueue.Empty() {
        c.Wait() // 等待条件变量
    }
    task := workQueue.Pop() // 弹出一个任务
    c.L.Unlock()
    execute(task)
}

func main() {
    cond := sync.NewCond(&sync.Mutex{})
    // 创建并启动工作goroutine
    go worker(cond)
    // 生产任务并通知等待的消费者
    func() {
        for {
            cond.L.Lock()
            workQueue.Push(newTask())
            cond.Signal() // 通知等待的消费者
            cond.L.Unlock()
            // 等待下一次任务的生成
        }
    }()
}

在这个例子中，消费者goroutine在任务队列为空时通过`cond.Wait()`方法阻塞并等待。生产者goroutine在添加任务到队列后调用`cond.Signal()`唤醒一个等待的消费者goroutine，这样就保证了任务队列不会被一个空队列阻塞，同时确保消费者goroutine能够有效利用资源，按需执行任务。

以上章节内容展示了Mutex和Cond的基础使用方法和原理，以及它们在并发编程中的协同工作原理。通过细致的分析，我们对这两个并发控制工具有了深入的认识，这将为进一步探索复杂的并发场景打下坚实的基础。

# 3. Cond与Mutex的实践应用

在本章中，我们将深入探讨在实际开发中如何应用Cond和Mutex来解决并发编程中遇到的问题。这不仅需要理论知识，更需要丰富的实践经验来保证代码的健壮性和高效性。

## 3.1 简单的并发场景应用

在并发编程中，基本场景的实现是构建复杂系统的基础。我们将从简单的例子开始，逐步深入理解Cond与Mutex的实战应用。

### 3.1.1 使用Mutex保护共享资源

共享资源的访问是并发编程中需要首先考虑的问题。Mutex（互斥锁）是解决这一问题的关键。以下是使用Mutex保护共享资源的简单代码示例：

package main

import (
	"fmt"
	"sync"
)

var (
	count  int
	counts sync.WaitGroup
	mtx    sync.Mutex
)

func worker() {
	defer counts.Done()
	mtx.Lock()
	count++
	mtx.Unlock()
}

func main() {
	const gr = 100
	counts.Add(gr)
	for i := 0; i < gr; i++ {
		go worker()
	}
	counts.Wait()
	fmt.Println(count)
}

**代码逻辑解读：**
- 我们定义了一个全局的`count`变量和一个`sync.WaitGroup`用于等待所有goroutine完成。
- 在每个工作goroutine中，我们首先调用`mtx.Lock()`来获得锁，这会阻止其他goroutine同时访问`count`变量。
- 增加`count`的值后，通过`mtx.Unlock()`释放锁，从而允许其他goroutine继续执行。
- 在`main`函数中，我们启动了多个goroutine，并在所有goroutine完成后打印出`count`的最终值。

### 3.1.2 利用Cond