【精通经纬度转换】：10大实用技巧详解与案例分析


参考资源链接：[腾讯地图与百度地图经纬度转换算法](https://wenku.csdn.net/doc/c4va87n0da?spm=1055.2635.3001.10343)
# 1. 经纬度转换基础概念解析

在地理信息系统（GIS）和全球定位系统（GPS）中，经纬度转换是一个基本而关键的过程。它指的是将地理坐标系统（GCS）中的球面坐标转换为投影坐标系统（PCS）中的平面坐标，反之亦然。这种转换是处理地理数据不可或缺的一步，尤其是在需要将数据从地球的曲面模型投影到平面地图上的时候。

## 地理坐标系统（GCS）

地理坐标系统，通常基于地球的椭球模型，通过经度和纬度来描述地球表面的位置。经度表示东西位置，而纬度表示南北位置。GCS的主要功能是提供一个全球统一的参照基准。

## 投影坐标系统（PCS）

投影坐标系统将地球的三维曲面映射到二维平面。该过程必然引入了一定的变形，但通过适当的投影方法可以优化某些地理特性（如面积、形状、方向或距离）的保真度。投影类型的选择取决于地图用途和所需的精度。

在第二章，我们将详细探讨WGS84和CGCS2000等地理坐标系统，以及Web Mercator和兰伯特等角圆锥等投影坐标系统，并分析它们之间的转换原理。

# 2. 常见经纬度坐标系统详解

## 2.1 地理坐标系统(GCS)
地理坐标系统（Geographic Coordinate Systems，GCS）是用来定义地球表面上位置的一种坐标系统。GCS基于地球的几何模型，由经线和纬线组成，其关键要素包括本初子午线、赤道以及地球模型（参考椭球体）。

### 2.1.1 WGS84坐标系统
WGS84（World Geodetic System 1984）是目前国际上广泛使用的地理坐标系统，也是全球定位系统（GPS）的基础。它基于一个定义良好的地球模型，使用地球质心为原点，提供全球通用的经纬度坐标。

#### 关键参数：
- **参考椭球体**：WGS84采用的是一个近似于地球形状的旋转椭球体，其长半轴a为6378137米，扁率f为1/298.257223563。
- **原点**：位于地球质心。
- **经度线**：从格林威治本初子午线开始向东、向西分别计算0°到180°。
- **纬度线**：赤道为0°，分别向北和向南计算到90°。

### 2.1.2 CGCS2000坐标系统
CGCS2000（中国大地坐标系统2000）是中国的地理坐标系统，它比之前广泛使用的1954北京坐标系或1980西安坐标系更精确。该系统是基于地壳运动模型，更适用于当前中国大陆的测绘和导航。

#### 关键参数：
- **参考椭球体**：CGCS2000采用的是IAG 1980椭球体。
- **原点**：以地球质心为原点。
- **本初子午线**：位于中国中部，大约在东经117度附近。

### 2.2 投影坐标系统(PCS)
投影坐标系统（Projected Coordinate Systems，PCS）是通过将三维的地理坐标系统转换为二维平面坐标系统而得到的。其目的是为了简化地图制作、进行更加精确的测量计算。常用的投影坐标系统包括Web Mercator投影和兰伯特等角圆锥投影。

### 2.2.1 Web Mercator投影
Web Mercator投影（或称Google投影）是网络地图服务中广泛使用的一种平面投影系统，特别适用于全球或较大区域的地图展示。

#### 特点：
- **等角投影**：保持了方向的相对一致性。
- **比例变化**：距离中心越远，面积变形越大。
- **适合网络地图**：便于进行Web上的地图缩放和叠加。

### 2.2.2 兰伯特等角圆锥投影
兰伯特等角圆锥投影是一种将地球的椭球模型展开成圆锥后投影到平面上的地理投影方法。这种投影方法在区域地图中广泛使用，因为它能较好地保持面积、形状和角度的准确度。

#### 特点：
- **局部等角**：在投影的中央区域，保持了形状和面积的比例。
- **多中心投影**：可有多个标准平行线以适应不同的区域。
- **适合区域地图**：主要用于中小比例尺的地图。

### 2.3 坐标系统之间的转换原理
将GCS和PCS之间的坐标进行转换是空间数据处理中的一个基本操作。这一转换涉及到了复杂的数学计算，通常需要通过一系列几何变换以及数学模型来实现。

### 2.3.1 从GCS到PCS的转换
从地理坐标系统转换到投影坐标系统，通常需要经过以下步骤：
1. 将地理坐标（经纬度）转换为大地坐标。
2. 采用相应的投影方法将大地坐标转换为笛卡尔坐标系中的X、Y、Z坐标。
3. 根据地图显示范围，对X、Y坐标进行缩放和平移。

### 2.3.2 从PCS到GCS的转换
反向转换，即从投影坐标系统转换回地理坐标系统，比前者更为复杂。通常步骤包括：
1. 确定投影坐标所使用的投影方法和相关参数。
2. 对投影坐标进行逆运算，将X、Y坐标转换回大地坐标。
3. 将大地坐标转换为经纬度坐标。

下面是一段简化的伪代码示例，展示了如何使用Python进行经纬度坐标与Web Mercator投影坐标之间的转换：

import math

# 定义一些基本的转换常量
RADIUS_EARTH_M = 6371000
PI = math.pi

def latlon_to_mercator(lat, lon):
    """
    将WGS84经纬度转换为Web Mercator投影坐标。
    lat: 纬度（度）
    lon: 经度（度）
    返回: x, y（米）
    """
    x = lon * RADIUS_EARTH_M * PI / 180.0
    y = math.log(math.tan((90 + lat) * PI / 360.0)) / (PI / 180.0)
    y = y * RADIUS_EARTH_M / 180.0
    return x, y

def mercator_to_latlon(x, y):
    """
    将Web Mercator投影坐标转换回WGS84经纬度坐标。
    x: x坐标（米）
    y: y坐标（米）
    返回: lat, lon（度）
    """
    lon = (x / RADIUS_EARTH_M / PI) * 180.0
    lat = (y / RADIUS_EARTH_M) * 180.0
    lat = 180 / PI * (2 * math.atan(math.exp(lat * PI / 180.0)) - PI / 2)
    return lat, lon

# 示例转换
lat = 39.913818
lon = 116.363625
x, y = latlon_to_mercator(lat, lon)
print(f"Mercator Projection: {x:.2f}, {y:.2f}")

lat, lon = mercator_to_latlon(x, y)
print(f"Latitude & Longitude: {lat:.2f}, {lon:.2f}")

以上代码提供了从WGS84经纬度到Web Mercator投影的转换，反之亦然。这些计算涉及复杂的三角函数和对数运算，借助数学库可以帮助我们简化这些操作。在实际应用中，还需考虑到不同坐标系统之间的偏差和调整，因此实际的转换过程可能会更加复杂。

在本章中，我们详细探讨了地理坐标系统和投影坐标系统的概念和关键参数，并通过Web Mercator投影和兰伯特等角圆锥投影的具体案例，阐述了坐标系统之间的转换原理和步骤。理解这些转换原理是进行精确地图制图和地理数据分析的基础。在接下来的章节中，我们将继续深入探讨经纬度转换的实用技巧，包括使用工具和编程实现的方法。

# 3. 经纬度转换实用技巧

### 3.1 使用坐标转换工具

在日常工作中，面对复杂的坐标转换任务，手动计算既耗时又容易出错。因此，熟练地使用现成的转换工具可以显著提高效率。本节将介绍几种常见的经纬度坐标转换工具及其使用方法。

#### 3.1.1 在线转换工具的使用方法

网络上有众多免费的在线坐标转换工具，用户无需安装任何软件即可使用。以“epsg.io”为例，用户只需访问其网站，输入原始坐标，选择对应的源坐标系统和目标坐标系统，点击转换即可得到结果。

flowchart LR
    A[输入原始坐标] --> B[选择源坐标系统]
    B --> C[选择目标坐标系统]
    C --> D[点击转换]
    D --> E[获得转换结果]

这些在线工具简单易用，适合处理单个数据点的转换，但它们的缺点是转换精度受限于提供工具的服务端，且不适合大批量数据处理。

#### 3.1.2 常用GIS软件的转换功能

除了在线工具外，专业的GIS软件如QGIS和ArcGIS也提供了强大的坐标转换功能。这些软件内嵌了大量坐标系统，并且支持批量转换数据。

在QGIS中，用户可以通过“Vector”菜单下的“Research Tools”找到“Coordinate Capture”工具，进行实时坐标的捕获和转换。而“Project”菜单中的“Project Properties”可以用来设置地图的坐标系统，实现数据在不同坐标系统之间的自动转换。

在ArcGIS中，用户可以通过“Data Management Tools”里的“Projections and Transformations”工具集，执行类似的操作。该软件还支持创建自定义的坐标转换脚本，以适应更复杂的转换需求。

### 3.2 手动计算转换公式

在某些情况下，我们可能无法访问转换工具，或者需要验证转换结果的准确性。这时，掌握一些基本的坐标转换公式和球面三角学知识就显得尤为重要。

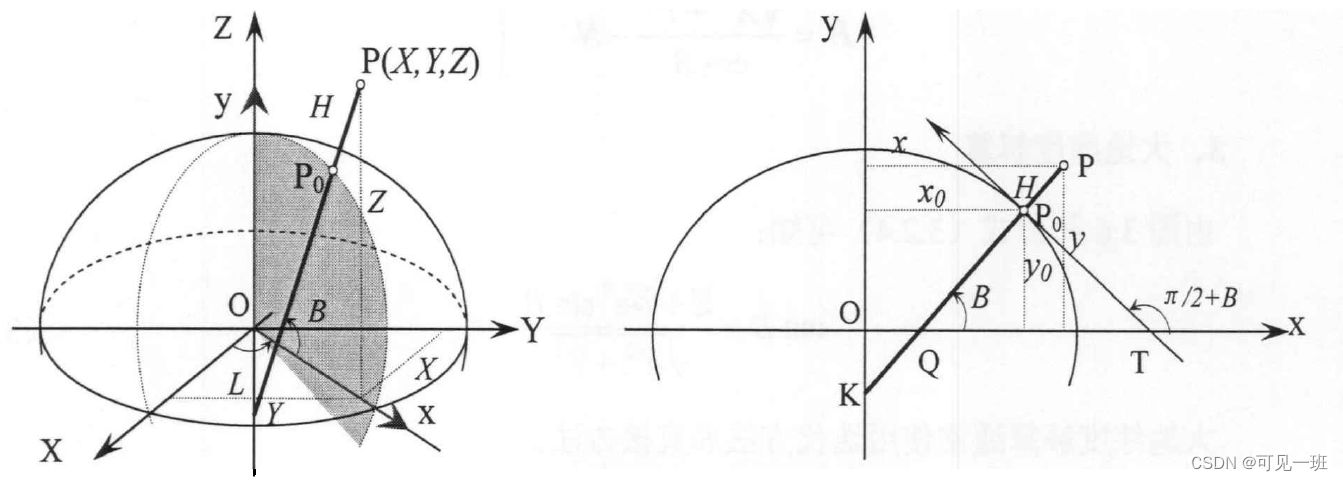
#### 3.2.1 球面三角学在转换中的应用

球面三角学是研究球面上三角形的学科，它提供了一套处理经纬度转换的公式。一个常见的应用是将大地坐标转换为笛卡尔坐标。

假设有一个大地坐标（φ, λ, h），其中φ为纬度，λ为经度，h为高度。其对应的笛卡尔坐标（X, Y, Z）可以通过以下公式获得：

X = (N + h) * cos φ * cos λ
Y = (N + h) * cos φ * sin λ
Z = [(N * (1 - e^2)) + h] * sin φ

这里N是椭球体的卯酉圈曲率半径，e是椭球体的第一偏心率。

#### 3.2.2 坐标转换中的误差处理

在手动计算坐标转换时，不可避免会遇到一些误差。这可能来源于原始数据的精度、计算公式的简化处理，或者数值计算过程中的舍入误差。

为了最小化误差，我们需要：

- 确保使用高精度的原始数据。
- 了解所使用转换公式的适用范围和限制。
- 采用高精度的数值计算方法和足够精确的数值常量。
- 当处理大批量数据时，进行样本测试，分析误差分布，必要时进行误差补偿。

### 3.3 编程实现经纬度转换

在某些自动化应用或者复杂的项目中，我们可能需要通过编程实现经纬度转换。本小节将探讨在编程中实现坐标转换的常用库和自定义转换函数的构建。

#### 3.3.1 常用编程语言中的转换库

目前，多种编程语言中都有成熟的第三方库可以用于处理坐标转换，例如Python中的`pyproj`库、Java中的`Geotools`库，以及.NET中的`ProjNet4GeoAPI`库。

以Python为例，`pyproj`库是Python接口，可以访问PROJ库（一个广泛用于地图投影和坐标转换的库）。用户只需要简单几行代码，即可实现复杂的坐标转换。

from pyproj import Proj, transform

# 定义源和目标坐标系统的proj4字符串
source_crs = "+proj=latlon +datum=WGS84"
target_crs = "+proj=utm +zone=33 +datum=WGS84"

# 创建坐标系统对象
sourceProj = Proj(source_crs)
targetProj = Proj(target_crs)

# 坐标转换
lon, lat = -122.258, 37.842
x, y = transform(sourceProj, targetProj, lon, lat)

print(f"UTM坐标: {x}, {y}")

该库通过`transform`函数，可将经纬度坐标转换为UTM坐标，也可以在其他坐标系统之间进行转换。

#### 3.3.2 实现自定义转换函数的步骤

在某些特定需求下，可能没有现成的库可以使用，这时就需要自己实现转换函数。以Python实现WGS84到GCJ02（中国区特殊处理坐标系统）的转换为例，可以遵循以下步骤：

1. 确定转换算法或方法。在这个例子中，可以采用七参数转换模型。
2. 实现算法中的每个数学步骤。例如，编写函数来计算经度和纬度的偏差。
3. 构建辅助函数来处理重复性的任务，比如将经纬度转换为弧度。

import math

# 定义转换函数
def wgs84_to_gcj02(lat, lon):
    # 定义转换参数
    a = 6378245.0  # 长半轴
    ee = 0.00669342162296594323  # 扁率平方
    dLat = transformLat(lon - 105.0, lat - 35.0)
    dLon = transformLon(lon - 105.0, lat - 35.0)
    radLat = lat / 180.0 * math.pi
    magic = math.sin(radLat)
    magic = 1 - ee * magic * magic
    sqrtMagic = math.sqrt(magic)
    dLat = (dLat * 180.0) / (((a * (1 - ee)) / (magic * sqrtMagic)) * 3600.0)
    dLon = (dLon * 180.0) / (a / sqrtMagic * math.cos(radLat) * 3600.0)
    mgLat = lat + dLat
    mgLon = lon + dLon
    return mgLat, mgLon

# 辅助函数
def transformLat(x, y):
    ret = -100.0 + 2.0 * x + 3.0 * y + 0.2 * y * y + 0.1 * x * y + 0.2 * math.sqrt(abs(x))
    ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
    ret += (20.0 * math.sin(y * math.pi) + 40.0 * math.sin(y / 3.0 * math.pi)) * 2.0 / 3.0
    ret += (160.0 * math.sin(y / 12.0 * math.pi) + 320 * math.sin(y * math.pi / 30.0)) * 2.0 / 3.0
    return ret

def transformLon(x, y):
    ret = 300.0 + x + 2.0 * y + 0.1 * x * x + 0.1 * x * y + 0.1 * math.sqrt(abs(x))
    ret += (20.0 * math.sin(6.0 * x * math.pi) + 20.0 * math.sin(2.0 * x * math.pi)) * 2.0 / 3.0
    ret += (20.0 * math.sin(x * math.pi) + 40.0 * math.sin(x / 3.0 * math.pi)) * 2.0 / 3.0
    ret += (150.0 * math.sin(x / 12.0 * math.pi) + 300.0 * math.sin(x / 30.0 * math.pi)) * 2.0 / 3.0
    return ret

以上代码段实现了从WGS84坐标系统到GCJ02坐标系统的转换。这是开发中一个实际的应用实例，展示了编程在解决特定地理信息问题上的灵活性和强大功能。

以上内容涵盖了从使用现有的坐标转换工具到掌握手动计算公式的技巧，再到通过编程实现自动化转换的实用技巧。无论是在地理信息系统分析、导航定位系统开发，还是进行大数据空间分析中，这些技能都有着广泛的应用价值。

# 4. 经纬度转换的高级应用

## 4.1 坐标转换在地图制作中的应用

### 4.1.1 地图投影的选择和应用

地图制作是地理信息系统（GIS）中的一项重要应用，而地图投影是实现三维地球表面到二维平面的转换技术。正确的选择和应用地图投影对地图的精确度和使用效果至关重要。地图投影通常分为三大类：圆柱投影、圆锥投影和方位投影。

在圆柱投影中，地球表面被投影到一个与之接触的圆柱面上，然后展开到平面。如墨卡托投影是一种等角圆柱投影，广泛应用于航海和航空地图。它的特点是保持了地图上所有方向的角度，但会造成极地区域的面积变形。

圆锥投影则将地球表面投影到一个锥面上，再展开到平面。这种投影能够较好地保持面积比例，适用于中纬度区域的地图制作，例如兰伯特等角圆锥投影。它通过调整圆锥与地球接触的方式，使得在特定纬度上的角度和面积变形最小化。

方位投影，或称为心射投影，将地球表面投影到通过地心的平面上。这种投影类型多用于展示地球的极地地区。例如，极射赤面投影将地球的北极或南极投影到一个平面，展现出极地附近的区域。

选择合适投影的一个关键步骤是评估地图的具体用途。例如，对于全球范围的导航，墨卡托投影可能是最佳选择；而对于特定国家的详细地图制作，可能需要选择一个国家范围内的投影标准。

在地图制作过程中，坐标转换通常涉及到从一个地理坐标系统（GCS）到一个投影坐标系统（PCS）的转换。转换过程中必须考虑地图的尺度、用途和用户的需求，确保地图的精度和可用性。例如，一个城市规划地图可能需要使用国家地图局制定的正射投影，以确保面积和形状的准确性。

### 4.1.2 多源数据整合时的坐标转换

在地理信息系统（GIS）中，经常需要将来自不同源的数据整合到一个统一的参考框架下。这些数据可能包括卫星图像、不同比例尺的地图、地表高程数据等。为了确保这些数据能够在同一幅地图上正确叠加，必须执行精确的坐标转换。

多源数据整合过程中的坐标转换包括几个关键步骤：

1. **数据定位**：首先确定每个数据源的坐标系统，了解它们是地理坐标系统（GCS）还是投影坐标系统（PCS）。

2. **转换到统一坐标系统**：根据数据集的具体情况，将所有数据转换到一个共同的坐标系统中。如果原始数据使用的是不同的地理坐标系统（如WGS84和CGCS2000），需要先进行GCS之间的转换。

3. **投影转换**：如果数据是投影坐标系统，则需要确保它们使用的是相同的投影参数。对于非统一投影的数据，执行PCS之间的转换。

4. **尺度调整**：不同数据源可能有不同的尺度和分辨率。为了整合，需要对数据进行重新采样和尺度调整，以匹配目标坐标系统。

5. **误差校正**：在转换和整合过程中，不可避免地会产生一些误差，包括系统误差和随机误差。需要进行误差分析，并进行必要的校正以提高数据一致性。

6. **数据验证**：最后，需要验证转换后的数据与原始数据的一致性。这通常涉及在特定检查点上比较坐标值，并评估整体数据集的准确度。

在实际操作中，可以使用GIS软件（如ArcGIS或QGIS）来自动化以上步骤。例如，在ArcGIS中，可以通过空间参考系统管理器来定义和转换坐标系统。此外，还可以编程实现这些功能，使用如GDAL/OGR库中的工具和函数来执行坐标转换和数据处理。

## 4.2 移动端地理位置服务

### 4.2.1 GPS定位原理与经纬度获取

全球定位系统（GPS）已经成为大多数现代智能手机的标准功能，为各种基于位置的服务（LBS）提供支持。GPS通过计算用户设备与地球轨道上卫星的距离来确定用户的地理位置，从而提供经纬度坐标。

GPS定位的基本原理是基于卫星和接收器之间的测距。接收器（用户设备）测量来自至少四个不同卫星的无线电信号的传输时间。由于无线电信号以光速传播，通过测量传输时间可以精确计算出卫星到接收器的距离。当接收器接收到来自多颗卫星的信号并计算出距离时，就可以在一个三维空间内确定接收器的位置。

使用GPS获得的经纬度坐标是地理坐标系统（GCS）中的点，以度（°）为单位。经度表示东（正值）或西（负值）与格林威治子午线的角度差，而纬度表示从赤道（0°）向北（正值）或向南（负值）的角度差。

现代智能手机通常使用辅助GPS技术（A-GPS）来加快定位速度并提高定位精度。A-GPS利用移动网络或其他无线技术，将GPS卫星轨道数据、时间数据和位置信息传输到设备，使设备能够快速锁定卫星信号。

为了支持更多的位置服务，智能手机操作系统如Android和iOS提供了内置的地理位置服务API。开发者可以通过这些API来获取用户的位置信息，然后执行坐标转换操作以适配特定的地理信息系统或地图服务。

### 4.2.2 移动端应用中的坐标转换技术

由于移动设备的广泛普及，许多企业和开发者都希望在他们的应用中集成位置相关功能。然而，由于用户可能在全球任何位置使用应用，这就要求应用能够处理各种不同的地理位置数据格式和坐标系统。

在移动应用中实现坐标转换的技术包括：

1. **内置API使用**：如Android的LocationManager和iOS的Core Location框架，它们可以帮助开发者获取设备的当前位置，并将这些坐标转换为常用的格式，如WGS84。

2. **第三方库应用**：有些第三方库如Proj4J和Leaflet Proj4Plugin提供了丰富的坐标转换功能，可以方便地在移动应用中集成复杂的坐标转换。

3. **自定义转换逻辑**：在某些情况下，开发者可能需要实现自定义的坐标转换逻辑。例如，将设备获取的GPS坐标转换为特定国家的国家地图投影。

4. **云服务利用**：云服务提供商如Google Cloud和Amazon Web Services，可以为开发者提供计算密集型的坐标转换服务，从而减少移动设备的计算负担。

5. **实时更新和调整**：移动设备的GPS可能会受到建筑物遮挡或城市峡谷效应的影响，应用需要实现实时的坐标更新和调整机制，以保持位置数据的准确性。

6. **位置数据的安全性和隐私**：在移动应用中处理地理位置数据时，必须考虑用户隐私和数据安全。开发者需要遵守相关法律法规，如欧盟的GDPR或加州的CCPA，确保用户的位置信息得到妥善保护。

## 4.3 大数据中的空间坐标分析

### 4.3.1 处理海量地理信息数据的技术

随着物联网（IoT）和移动设备的广泛使用，海量的地理信息数据正在被收集和存储。这些数据包括但不限于GPS追踪数据、社交网络签到信息、交通流量监测数据等。为了从这些海量数据中提取有价值的信息，需要使用高级的数据处理技术和算法。

处理这些空间大数据的关键技术包括：

1. **分布式计算框架**：使用如Apache Hadoop或Apache Spark这样的分布式计算框架，可以在大规模数据集上运行复杂的坐标转换和空间分析算法。这些框架可以支持水平扩展，处理PB级别的数据。

2. **空间数据库**：空间数据库如PostGIS是PostgreSQL的扩展，提供存储和管理空间数据的能力，可以执行各种空间查询和分析。空间数据库支持空间索引，可以快速检索空间信息。

3. **空间分析工具**：使用空间分析工具，如QGIS、GRASS GIS，可以对大量地理数据进行可视化和分析。这些工具支持从基础的空间查询到复杂的地理建模。

4. **机器学习算法**：机器学习算法，特别是地理空间机器学习算法，能够从空间数据中识别模式和趋势。深度学习模型，如卷积神经网络（CNNs）和循环神经网络（RNNs），已经被应用于地理空间数据分析。

5. **空间数据流处理**：空间数据流处理系统，如Apache Storm和Apache Flink，可以实现实时或近实时的空间数据分析，对于位置服务和监控系统尤其重要。

6. **云计算服务**：云服务提供商如Google Cloud Platform和Amazon Web Services，提供了强大的空间分析工具和服务。这些工具和服务可以处理和分析大量的地理空间数据，并提供易于使用的API接口。

### 4.3.2 坐标转换在空间数据分析中的角色

在空间数据分析中，坐标转换通常发生在数据整合和查询阶段，它有助于将空间数据从一个坐标系统转换到用户或分析工具可操作的格式。具体来说，坐标转换在空间数据分析中的角色包括：

1. **数据集成**：由于不同的地理信息系统可能使用不同的坐标系统，坐标转换成为将多源数据整合到一个共同的参考框架下的关键步骤。

2. **查询和比较**：为了对不同来源的空间数据进行查询和比较，需要确保这些数据都在同一个坐标系统中。

3. **可视化**：将数据坐标转换为视觉上可解释的形式是空间数据分析的一个重要部分。坐标转换可以保证数据在地图上的正确显示。

4. **分析和建模**：在执行空间分析和建模时，坐标转换是必要的步骤，以确保模型的精度和结果的正确性。

5. **决策支持**：空间数据分析的一个重要目标是支持决策过程。通过坐标转换，可以确保基于地理位置的决策支持系统中的数据准确无误。

6. **实时分析**：现代应用经常需要实时或近实时的数据分析，坐标转换技术使得从原始地理位置数据到分析结果的处理过程更加高效和准确。

在实施空间数据的坐标转换时，需要考虑转换后的数据在时间和空间上的一致性，以及数据的准确性和完整性。例如，在城市交通流量分析中，车辆GPS数据可能需要从WGS84转换到城市特定的投影系统，以确保流量数据的准确性和分析模型的有效性。

处理海量空间数据并执行坐标转换通常涉及到复杂的计算过程。因此，开发者和数据分析师需要了解如何使用相关的软件工具和编程库来简化这一过程。例如，Python的geopandas库提供了强大的地理空间数据处理功能，可以执行坐标转换，并进行空间分析。而GDAL/OGR库提供了一系列的命令行工具和编程接口，用于处理、转换和分析空间数据。

## 代码块示例：使用Python的geopandas和GDAL/OGR库进行坐标转换

import geopandas as gpd
from osgeo import ogr, osr

# 创建源坐标系对象
src_crs = osr.SpatialReference()
src_crs.ImportFromEPSG(4326)  # WGS84坐标系统

# 创建目标坐标系对象
dst_crs = osr.SpatialReference()
dst_crs.ImportFromEPSG(3857)  # Web Mercator投影

# 创建坐标转换对象
transform = osr.CoordinateTransformation(src_crs, dst_crs)

def transform_coordinates(x, y, transform):
    # 创建点对象
    point = ogr.Geometry(ogr.wkbPoint)
    point.AddPoint(x, y)
    # 进行坐标转换
    point.Transform(transform)
    return point.GetX(), point.GetY()

# 示例坐标点转换
original_point = transform_coordinates(-73.985656, 40.748433, transform)
print(f"转换后的坐标: ({original_point[0]}, {original_point[1]})")

在上面的代码示例中，首先导入了geopandas库和GDAL/OGR库的osr模块。然后，创建了WGS84和Web Mercator投影的坐标系统对象。接着，定义了一个坐标转换对象。最后，创建了一个转换坐标的函数，并演示了如何将一个GPS坐标点从WGS84转换为Web Mercator投影。

代码中的`transform_coordinates`函数接收原始经纬度坐标，并使用定义好的坐标转换对象进行转换。返回的转换坐标是以Web Mercator投影表示的。

这个过程展示了如何使用编程来处理复杂的坐标转换任务，并为地理空间数据分析提供支持。此外，开发者可以使用此方法将任何地理空间数据转换到所需的坐标系统中。

# 5. 经纬度转换案例分析

## 5.1 航海导航系统中的应用案例

### 5.1.1 航海导航中的坐标转换需求

在航海导航中，坐标转换是确保船舶准确航行的核心技术之一。由于地球是一个近似的椭球体，而非完美的球体，因此航海中采用的坐标系统必须能够准确描述地球的曲率。在这一过程中，从WGS84坐标系（全球定位系统使用的坐标系）转换到航海使用的网格坐标系（如UTM）是一个关键步骤。这些转换必须在保证极高精度的同时，快速高效地进行，因为任何的计算延误或误差都可能导致海上安全风险。

### 5.1.2 实际应用中的转换精度和方法

在实际操作中，使用了多种技术手段确保转换的准确性。首先，通过高精度的GPS设备，实时获取船舶的WGS84坐标。然后，利用预先定义好的转换参数将这些坐标转换到UTM坐标系中。在转换过程中，除了线性转换外，还需要考虑地球曲率和投影变形，这就需要采用复杂的数学模型和算法。现代船舶导航系统通常使用高精度的算法和预先计算好的查找表来实现快速且精确的转换。这种转换不仅需要考虑到地球的形状和海图投影的特性，还需要考虑到地磁变化、潮汐等因素，因此，导航系统中集成的坐标转换模块必须具备高度的灵活性和可扩展性。

## 5.2 GIS项目中的坐标转换案例

### 5.2.1 GIS项目中常见的转换问题

地理信息系统（GIS）项目通常会遇到多种坐标系统的转换问题，尤其是在处理跨地区或国家的数据时。比如，一个项目可能需要结合使用来自不同国家的地理数据，而这些数据可能使用了不同的地理坐标系统或投影坐标系统。这种情况下，如果不进行正确的坐标转换，数据将会出现位置偏差，这将直接影响GIS项目的分析结果和决策质量。

### 5.2.2 解决方案和最佳实践

为了解决GIS项目中的坐标转换问题，最佳实践包括使用专业GIS软件中内置的坐标转换工具，例如ArcGIS或QGIS。这些工具通常会内置多种坐标系统，并提供了强大的转换算法。在进行转换时，应首先确认需要转换到的目标坐标系统，然后使用软件提供的转换功能，输入源数据的坐标系统参数，并进行转换。如果标准工具无法满足特定需求，还可以通过编写自定义脚本（例如使用Python脚本与GDAL库）进行精确控制。在GIS项目中，常常还需要利用元数据和转换日志记录来跟踪转换过程中的参数设置和任何可能发生的错误，确保转换结果的可追溯性和数据的完整性。

### 代码示例与解析

以下是一个使用Python和GDAL库进行坐标转换的简单示例代码：

from osgeo import osr

# 创建源坐标系统和目标坐标系统的对象
src = osr.SpatialReference()
tgt = osr.SpatialReference()

# 加载WGS84坐标系统
src.ImportFromEPSG(4326)
# 加载UTM投影坐标系统
tgt.ImportFromEPSG(32633)

# 创建坐标转换对象
transform = osr.CoordinateTransformation(src, tgt)

# 输入源坐标点（经度，纬度）
point = transform.TransformPoint(116.39128, 39.90704)
# 输出转换后的坐标点
print(point)

### 参数说明

- `4326`: WGS84坐标系统的EPSG代码。
- `32633`: 中国区域的UTM投影坐标系统的EPSG代码。
- `TransformPoint`: 执行坐标转换操作的方法，需要传入经度和纬度值。

### 逻辑分析

这段代码首先导入了GDAL库中的osr模块，该模块提供了处理坐标系统转换的功能。通过指定EPSG代码，我们加载了WGS84和UTM两个坐标系统。接着，创建了一个转换对象，并用它将一个给定的WGS84坐标点转换为UTM坐标点。这种方法适用于GIS项目中需要进行坐标系统转换的场景，可以大大提高数据处理的效率和准确性。

### 5.2.3 案例小结

以上所述案例分析展示了在特定应用中坐标转换的实际需求以及如何有效解决这些需求。无论是航海导航还是GIS项目，坐标转换都是一个必不可少的技术环节。确保转换过程的精确性不仅可以提升系统的可靠性，还可以为用户提供更为准确的地理信息。通过对案例的深入分析，可以更好地理解坐标转换的复杂性及其在解决实际问题中的应用。

# 6. 经纬度转换技巧进阶与展望

随着全球化以及数字化的发展，经纬度转换已经成为了地理信息科学、测绘学和相关IT领域中不可或缺的一部分。本章节将对经纬度转换技术的未来发展趋势进行展望，并探讨个人和组织如何学习和应用这些技巧。

## 6.1 未来坐标转换技术的发展趋势

### 6.1.1 新兴技术在坐标转换中的应用前景

新兴技术如人工智能、云计算和物联网的发展，正在改变我们处理地理信息数据的方式。在坐标转换领域，这些技术同样展现出巨大潜力。

- **人工智能（AI）**：AI和机器学习可以用来分析和优化转换过程中的算法。通过大数据训练，AI模型可以识别和校正转换中的复杂误差，并实现自动化转换，提高准确性和效率。

- **云计算**：通过云平台提供的高性能计算资源，可以实现海量地理数据的快速处理和转换。云服务还能提供可扩展的存储空间，方便数据的存储和备份。

- **物联网（IoT）**：IoT设备如传感器等，能够实时收集地理位置数据。这些数据需要通过精确的坐标转换，以便于在不同的应用和系统中使用。

### 6.1.2 跨平台坐标统一标准化的挑战与机遇

跨平台的坐标统一标准化是目前面临的一大挑战。不同系统和设备采用不同的坐标系统，如何实现这些系统间的数据无缝转换和共享，是当前亟需解决的问题。

- **标准化工作**：国际标准化组织正在努力推动坐标系统和转换方法的标准化进程。这为坐标转换技术的兼容性和互操作性提供了可能。

- **开放API和服务**：开放的API和在线转换服务可以作为统一的接口，简化跨平台的坐标转换流程。

## 6.2 个人和组织如何学习和应用

### 6.2.1 推荐的学习资源和方法

掌握坐标转换技术不仅需要理论知识，也需要实践操作。以下是一些推荐的学习资源和方法：

- **在线课程和教程**：目前，许多在线教育平台如Coursera、edX、Udemy等都提供了相关的在线课程，涵盖了从基础知识到高级应用的完整学习路径。

- **专业书籍和文献**：通过阅读专业书籍和最新的研究文献，可以更深入地理解坐标转换的原理和技术。

- **实践操作**：通过实际操作不同的坐标转换工具和编程实践，可以加深对理论的理解并获得宝贵的实践经验。

### 6.2.2 坐标转换技能在职业发展中的价值

掌握坐标转换技能对于个人职业发展具有重要意义：

- **测绘和地理信息系统专业**：对于测绘和GIS相关领域的专业人士，熟悉坐标转换是基本技能之一。

- **IT和数据分析**：在IT行业和数据分析工作中，处理地理位置数据时经常需要应用坐标转换技能，它有助于提高数据处理的准确性和应用的广度。

- **新兴行业**：随着无人驾驶、智慧城市、虚拟现实等新兴行业的发展，坐标转换技能将变得更加重要。

在学习和应用经纬度转换的过程中，个人和组织需要不断适应技术的发展，更新知识体系，并且持续实践以掌握这些核心技能。随着时间的推移，坐标转换技术将更为先进和普及，为更多的应用场景提供支持。