MATLAB三维曲面拟合与可视化：揭秘数据的几何之美

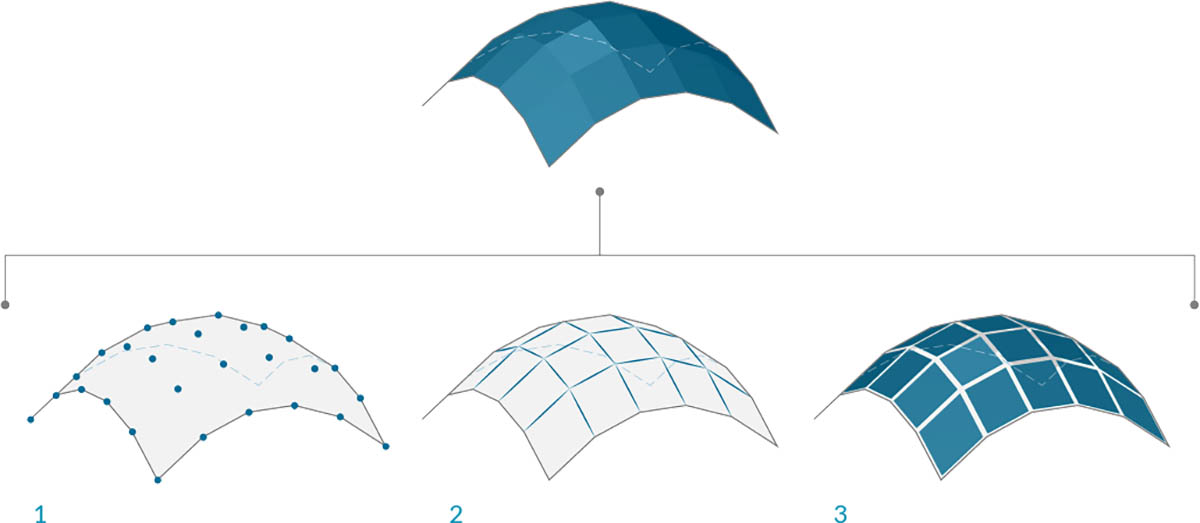
# 1. MATLAB三维曲面拟合基础**

三维曲面拟合是利用数学模型来逼近给定数据点集合所形成的曲面的过程。在MATLAB中，可以使用多种算法来进行三维曲面拟合，包括多项式拟合、插值法和最小二乘法。

多项式拟合通过使用多项式方程来逼近曲面，而插值法则通过生成通过所有数据点的平滑曲线来逼近曲面。最小二乘法通过最小化拟合模型和数据点之间的误差来逼近曲面。

# 2. 三维曲面拟合算法

三维曲面拟合算法旨在通过已知的三维数据点，构建一个数学模型来近似描述曲面的形状。根据不同的拟合原则和数学方法，三维曲面拟合算法主要分为多项式拟合、插值法和最小二乘法。

### 2.1 多项式拟合

多项式拟合是一种经典的曲面拟合方法，它通过构造一个多项式函数来近似拟合曲面。

#### 2.1.1 一元多项式拟合

对于一元多项式拟合，假设曲面可以用一个一元多项式函数表示：

f(x) = a0 + a1x + a2x^2 + ... + anx^n

其中，a0, a1, ..., an为多项式的系数。通过最小化拟合误差，可以求解出这些系数，从而得到一元多项式拟合函数。

#### 2.1.2 多元多项式拟合

对于多元多项式拟合，曲面可以用一个多元多项式函数表示：

f(x, y, z) = a0 + a1x + a2y + a3z + a4xy + a5xz + a6yz + ...

其中，a0, a1, ..., an为多项式的系数。多元多项式拟合的过程与一元多项式拟合类似，通过最小化拟合误差来求解系数。

### 2.2 插值法

插值法是一种通过已知数据点直接构造曲面的方法。

#### 2.2.1 线性插值

线性插值是一种最简单的插值方法，它假设曲面在两个已知数据点之间是线性的。对于三个已知数据点(x1, y1, z1)、(x2, y2, z2)和(x3, y3, z3)，线性插值函数为：

f(x, y, z) = (1 - t) * (1 - s) * z1 + (1 - t) * s * z2 + t * (1 - s) * z3 + t * s * z4

其中，t = (x - x1) / (x3 - x1)，s = (y - y1) / (y3 - y1)。

#### 2.2.2 样条插值

样条插值是一种分段插值方法，它假设曲面在每个数据点之间的区域内是多项式函数。样条插值函数由多个多项式函数拼接而成，每个多项式函数在自己的区域内拟合曲面。样条插值可以提供比线性插值更光滑的曲面。

### 2.3 最小二乘法

最小二乘法是一种通过最小化拟合误差来构造曲面的方法。

#### 2.3.1 线性最小二乘拟合

线性最小二乘拟合假设曲面可以用一个线性函数表示：

f(x, y, z) = a0 + a1x + a2y + a3z

通过最小化拟合误差，可以求解出系数a0, a1, a2和a3，从而得到线性最小二乘拟合函数。

#### 2.3.2 非线性最小二乘拟合

非线性最小二乘拟合假设曲面可以用一个非线性函数表示：

f(x, y, z) = a0 + a1exp(x) + a2sin(y) + a3cos(z)

求解非线性最小二乘拟合函数需要使用迭代算法，例如Levenberg-Marquardt算法。

# 3. MATLAB三维曲面拟合实践

### 3.1 数据预处理

#### 3.1.1 数据清理和转换

在进行三维曲面拟合之前，数据预处理是至关重要的。数据预处理包括以下步骤：

- **数据清理：**删除异常值、缺失值和噪声数据。异常值可以通过箱线图或 Grubbs 检验等方法识别。缺失值可以通过插值或删除来处理。噪声数据可以通过平滑或滤波技术来去除。
- **数据转换：**将数据转换为适合拟合模型的格式。例如，对于多项式拟合，数据需要转换为矩阵形式。对于插值法，数据需要转换为一组点。

#### 3.1.2 数据归一化和标准化

数据归一化和标准化可以提高拟合模型的精度和稳定性。

- **数据归一化：**将数据缩放到 [0, 1] 或 [-1, 1]