R语言数据结构深度解析：掌握向量、矩阵、数组与数据框的高级技巧

# 1. R语言数据结构的基本概念

## 1.1 数据结构的定义与重要性
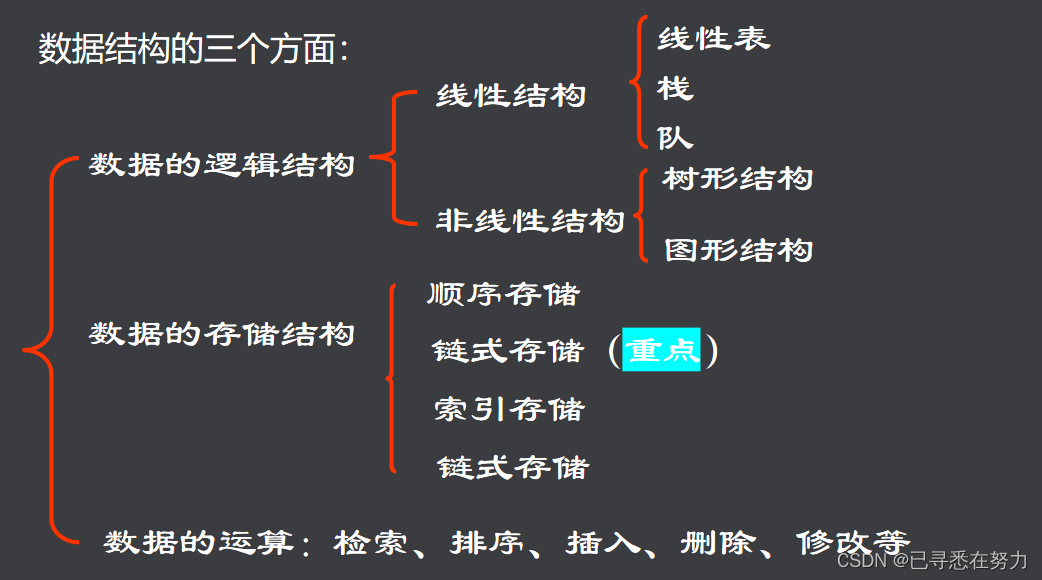
在数据分析和统计计算中，数据结构是基础。它们是组织和存储数据的方式，对数据的处理效率和复杂操作的实现有直接影响。R语言提供了丰富的数据结构，包括向量、矩阵、数组、数据框（data frame）等，这些结构各有特点，适用于不同类型的数据处理任务。

## 1.2 R语言数据结构的核心类型
- **向量(Vector)**：一维数组，包含相同类型的数据。
- **矩阵(Matrix)**：二维数组，所有的元素必须具有相同的数据类型。
- **数组(Array)**：可以看作是多维矩阵，数据类型同样需要一致。
- **数据框(Data Frame)**：类似于表格形式，可以包含不同类型的列，每列相当于一个变量。

## 1.3 数据结构的操作和应用
在本章中，我们将详细探讨每种数据结构的基本概念、创建方式、索引方法和常用操作。理解这些基础概念将为处理更复杂的数据分析任务打下坚实的基础。

# 2. 向量的操作与应用

### 2.1 向量基础

#### 2.1.1 向量的定义和创建

在R语言中，向量是最基本的数据结构，用于存储一系列的值。一个向量可以包含数字、字符、逻辑值（TRUE或FALSE）或其他数据类型，但通常它们的数据类型是相同的。创建向量最简单的方式是使用`c()`函数。向量也可以通过`scan()`函数从外部数据源中读取数据，或者使用`vector()`函数创建一个指定长度的向量。

# 使用c()函数创建向量
numeric_vector <- c(1, 2, 3, 4, 5)
character_vector <- c("apple", "banana", "cherry")

# 使用scan()函数读取外部数据
# 假设从文件mydata.txt中读取
# numeric_vector <- scan("mydata.txt", what=numeric())

# 使用vector()函数创建指定长度的向量
empty_numeric_vector <- vector("numeric", length=10)

向量的创建涉及将数据元素依次排列在内存中，R语言提供了向量化的操作，意味着对向量的操作通常会被应用到向量的每个元素上。

#### 2.1.2 向量的索引和子集选择

索引是获取向量中特定元素的方式。在R中，向量的索引是从1开始的。可以使用方括号`[]`加上索引来访问向量中的元素。

# 创建一个向量
my_vector <- c("red", "green", "blue", "yellow", "pink")

# 访问第一个元素
first_element <- my_vector[1]

# 访问第三个到第五个元素
subset_vector <- my_vector[3:5]

# 访问不连续的元素
non_consecutive_vector <- my_vector[c(1, 3, 5)]

除了用数值进行索引外，还可以使用逻辑向量来进行条件筛选，仅返回满足条件的元素。

# 仅返回向量中颜色为"red"或"blue"的元素
filter_vector <- my_vector[my_vector %in% c("red", "blue")]

逻辑索引是向量操作中非常强大的一种工具，它允许我们基于条件对数据进行筛选，类似于SQL中的WHERE子句。

### 2.2 向量的高级操作

#### 2.2.1 向量化的函数应用

向量化函数指的是R语言中那些可以同时作用于向量所有元素的函数。这些函数通常比循环遍历每个元素执行操作更高效。例如，`sqrt()`函数用于计算平方根，可以应用于包含数字的向量。

# 创建一个数字向量
numbers <- c(1, 4, 9, 16)

# 向量化函数应用：计算每个元素的平方根
sqrt_numbers <- sqrt(numbers)

# 输出结果
print(sqrt_numbers)

#### 2.2.2 向量的比较和逻辑运算

向量的比较是元素之间的比较，通常返回一个逻辑向量。例如，我们可以比较两个向量的元素，判断它们是否相等。

# 创建两个数字向量
vector1 <- c(1, 2, 3)
vector2 <- c(1, 4, 3)

# 比较两个向量的元素是否相等
equality_result <- vector1 == vector2

# 输出比较结果
print(equality_result)

除了相等性比较外，还可以使用逻辑运算符如`<`, `>`, `<=`, `>=`, `!=`等对向量进行逻辑运算。

#### 2.2.3 向量缺失值处理技巧

向量中可能包含缺失值，通常用`NA`表示。处理缺失值是数据清洗中常见的任务。R语言提供了几种处理缺失值的函数。

# 创建包含缺失值的向量
vector_with_na <- c(1, NA, 3, 4, NA)

# 检查缺失值
na_check <- is.na(vector_with_na)

# 排除缺失值进行操作
filtered_vector <- na.omit(vector_with_na)

# 替换缺失值
replaced_vector <- replace(vector_with_na, is.na(vector_with_na), 0)

在实际操作中，我们可能需要根据具体需求使用不同的缺失值处理方法。例如，当计算平均值时，可以使用`mean()`函数，它默认排除`NA`值。

# 计算向量的平均值，排除NA值
mean_value <- mean(vector_with_na, na.rm=TRUE)

# 输出结果
print(mean_value)

### 表格和mermaid流程图

表格和流程图是帮助读者理解复杂概念的有效工具。下面是一个展示向量操作及其应用的流程图：

graph TD
    A[开始] --> B[创建向量]
    B --> C[向量索引]
    C --> D[向量逻辑索引]
    D --> E[向量化函数应用]
    E --> F[比较与逻辑运算]
    F --> G[处理缺失值]
    G --> H[结束]

| 操作类型 | 描述 |
|--------|------|
| 创建向量 | 使用`c()`、`scan()`或`vector()`函数创建向量 |
| 向量索引 | 使用方括号`[]`访问特定元素 |
| 向量逻辑索引 | 使用逻辑向量筛选满足条件的元素 |
| 向量化函数应用 | 应用函数到向量每个元素上 |
| 比较与逻辑运算 | 对向量元素进行比较和逻辑操作 |
| 处理缺失值 | 检查、排除或替换向量中的缺失值 |

### 代码块和参数说明

# 示例：使用向量化函数计算平方
numbers <- c(1, 2, 3, 4)
squared_numbers <- numbers^2
print(squared_numbers)

# 示例：逻辑索引的应用
color_vector <- c("red", "green", "blue", "yellow")
red_or_blue <- color_vector[color_vector %in% c("red", "blue")]
print(red_or_blue)

在上述代码中，`squared_numbers`向量是通过向量化操作`^2`直接计算出的，而`red_or_blue`向量则是通过逻辑索引方式筛选出的满足条件的颜色。对于`print()`函数，它用于输出R对象的内容，是进行调试和展示结果时常用的一种方式。

在本章中，我们详细探讨了向量的基础知识和高级操作，包括创建向量、使用索引访问元素、向量化函数的应用、比较与逻辑运算以及缺失值处理。通过这些基础和高级技能的学习，可以帮助用户更高效地处理和分析数据集。下一章我们将进一步深入，介绍矩阵和数组的操作技巧。

# 3. 矩阵和数组的操控技巧

## 3.1 矩阵的基本操作

### 3.1.1 矩阵的创建与维度控制

在R语言中，矩阵（matrix）是一种将数据按行和列排列的二维数组结构。创建矩阵的基本函数为`matrix()`。理解矩阵维度对于数据科学与统计分析至关重要，因为维度控制能够帮助我们进行正确的数据操作。

# 创建一个矩阵的示例
my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
print(my_matrix)

在上述代码中，`1:12` 表示从1到12的序列。`nrow = 3` 和 `ncol = 4` 分别指定了矩阵应该有3行4列。R默认是按列填充矩阵的，可以通过设置参数`byrow = TRUE`来改变填充方式。

理解矩阵的维度是进行复杂数据分析的基础，比如说，在进行线性代数运算时，矩阵维度不匹配将导致错误。因此，控制矩阵维度，确保数据能正确地被操作，是每位数据科学者的基本技能。

### 3.1.2 矩阵的运算和行列操作

矩阵运算包括加法、减法、乘法等，此外还有行列式（determinant）的计算，特征值（eigenvalues）和特征向量（eigenvectors）的提取等。这些运算在数学建模与数据分析中十分常见。

# 矩阵加法示例
matrix_a <- matrix(1:4, nrow = 2)
matrix_b <- matrix(5:8, nrow = 2)
sum_matrix <- matrix_a + matrix_b
print(sum_matrix)

# 计算行列式
det_matrix <- det(my_matrix)
print(det_matrix)

# 提取特征值和特征向量
eigen_matrix <- eigen(my_matrix)
print(eigen_matrix$values)
print(eigen_matrix$vectors)

矩阵运算的每个步骤都是数据分析与机器学习中的重要组成部分。在实际应用中，矩阵的行列操作通常与数据处理紧密相关。比如在处理时间序列数据时，转置矩阵经常用于调整数据的结构以满足分析模型的需求。掌握矩阵的运算和行列操作，可以大幅提高数据处理的效率和准确性。