MATLAB非线性振动模态分析：深入问题解决之道

目录
摘要
关键字
1. MATLAB在振动模态分析中的作用

1.1 MATLAB在振动模态分析中的优势
1.2 振动模态分析的基本概念

2. 非线性振动模态分析的理论基础

2.1 非线性振动的基本概念

2.1.1 线性振动与非线性振动的区别
2.1.2 非线性振动系统的特点和分类

2.2 非线性振动方程的建立

2.2.1 动力学系统方程的推导
2.2.2 模态分析的基本方程

2.3 非线性振动模态的理论解法

2.3.1 解析方法概述
2.3.2 数值方法的应用

3. MATLAB在非线性振动模态分析中的实践应用

3.1 MATLAB仿真环境的搭建

3.1.1 MATLAB软件的安装和配置

解锁专栏，查看完整目录
摘要
本文探讨了MATLAB在振动模态分析中的应用及其在非线性振动系统分析中的作用。首先介绍了非线性振动模态分析的理论基础，包括基本概念、振动方程的建立和理论解法。随后，文章重点讨论了MATLAB在非线性振动模态分析中的实践应用，包括仿真环境的搭建、振动模态仿真及结果分析与可视化。进一步地，文章探讨了非线性振动模态分析的高级技术，例如参数激励、多尺度分析、混沌分析和振动控制策略。最后，通过一个工程案例研究，展示了MATLAB在工程振动模态分析中的实际应用，并对未来发展进行了展望。
关键字
MATLAB；振动模态分析；非线性振动；理论基础；仿真环境；参数激励；多尺度分析；混沌分析；振动控制；案例研究
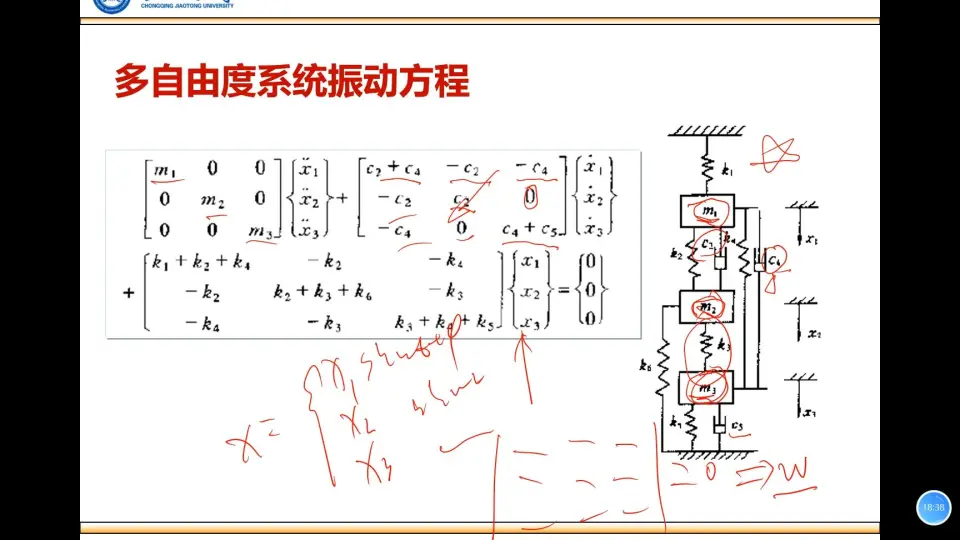
参考资源链接：MATLAB在振动模态分析中的应用与多自由度建模
1. MATLAB在振动模态分析中的作用
在工程领域，振动模态分析是理解结构动态响应的关键技术。MATLAB（Matrix Laboratory的缩写）作为一种高性能的数值计算和可视化软件，在振动模态分析中扮演了至关重要的角色。它不仅提供了强大的数值计算能力，还集成了丰富的工具箱，使得工程师能够在同一个平台上完成从理论建模到数据分析的全过程。
1.1 MATLAB在振动模态分析中的优势
MATLAB之所以在振动模态分析中备受青睐，主要得益于其以下几个优势：

强大的数学运算能力：MATLAB提供了丰富的数学函数库，可以高效地处理矩阵运算、线性代数、微积分等复杂计算。
专业的工具箱支持：如Simulink和Signal Processing Toolbox等，支持系统建模、仿真和信号处理，这些工具箱极大地扩展了MATLAB在振动模态分析上的应用。
直观的图形用户界面：MATLAB可以生成各种二维和三维的图形，方便工程师直观地展示和分析模态结果。

1.2 振动模态分析的基本概念
振动模态分析主要研究的是系统振动的固有特性，包括模态频率、振型和阻尼等参数。通过这些参数，可以预测系统的动态行为，并为结构设计和振动控制提供理论依据。
在后续章节中，我们将深入探讨非线性振动模态分析的理论基础，并结合MATLAB的实践应用，进一步阐释如何在工程实践中运用这些知识解决具体问题。
2. 非线性振动模态分析的理论基础
2.1 非线性振动的基本概念
2.1.1 线性振动与非线性振动的区别
在研究振动问题时，线性振动和非线性振动是两种不同的力学模型。线性振动系统的特征是符合叠加原理，即系统的响应是激励的线性函数。然而，大多数实际的物理系统都表现出非线性特性，其响应不再是激励的简单线性函数。非线性振动系统的特点是具有复杂的动态行为，可能表现出频率锁定、跳跃现象、混沌运动等非线性特征。
举个简单的例子，单摆就是一个典型的非线性振动系统，其运动方程在小角度时近似为线性，而在大角度摆动时就成为非线性。相较于线性振动系统，非线性振动系统难以用解析方法求解，因此数值方法变得至关重要。
2.1.2 非线性振动系统的特点和分类
非线性振动系统具有以下特点：

多解性：同一个系统在同样的初始条件下可能有不同的响应。
分叉现象：系统参数变化可能导致系统行为发生质的变化。
混沌现象：在某些条件下，系统的运动看似随机且无周期性。
频率耦合：系统可能同时具有多个频率成分。

非线性振动系统可以根据系统的性质和特点进行分类，主要分为以下几类：

自激振动系统：系统不需要外部激励，其内部能量转换机制可以维持振动。
参数振动系统：系统的某些参数随时间变化，导致系统振动特性改变。
强迫振动系统：系统受到外部周期性激励的影响。
内共振系统：系统中两个或多个自由度的频率比接近整数比，导致能量在各自由度之间转移。

2.2 非线性振动方程的建立
2.2.1 动力学系统方程的推导
动力学系统方程通常由牛顿第二定律得到，即系统的动力学行为由质量、阻尼和刚度（或弹簧常数）等参数决定。对于复杂系统，我们通常需要应用拉格朗日或哈密顿原理来推导出系统的运动方程。非线性系统的方程一般形式为：
[ \mathbf{M}(\mathbf{x})\ddot{\mathbf{x}} + \mathbf{C}(\mathbf{x}, \dot{\mathbf{x}})\dot{\mathbf{x}} + \mathbf{K}(\mathbf{x})\mathbf{x} = \mathbf{F}(\mathbf{x}, \dot{\mathbf{x}}, \ddot{\mathbf{x}}, t) ]
这里，(\mathbf{M})、(\mathbf{C}) 和 (\mathbf{K}) 分别代表质量矩阵、阻尼矩阵和刚度矩阵；(\mathbf{x})、(\dot{\mathbf{x}})、(\ddot{\mathbf{x}}) 分别表示位移、速度和加速度向量；(\mathbf{F}) 是外力向量。
2.2.2 模态分析的基本方程
模态分析用于研究系统的固有振动特性，即在无外部激励的情况下，系统的自由振动。其基本方程是特征值问题，可以表示为：
[ \mathbf{K}\boldsymbol{\Phi} = \omega^2 \mathbf{M}\boldsymbol{\Phi} ]
其中，(\boldsymbol{\Phi}) 是模态形状矩阵，而 (\omega) 是系统的自然频率。该方程求解的是系统无阻尼自由振动时的特征值和特征向量。
2.3 非线性振动模态的理论解法
2.3.1 解析方法概述
解析方法主要利用数学变换和近似方法来求解非线性方程。例如，谐波平衡法、多尺度法、Krylov-Bogoliubov 方法等。这些方法可以提供对系统行为的深刻理解，但是它们都有局限性，通常只适用于特定类型的非线性系统。
以谐波平衡法为例，这种方法假设系统的响应是由有限个谐波组成的，然后通过平衡激励和响应中的谐波来求解系统的稳态响应。这要求事先知道系统的某些特性，比如主要的频率成分。
2.3.2 数值方法的应用
对于无法解析求解的复杂非线性系统，数值方法成为研究非线性振动模态的重要工具。数值方法如有限元法(FEM)、时间步进法、Runge-Kutta方法等，可以模拟系统的动态行为并求解非线性微分方程。数值模拟不仅可以获得系统的稳态响应，还可以研究系统的瞬态响应和动力学行为。
下面是一个利用MATLAB进行数值求解的代码示例：
% 定义非线性振动系统方程f = @(t, y) [-y(2); -sin(y(1)) + y(2)^3];% 初始条件y0 = [1; 0];% 时间跨度tspan = [0 20];% 使用ode45求解器进行数值求解[t, y] = ode45(f, tspan, y0);% 绘制结果plot(t, y(:,1))xlabel('Time')ylabel('Displacement')title('Displacement vs Time')
该代码定义了一个非线性振动方程，并使用ode45求解器来数值求解该方程。求解器基于Runge-Kutta方法计算了振动的位移随时间的变化，并将结果绘制成图表。通过调整初始条件、时间跨度和求解器参数，可以模拟不同的振动行为和系统动态特性。
通过以上理论与实例相结合的分析，我们已经对非线性振动模态分析有了初步的了解。接下来，我们将在实际应用中进一步深入探讨如何利用MATLAB进行仿真与分析。
3. MATLAB在非线性振动模态分析中的实践应用
3.1 MATLAB仿真环境的搭建
在本章节中，我们将详细介绍如何搭建MATLAB仿真环境，这对于进行非线性振动模态分析来说是一个关键步骤。我们将从MATLAB软件的安装和配置开始，然后介绍相关工具箱的使用。
3.1.1 MATLAB软件的安装和配置
MATLAB，即矩阵实验室，是由MathWorks公司开发的一款高性能数值计算和可视化软件。安装MATLAB之前，需要确保你的计算机满足MATLAB的