强化学习中的时间差学习：理论与实践的完美结合（完整教程）

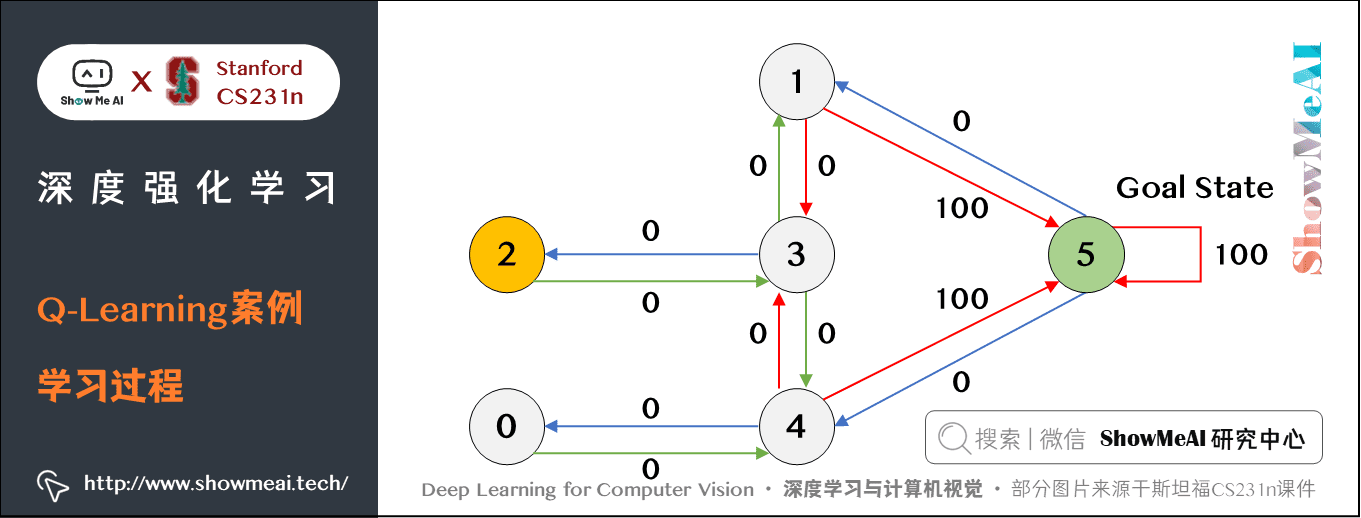
# 1. 时间差学习简介**

时间差学习是一种强化学习技术，它通过估计未来奖励的价值来指导当前决策。与传统监督学习不同，时间差学习不需要明确的标签，而是通过试错来学习最佳行动策略。

时间差学习的关键思想是，当前决策的价值不仅取决于立即奖励，还取决于未来潜在的奖励。通过考虑未来奖励，时间差学习算法可以做出更明智的决策，从而最大化长期回报。

# 2. 时间差学习理论基础

### 2.1 时间差学习的数学原理

时间差学习是一种基于马尔可夫决策过程（MDP）的强化学习方法。MDP是一个五元组(S, A, P, R, γ)，其中：

- S是状态空间，包含所有可能的状态。
- A是动作空间，包含所有可能采取的动作。
- P是状态转移概率函数，定义了从状态s采取动作a后进入状态s'的概率。
- R是奖励函数，定义了采取动作a后获得的奖励。
- γ是折扣因子，用于权衡未来奖励的价值。

时间差学习的目标是找到一个策略π，该策略可以最大化从初始状态开始的期望累积奖励。策略π定义了在每个状态下采取的最佳动作。

### 2.2 贝尔曼方程和价值函数

贝尔曼方程是时间差学习的理论基础。它描述了在给定策略π下，从状态s开始的期望累积奖励：

V_π(s) = E_π[R_t + γV_π(S_{t+1}) | S_t = s]

其中：

- V_π(s)是状态s的价值函数，表示从s开始并遵循策略π的期望累积奖励。
- R_t是时间步t获得的奖励。
- S_{t+1}是时间步t+1的状态。

价值函数可以用来评估策略π的优劣。一个好的策略将具有较高的价值函数。

### 2.3 时间差学习算法

时间差学习算法通过迭代更新价值函数来学习最佳策略。最常用的时间差学习算法包括：

- **Q学习算法：**Q学习算法更新每个状态-动作对的Q值，表示从该状态采取该动作的期望累积奖励。
- **SARSA算法：**SARSA算法与Q学习算法类似，但它使用当前状态和动作来更新Q值，而不是当前状态和所有可能的动作。

#### 代码块：Q学习算法

def q_learning(env, episodes, learning_rate, discount_factor):
    """
    Q学习算法

    参数：
        env: 强化学习环境
        episodes: 训练回合数
        learning_rate: 学习率
        discount_factor: 折扣因子
    """

    # 初始化Q表
    q_table = np.zeros((env.observation_space.n, env.action_space.n))

    for episode in range(episodes):
        # 重置环境
        state = env.reset()

        # 循环直到终止状态
        while True:
            # 根据Q表选择动作
            action = np.argmax(q_table[state, :])

            # 执行动作并获取奖励和下一状态
            next_state, reward, done, _ = env.step(action)

            # 更新Q表
            q_table[state, action] += learning_rate * (reward + discount_factor * np.max(q_table[next_state, :]) - q_table[state, action])

            # 更新状态
            state = next_state

            # 如果终止状态，则退出循环
            if done:
                break

    return q_table

#### 代码逻辑分析：

- `q_learning`函数接受环境、训练回合数、学习率和折扣因子作为参数。
- 它初始化一个Q表，其中每个元素表示状态-动作对的Q值。
- 对于每个训练回合，它从环境的初始状态开始。
- 在每个时间步，它根据当前Q表选择动作。
- 它执行动作并获取奖励和下一状态。
- 它使用Q学习更新公式更新Q表。
- 它更新状态并重复该过程