系统集成全流程揭秘：模糊函数算法从理论到实际部署


# 摘要
系统集成与模糊函数算法是处理不确定性和模糊信息的有效工具，对提升智能决策支持系统的性能至关重要。本文首先概述了系统集成与模糊函数算法的基本概念和理论基础，包括模糊逻辑、模糊集合以及模糊函数的数学模型。接着，详细阐述了模糊函数算法的设计流程、实现技术和优化方法，强调了算法在系统集成中的实际应用和案例分析。最后，探讨了当前算法面临的挑战和未来可能的发展趋势，特别是在人工智能领域的应用潜力。本文旨在为研究人员和实践者提供一个全面理解模糊函数算法的框架，并激发进一步的技术创新。

# 关键字
系统集成；模糊函数算法；模糊逻辑；模糊集合；算法优化；人工智能

参考资源链接：[互模糊函数在时延频移联合估计中的算法分析](https://wenku.csdn.net/doc/nib6kqkfa3?spm=1055.2635.3001.10343)
# 1. 系统集成与模糊函数算法概述

## 1.1 系统集成的基础认知
系统集成是指将多个系统、模块或组件通过特定方式连接和组合，以实现更复杂的功能或提升整体性能。在现代信息技术领域，系统集成通常是实现企业级解决方案的关键步骤，涉及从硬件到软件、从内部系统到外部服务的各种资源整合。

## 1.2 模糊函数算法的引入
模糊函数算法是处理不确定性信息的重要工具，它在系统集成中发挥作用，特别是在那些输入数据或目标结果不精确的情况下。这种算法基于模糊逻辑，它与传统的二进制逻辑不同，能够处理介于真与假之间的模糊概念。

## 1.3 系统集成中的模糊函数算法优势
在系统集成的背景下，模糊函数算法能够提供更加灵活和适应性强的解决方案。由于其处理不确定性的能力，它在优化决策过程、改进数据分析方法和增强模式识别准确性等方面发挥重要作用。此外，随着集成系统日益复杂，模糊函数算法的引入可以减少对复杂系统结构的依赖，提升系统的鲁棒性。

# 2. 模糊函数算法的理论基础

### 2.1 模糊逻辑与集合论基础

#### 2.1.1 模糊集合的概念和性质

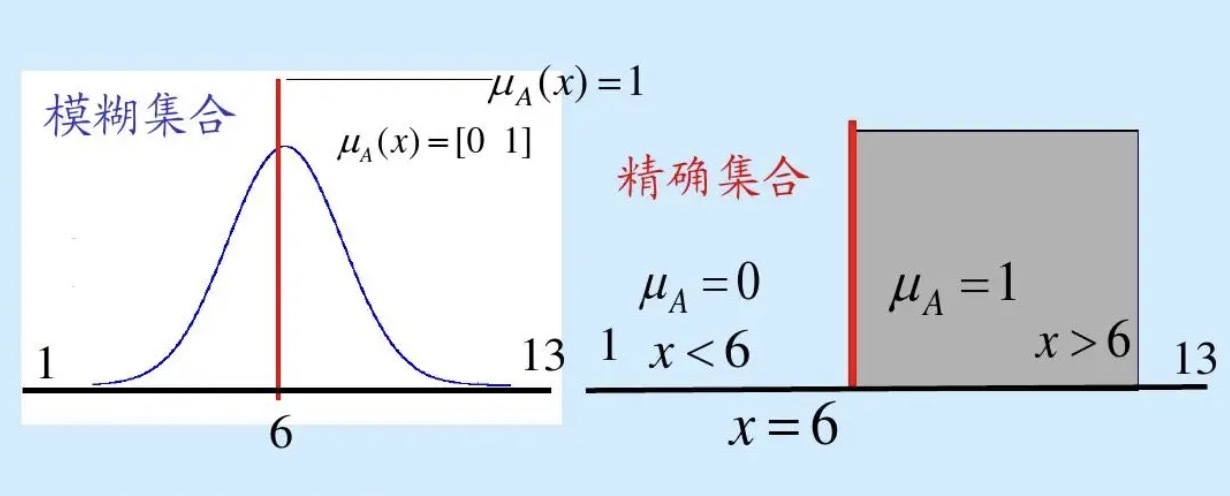
模糊集合理论是模糊函数算法的基石，与传统的二值逻辑不同，模糊集合允许元素对集合的隶属度在0和1之间取值。这种模糊性反映了现实世界中许多概念的非黑即白特性，例如“高”或“矮”、“热”或“冷”。

模糊集合的一个重要性质是其连续性，这允许对集合中的元素进行精细的划分。例如，在定义一个“温度”模糊集合时，可以有“冷”、“温和”、“热”等模糊集合并赋予相应的隶属度。

另一个性质是模糊集合的重叠性，它意味着同一元素可能同时属于多个模糊集合。例如，一个22摄氏度的温度，既可归属于“冷”集合也可归属于“温和”集合，不同的隶属度代表了它属于各集合的程度。

#### 2.1.2 模糊逻辑的基本原理

模糊逻辑是处理模糊概念和不确定性的推理逻辑。它由美国电气工程师L. A. Zadeh于1965年提出，并很快在控制理论、模式识别、决策分析等领域得到应用。

模糊逻辑的核心在于使用模糊变量来表示不确定性。这些变量是模糊集合上的元素，并且用隶属函数来表示其隶属度。模糊逻辑与经典逻辑的主要区别在于它能处理“部分真”或“部分假”的情况，而经典逻辑只关注“真”和“假”。

模糊逻辑的运算基于模糊集合和隶属度。例如，通过模糊逻辑可以定义“高温”和“湿气”两个模糊变量，并通过模糊规则进行推理，得出“不适感”的隶属度。这在控制空调系统时尤其有用，可以使得系统对室内温度和湿度的变化做出更自然的调节响应。

### 2.2 模糊函数算法的数学表达

#### 2.2.1 模糊函数的定义与类型

模糊函数是基于模糊集合理论，将输入的模糊变量映射到输出模糊变量的函数。它通过隶属函数来定义，隶属函数决定了输入变量对于某个特定模糊集合的隶属度。

模糊函数的类型很多，如模糊线性函数、模糊非线性函数等。模糊线性函数可以被用来表示简单的数学关系，而模糊非线性函数则能够处理更为复杂的系统行为。

#### 2.2.2 算法的数学模型和特性

模糊函数算法的数学模型通常基于模糊规则库和隶属函数来实现。模糊规则描述了输入变量之间的逻辑关系，并且指导算法如何根据隶属度进行决策。

在设计模糊函数算法时，需要考虑以下几个关键特性：

- 可扩展性：模糊函数算法能够适应不同数量和类型的输入输出变量。
- 鲁棒性：算法能够处理输入数据的不确定性和模糊性，给出稳定可靠的输出。
- 透明性：算法的决策过程应尽可能清晰，容易被理解和解释。
- 实时性：算法在处理数据时应保证低延迟，尤其是在对实时性要求高的应用场景中。

### 2.3 模糊函数算法的理论优势与局限性

#### 2.3.1 算法的优势分析

模糊函数算法的优势在于其处理模糊性和不确定性信息的能力。在许多现实世界的应用中，数据往往不是完全准确的，存在着大量的噪声和模糊性。例如，在人类语言理解和图像识别中，模糊函数算法可以提高系统对模糊指令或模糊图像的理解能力。

另一个显著优势是模糊函数算法能够模拟人类的决策过程。由于模糊逻辑与人类的自然语言和思维逻辑更为接近，算法可以更好地适应人的直觉和经验。

#### 2.3.2 算法的局限性及其适用场景

尽管模糊函数算法有诸多优势，但它也有局限性。首先，算法的性能在很大程度上依赖于模糊规则的设计。如果规则设计得不恰当，可能会导致输出结果与预期偏差较大。

其次，模糊函数算法在处理大规模数据集时可能会遇到计算效率和复杂性的问题。随着输入变量数量的增加，模糊规则的数量也会呈指数级增长，这会使得算法设计和优化变得更加困难。

此外，模糊函数算法在某些精确度要求极高的领域可能不是最佳选择。在这些场景中，更精确、可解释性强的算法可能更受青睐。

总的来说，模糊函数算法特别适用于那些需要模拟人类判断力，以及能够容忍一定程度模糊性的场景，例如专家系统、模糊控制等。

通过本章节的介绍，我们可以看出模糊函数算法的理论基础为后续章节中算法的设计、实现以及应用提供了坚实的基础。在下一章节中，我们将深入探讨模糊函数算法的设计与实现过程，及其在系统集成中的应用实践。

# 3. 模糊函数算法的设计与实现

模糊函数算法作为一种模拟人类推理能力的工具，在设计和实现过程中需要遵循特定的原则和步骤。在这一章节中，我们将详细介绍算法设计的关键步骤、技术要点以及优化与性能评估的方法。

## 3.1 算法设计的关键步骤

### 3.1.1 确定模糊变量和隶属函数

在模糊函数算法中，确定模糊变量和隶属函数是至关重要的第一步。模糊变量表示的是那些不确定的或者部分属于某一类的事物。而隶属函数则用来量化这个变量在不同模糊集中的隶属程度，它是一个在0到1之间取值的函数。

以一个简单的例子说明：

假设有一个温度控制系统，我们需要定义“冷”、“温和”、“热”这三个模糊变量，它们分别代表不同的温度范围。隶属函数可以采用三角形、梯形或者高斯形等不同的形状来表达，例如：

- 三角形隶属函数可以用三个参数（a, b, c）来定义，其中a和c是脚点，b是顶点。
- 梯形隶属函数由四个参数（a, b, c, d）定义，a和d为脚点，b和c为两个梯形的边。
- 高斯形隶属函数则通过均值（μ）和标准差（σ）来定义。

确定这些参数需要根据实际情况来设定，以确保隶属函数能够准确描述变量的模糊性。

### 3.1.2 设计模糊规则和决策逻辑

设计模糊规则和决策逻辑是模糊函数算法设计的第二步。模糊规则是通过“如果…那么…”的句式来表达的，它描述了输入变量和输出变量之间的模糊关系。一个典型的模糊规则可以表示为：“如果温度是冷而且湿度是干，那么舒适度是高”。

在设计模糊规则时，需要充分考虑输入变量之间的相互作用，以及它们对输出变量的影响力。决策逻辑则涉及如何根据模糊规则进行推理，以及如何将模糊结果转换为实际的决策或控制动作。

## 3.2 算法实现的技术要点

### 3.2.1 编程语言的选择与算法编程

在模糊函数算法的实现过程中，选择合适的编程语言是一个关键的技术要点。常见的编程语言包括但不限于C/C++、Python、Java和MATLAB等。每种语言都有其特定的优势，例如：

- C/C++具有较高的执行效率，适合资源受限的环境。
- Python具有丰富的库支持，适合快速原型开发。
- Java具有良好的跨平台特性，适合构建大型分布式系统。
- MATLAB则在