【数据结构实例分析】：清华题中的应用案例，你也能成为专家


# 摘要
本文全面探讨了数据结构在解决复杂问题中的应用，特别是线性结构、树结构、图结构、散列表和字符串的综合应用。文章首先介绍了数据结构的基础知识，然后分别探讨了线性结构、树结构和图结构在处理特定问题中的理论基础和实战案例。特别地，针对线性结构，文中详细阐述了数组和链表的原理及其在清华题中的应用；树结构的分析深入到二叉树及其变种；图结构则涵盖了图的基本理论、算法和高级应用案例。在散列表和字符串综合应用章节，文章讨论了散列表设计原理、冲突解决，以及字符串处理算法。最后，本文综合运用各种数据结构，进行算法效率分析和实战案例剖析，强调了数据结构选择和算法优化在解决问题中的重要性。通过本文的分析和案例，读者将能够更深刻理解数据结构在解决实际问题中的应用，并掌握如何优化算法效率。

# 关键字
数据结构；线性结构；树结构；图结构；散列表；算法效率

参考资源链接：[清华大学数据结构试题及答案](https://wenku.csdn.net/doc/6412b470be7fbd1778d3f99d?spm=1055.2635.3001.10343)
# 1. 数据结构的基础知识

数据结构是计算机存储、组织数据的方式，它决定了如何高效地访问和修改数据。对于任何一个计算机科学家或工程师来说，深入理解数据结构是基础中的基础。本章主要探讨了数据结构的核心概念，并为后续章节中涉及的具体结构和应用奠定基础。

## 1.1 数据结构的定义

数据结构是一组数据的组织、管理和存储格式，它使数据能够被高效地查询和修改。数据结构包括了数据元素的集合，以及在这些元素之间的关系和这些数据元素上的操作。数据结构通常与算法配合使用，以解决实际问题。

## 1.2 数据结构的重要性

为什么我们需要数据结构？在处理大量数据时，良好的数据结构能提高数据的处理速度和效率。举个例子，如果我们要管理大量的学生信息，一个合理的学生信息表将比简单地将所有信息存储在数组中更为高效。数据结构能够让我们更有效地访问、搜索、插入和删除数据，这在软件开发和系统设计中是至关重要的。

## 1.3 数据结构的分类

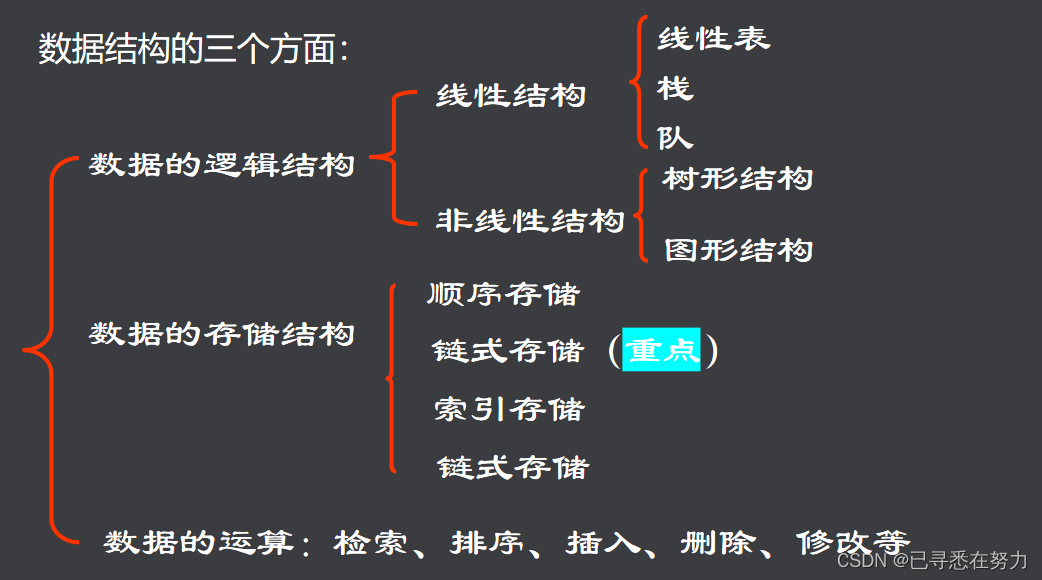
数据结构按其逻辑结构可以分为线性结构和非线性结构。线性结构包括数组、链表、栈、队列等，它们之间的元素存在一对一的关系。而非线性结构则包含树、图等，元素之间存在一对多或多对多的关系。接下来，我们将深入探索这些结构，并了解它们在解决实际问题中的应用。

# 2. 线性结构在清华题中的应用

## 2.1 数组和链表的理论基础

### 2.1.1 数组的概念及其在清华题中的应用

数组是计算机科学中最基本的数据结构之一，它由一系列相同类型的元素构成，这些元素使用连续的内存空间进行存储。在清华大学的算法与数据结构课程中，数组常常被用于解决各种问题，比如动态规划、排序算法等。

在解决相关问题时，我们使用数组来存储临时数据或最终结果。例如，在解决最大子序列和问题（也称为最大子数组问题）时，我们通常使用一个数组来存储到当前位置为止的最大子序列和。算法的时间复杂度为O(n)，空间复杂度为O(1)（忽略返回结果所需的存储空间）。

#include <stdio.h>

// 函数用于找出数组中的最大连续子序列和
int maxSubArraySum(int a[], int size) {
    int max_so_far = a[0];
    int curr_max = a[0];
    for (int i = 1; i < size; i++) {
        curr_max = (a[i] > curr_max + a[i]) ? a[i] : curr_max + a[i];
        max_so_far = (max_so_far > curr_max) ? max_so_far : curr_max;
    }
    return max_so_far;
}

int main() {
    int arr[] = {-2, -3, 4, -1, -2, 1, 5, -3};
    int n = sizeof(arr) / sizeof(arr[0]);
    int max_sum = maxSubArraySum(arr, n);
    printf("Maximum contiguous sum is %d\n", max_sum);
    return 0;
}

在这个例子中，`maxSubArraySum` 函数利用数组存储计算的最大连续子序列和。每一步中，我们都更新当前的最大值 `curr_max` 和全局的最大值 `max_so_far`。这种方法是典型的动态规划思路，利用数组记录历史信息，从而达到优化算法的目的。

数组在算法设计中扮演着重要的角色，尤其是在需要随机访问元素时，数组的特性能够极大地提升算法的效率。在清华大学的编程题目中，通过数组这种数据结构，我们可以快速解决需要频繁访问、更新数据的问题。

### 2.1.2 链表的原理及其在清华题中的应用

与数组不同，链表是一种物理上非连续、通过指针链接的线性数据结构。链表中的每个节点包含两个部分：一部分是存储数据的单元，另一部分是指向下一个节点的指针。在解决清华大学的编程问题时，链表可以用来模拟某些动态数据的场景，如实现队列、堆栈等数据结构。

链表在处理动态数据集合时具有很大的灵活性。例如，在需要在列表中间频繁插入和删除节点的情况下，使用链表可以比使用数组更加高效，因为插入和删除操作链表仅需要移动指针，而数组则需要移动所有相关元素。

下面是一个实现单链表数据结构的简单代码示例：

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点结构体
struct Node {
    int data;
    struct Node* next;
};

// 创建新节点的函数
struct Node* createNode(int data) {
    struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

// 插入节点到链表的末尾的函数
void append(struct Node** head_ref, int data) {
    struct Node* newNode = createNode(data);
    struct Node* last = *head_ref;

    if (*head_ref == NULL) {
        *head_ref = newNode;
        return;
    }

    while (last->next != NULL) {
        last = last->next;
    }

    last->next = newNode;
}

// 打印链表的函数
void printList(struct Node* node) {
    while (node != NULL) {
        printf("%d -> ", node->data);
        node = node->next;
    }
    printf("NULL\n");
}

// 释放链表内存的函数
void freeList(struct Node** head_ref) {
    struct Node* current = *head_ref;
    struct Node* next;

    while (current != NULL) {
        next = current->next;
        free(current);
        current = next;
    }
    *head_ref = NULL;
}

int main() {
    struct Node* head = NULL;
    append(&head, 6);
    append(&head, 7);
    append(&head, 8);
    printList(head);
    freeList(&head);
    return 0;
}

在这个示例中，`append` 函数将新节点添加到链表的末尾，而`printList` 函数用于输出链表的所有元素。链表的这些操作都是通过指针操作完成的，对于需要动态增长或缩减的数据集，链表能够提供更优的性能。

在清华大学的算法题中，链表通常用于实现如循环链表、双向链表等更复杂的结构，以解决各种数据组织和检索问题。通过灵活地运用链表节点的插入和删除操作，我们可以对数据进行有效的管理，实现快速的数据存取。

# 3. 树结构在清华题中的应用

在数据结构中，树是一种非常重要的非线性数据结构，它被广泛应用于各种计算问题中，特别是在需要快速查找、插入和删除等操作的场景中。本章节将深入探讨树结构在解决清华题目中的应用，从基本的二叉树到高级树结构如B树、B+树、红黑树和堆结构，通过具体的应用案例，引导读者更好地理解和掌握这些高级数据结构。

## 3.1 二叉树的深入分析

### 3.1.1 二叉树的概念和性质

二叉树是每个节点最多有两个子树的树结构，通常子树被称作“左子树”和“右子树”。二叉树在算法设计和数据组织方面有着广泛的应用。其重要的性质之一是，对于任意一个二叉树，若其深度为k，则至少含有k个节点。这也说明了二叉树在存储空间上的优势，特别是在高度平衡的情况下。

二叉树的遍历是算法设计中常见的操作，包括前序遍历（根节点 -> 左子树 -> 右子树）、中序遍历（左子树 -> 根节点 -> 右子树）和后序遍历（左子树 -> 右子树