机器学习：指数族分布与共轭先验

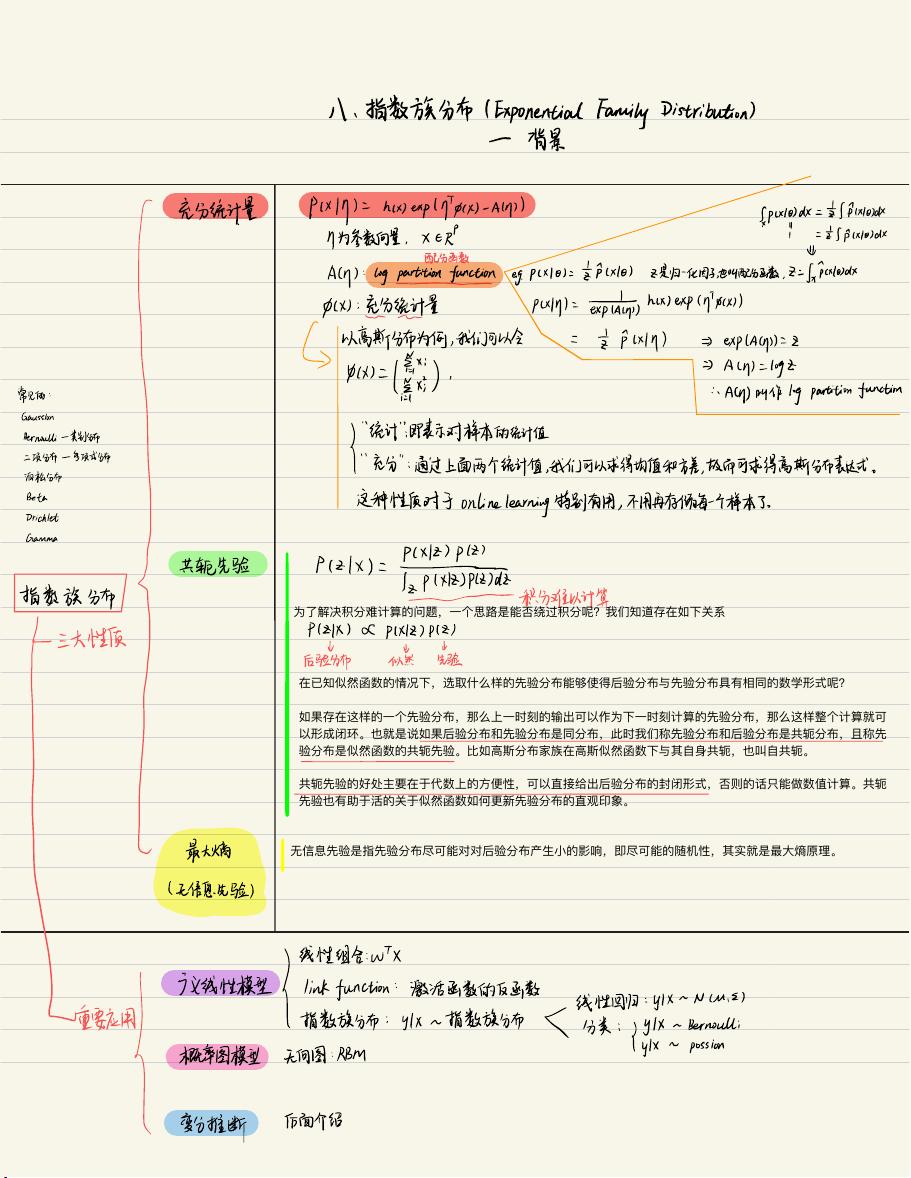
"这篇内容是关于机器学习中的指数族分布，它是概率论和统计学中的一个重要概念，尤其在机器学习算法推导中占有关键地位。指数族分布包括高斯分布、泊松分布等常见分布，它们具有特定的数学形式，便于进行统计推断和计算。充分统计量在此类分布中起着核心作用，可以用来简洁地概括数据的主要特征。" 在机器学习中，指数族分布是一类具有广泛应用的概率分布，其特点是可以通过一个共同的函数形式来表示，这个函数就是所谓的配分函数。配分函数是归一化的，确保了概率分布的总和为1。例如，高斯分布（正态分布）就是一个典型的指数族分布，其参数通常包括均值和方差。 描述中提到，充分统计量是指数族分布的一个关键概念，它可以将复杂的样本数据压缩为少数几个统计量，而不丢失任何关于原始数据的重要信息。例如，在高斯分布中，均值和方差就是充分统计量，它们可以完全确定一个高斯分布。通过这两个统计量，我们可以得到高斯分布的具体表达式。 共轭先验在贝叶斯统计中是非常重要的，它简化了计算过程。当一个先验分布与似然函数属于同一指数族时，它们的后验分布会保持相同的数学形式，这被称为共轭性。比如，如果似然是高斯分布，选择高斯先验就会得到高斯后验，这就是高斯分布的自共轭特性。共轭先验的优势在于可以得到后验分布的闭合形式，避免了数值积分的复杂性，有助于直观理解似然函数如何影响先验分布的更新。 无信息先验是一种弱假设的先验分布，它尽可能地对后验分布影响最小，使得模型更依赖于观测数据，而不是先验知识。这种先验通常基于最大熵原理，意味着在没有其他信息的情况下，选择最大化熵的分布。 此外，指数族分布还涉及到线性组合和广义线性模型。在这些模型中，指数族分布常被用作响应变量的概率分布，而线性组合（如线性函数或激活函数的反函数）则用来连接模型的预测值和这些指数族分布的参数。 最后，变分推断是处理复杂概率模型的一种方法，尤其是在指数族分布下，它能有效地近似后验分布，对于大规模数据集的学习尤其有用，因为它可以减少计算复杂度，不需要存储每个样本的信息。 指数族分布是机器学习算法中不可或缺的一部分，它们在贝叶斯推断、统计建模和优化计算等方面发挥着重要作用。理解并熟练运用指数族分布及其特性，对于提升机器学习模型的性能和效率至关重要。