Matlab环境下的短时交通流预测：小波变换与灰色马尔可夫模型

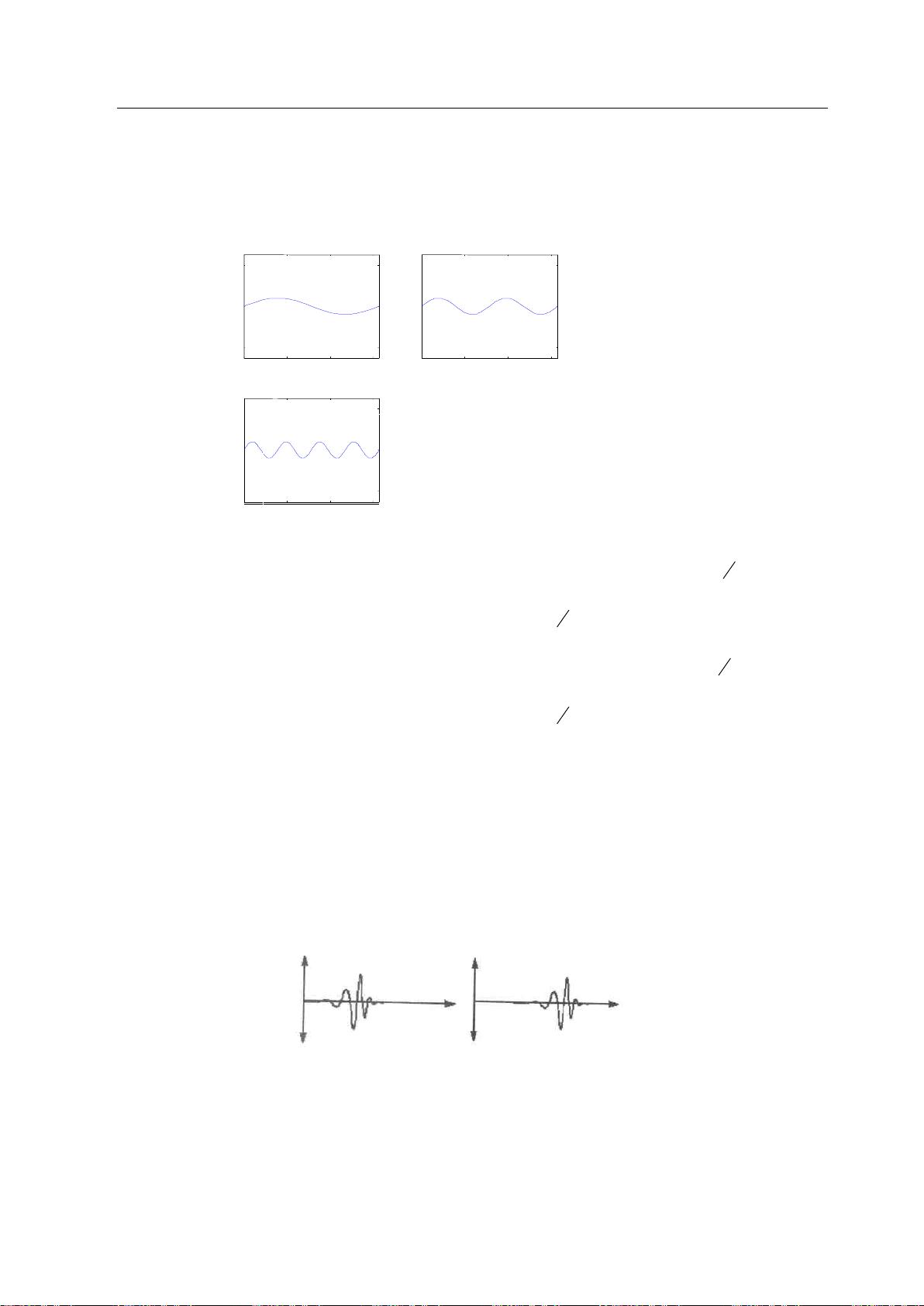
"这篇硕士论文主要探讨了基于Matlab的短时交通流预测方法，结合了小波变换和灰色马尔可夫模型。作者详细介绍了小波变换的基础，特别是Mallat分解与重构算法，以及灰色马尔可夫预测模型的理论。论文提出了一种新的预测模型，该模型首先使用db5小波对原始交通流数据进行分解，然后对重构后的近似部分应用灰色马尔可夫模型进行组合预测。通过GM(1,1)模型对数据进行拟合和预测，再利用加权马尔可夫链处理拟合残差，以提高预测精度。论文的数据来源于山东省泰安市东岳大街邮电局岗东向的交通流监测。实验结果表明，这种方法相比直接在原始数据上建模，能提供更高的预测精度，并且马尔可夫模型能有效补充灰色模型的不足，提升预测的准确性。关键词包括交通流预测、小波变换、灰色模型和加权马尔可夫预测模型。" 这篇论文深入研究了交通流量预测这一关键问题，特别是在构建交通诱导系统和智能交通系统中的作用。它侧重于短期交通流量的预测，这是交通管理中极具挑战性的任务。作者首先介绍了小波变换，这是一种强大的信号处理工具，可以分解复杂的数据并揭示其不同时间尺度上的特性。Mallat分解与重构算法是小波分析的一部分，它允许数据在不同分辨率下进行分析和重组。 接着，论文讨论了灰色马尔可夫模型，这是一种适用于非完整或不完全信息系统的预测方法。在Matlab环境下，论文提出了一种创新的预测模型，它将Daubechies-5小波变换与灰色马尔可夫模型相结合。通过db5小波的五级分解，原始交通流数据被拆分成近似部分和细节部分，近似部分用于建立灰色马尔可夫模型。论文利用GM(1,1)单因素模型对重构后的数据进行拟合和预测，然后分析残差以确定状态转移概率。 论文还引入了加权马尔可夫链，通过对拟合残差进行“马氏性”检验，确保数据满足预测条件。通过计算各阶自相关系数和状态转移概率，确定了权重，以此优化预测过程。加权状态转移概率的最大值指示了下一个信号周期交通流量预测的残差状态。 实证研究部分，论文使用来自山东省泰安市的200个连续信号周期的交通流数据，验证了组合预测模型的有效性。实验结果显示，这种结合小波变换和灰色马尔可夫模型的方法在预测精度上优于直接使用原始数据的模型，并且马尔可夫模型能够有效地改善灰色模型的预测残差，从而提高总体预测准确性。 这篇论文为短时交通流预测提供了一个新的方法，它融合了小波变换的精细分析能力和灰色马尔可夫模型的适应性，为交通管理提供了更准确的预测工具，有助于优化交通流的规划和控制。