Python编程中非均匀随机数生成的多种方法

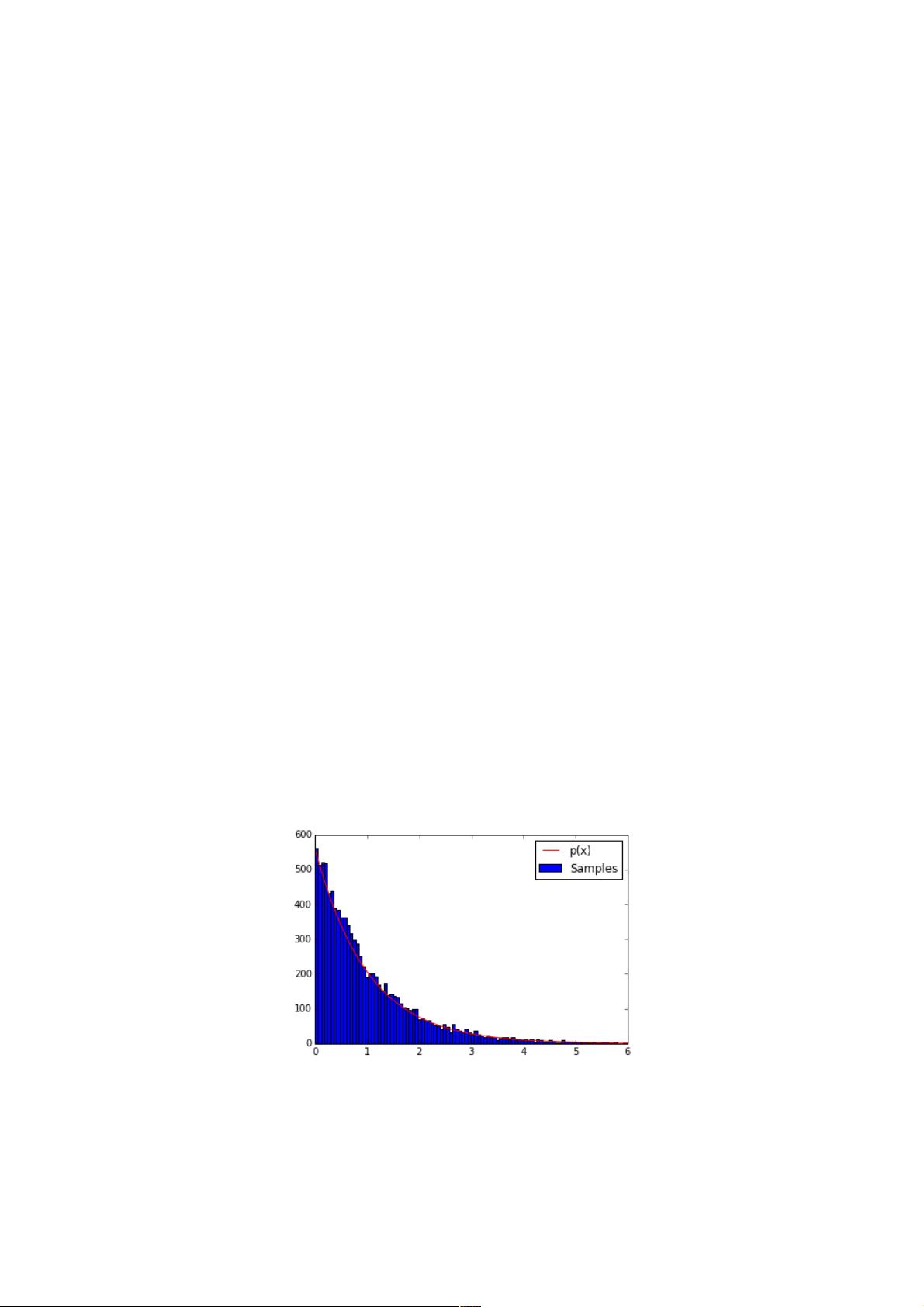
Python编程产生非均匀随机数的几种方法代码分享 本文主要介绍了Python编程中产生非均匀随机数的几种方法代码分享，具有一定借鉴价值，需要的朋友可以参考下。 **反变换法** 反变换法是产生非均匀随机数的一种常用方法。设需产生分布函数为F(x)的连续随机数X。若已有[0,1]区间均匀分布随机数R，则产生X的反变换公式为：F(x)=r，即x=F^-1(r)。在这种方法中，我们首先需要得到分布函数F(x)的反函数，然后使用均匀分布随机数R来生成非均匀随机数X。 在Python中，我们可以使用NumPy和Matplotlib库来实现反变换法。例如，下面的代码使用反变换法在区间[0,6]上生成随机数，其概率密度近似为P(x)=e^-x： ``` import numpy as np import matplotlib.pyplot as plt # 概率分布我们尝试计算 p = lambda x: np.exp(-x) # CDF of p CDF = lambda x: 1 - np.exp(-x) # invert the CDF invCDF = lambda x: -np.log(1 - x) # 域限 xmin = 0 # 下限 xmax = 6 # 上限 # 范围限制 rmin = CDF(xmin) rmax = CDF(xmax) N = 10000 # 总样本数 # 生成均匀样本在我们的范围内，然后invert the CDF # 来获取目标分布的样本 R = np.random.uniform(rmin, rmax, N) X = invCDF(R) # 获取histogram信息 hinfo = np.histogram(X, 100) # 绘制histogram plt.hist(X, bins=100, label=u'Samples'); # 绘制我们的（normalized）函数 ``` **反函数存在条件** 在反变换法中，需要注意反函数的存在条件。如果函数y=f(x)是定义域D上的单调函数，那么f(x)一定有反函数存在，且反函数一定是单调的。分布函数F(x)是一个单调递增函数，所以其反函数存在。 **概率密度函数** 在反变换法中，我们需要知道概率密度函数P(x)。在上面的例子中，我们使用了指数分布的概率密度函数P(x)=e^-x。我们可以根据实际情况选择合适的概率密度函数。 **Matplotlib库** 在上面的例子中，我们使用了Matplotlib库来绘制histogram和函数图像。Matplotlib库是一个非常强大的数据可视化库，可以用来绘制各种类型的图表。 **NumPy库** 在上面的例子中，我们使用了NumPy库来实现数学运算。NumPy库是一个非常强大的科学计算库，提供了大量的数学函数和数组操作。 反变换法是一种非常有用的方法，可以用来产生非均匀随机数。通过使用Python语言和相关库，我们可以轻松地实现反变换法，并且获得所需的随机数。