深度学习：克服神经网络局限性的策略

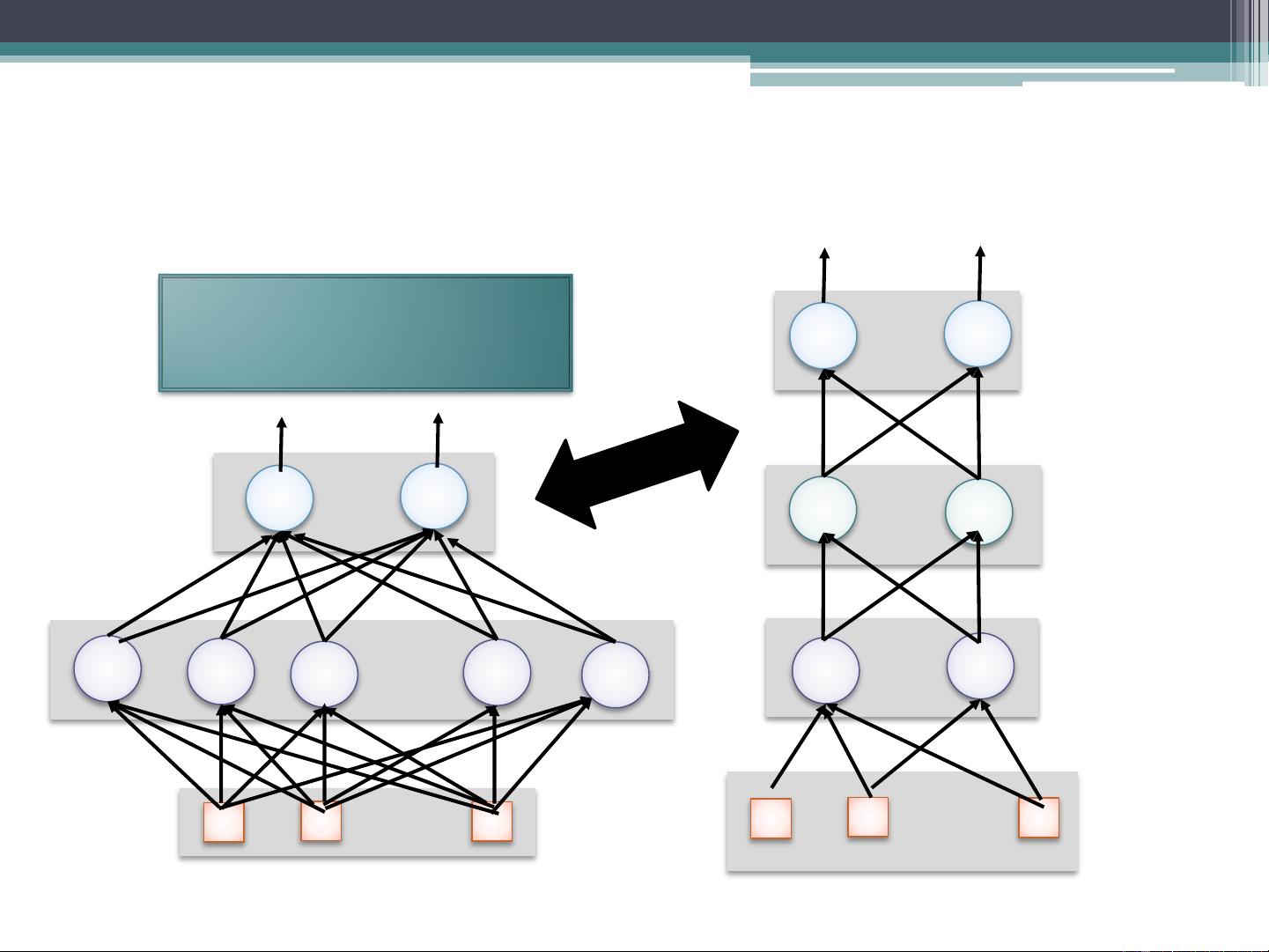
"这篇资源详细介绍了人工智能领域中的深度神经网络（Deep Neural Networks），由Dong Xu在EECS Department、C.S. Bond Life Sciences Center和Informatics Institute的讲座中提出。内容涵盖深度架构的动机、输入表示、softmax函数、激活函数如maxout和ReLU，以及dropout技术。同时，讨论了神经网络的局限性，包括随机初始化和密集连接导致的高昂成本、随着隐藏层增加训练难度增大、梯度消失问题、局部最优陷阱等。此外，还提到了生物启发的深度学习概念，指出人脑的结构与深度神经网络有相似之处。" 正文: 深度神经网络（Deep Neural Networks，简称DNN）是人工智能领域的重要组成部分，它模拟了人脑神经元的工作方式，通过多层非线性变换对复杂数据进行建模和处理。DNN的核心在于其深度，即包含多个隐藏层，这使得网络能够学习更高级别的抽象特征。 **深度架构的动机** 深度架构的出现是为了处理高维度和复杂的输入数据，例如图像、语音和文本。每一层神经网络可以捕获不同级别的特征，底层捕获基本特征，高层则捕获更抽象的概念。这种逐层学习有助于提高模型的泛化能力。 **输入表示** 输入表示是深度学习的第一步，如何将原始数据转化为神经网络可以理解的形式至关重要。这可能包括特征提取、预处理和标准化等步骤，确保输入数据适合网络的训练。 **softmax与分类** softmax函数常用于多分类问题的输出层，它将神经网络的最后一层输出转换为概率分布，确保所有类别的概率之和为1，从而便于选择最可能的类别。 **激活函数** 激活函数如maxout和ReLU（Rectified Linear Unit）是神经网络非线性的来源。ReLU函数在正区间的线性特性解决了传统Sigmoid和Tanh函数的梯度消失问题，提高了网络的训练效率。Maxout则是ReLU的扩展，通过取多个线性单元的最大值来增加网络的表达能力。 **dropout技术** dropout是一种正则化方法，它在训练过程中随机关闭一部分神经元，防止过拟合并促进模型的泛化性能。通过这种方式，每个神经元被迫学习更通用的特征，而不是依赖于特定的神经元组合。 **神经网络的局限性** 尽管深度神经网络表现出色，但它们也存在一些挑战。随机初始化和密集连接可能导致训练成本高昂，因为每个神经元都可以看作一个逻辑回归模型，需要大量计算资源。随着隐藏层数的增加，梯度下降法在反向传播时遇到梯度消失问题，使得深层节点的参数调整困难。此外，由于目标函数通常是非凸的，网络可能会陷入局部最优或鞍点，训练过程可能停滞不前。 **生物启发** 深度学习的灵感来源于人脑的神经生物学结构，大脑的皮层层次结构与DNN的多层设计相呼应，每一层处理不同的认知任务。这为深度学习提供了一个生物可行性的解释，并推动了更多基于生物灵感的网络结构和优化算法的研究。 总结来说，深度神经网络是现代人工智能的关键技术，它通过多层次的学习来处理复杂的数据。然而，克服训练成本、梯度消失和局部最优等问题，以及进一步理解生物神经网络的工作机制，仍然是深度学习研究的重要方向。