频率域图像处理：滤波与增强技术解析

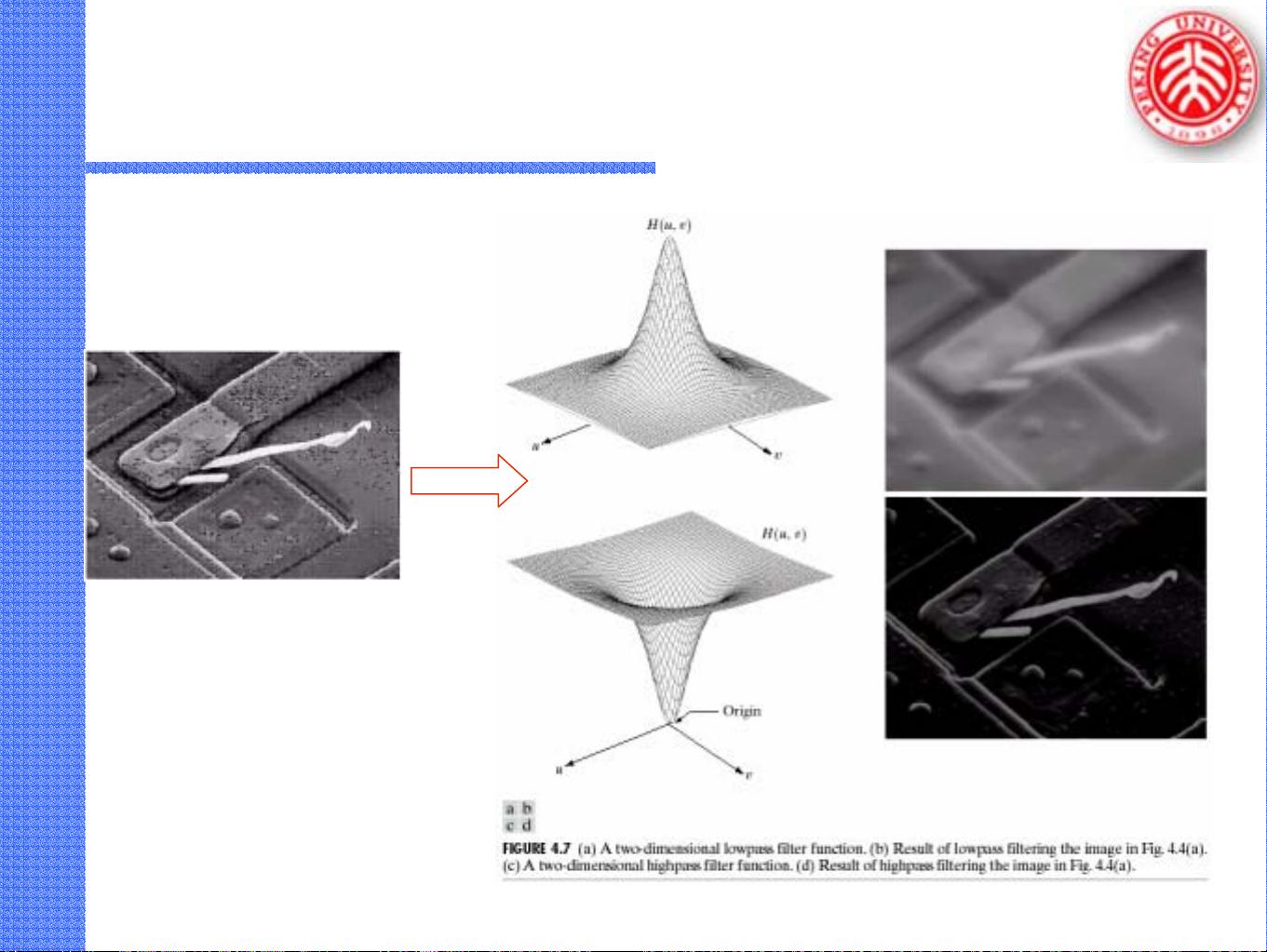
"本资料主要讲解了图像处理中的频率域滤波技术，包括频率域图像增强、频率域滤波器以及滤波步骤。由北京大学计算机科学技术研究所的彭宇新教授提供，适用于研究生级别的数字图像处理课程学习。" 在图像处理领域，频率域滤波是一种重要的技术，它基于傅里叶变换理论，对图像的频率成分进行操作以达到增强或平滑的效果。傅里叶变换将图像从空间域转换到频率域，使得图像的高频成分代表图像的细节（如边缘和噪声），而低频成分则对应图像的整体亮度和大范围的平滑区域。 频率域图像增强是图像处理中的一个重要概念，因为它允许我们根据图像的频率特性进行有针对性的调整。在空间域中，某些图像增强任务可能复杂且难以表达，但在频率域中，这些任务可以变得简单易懂。例如，通过选择性地增强或抑制特定频率成分，我们可以有效地平滑图像（低通滤波）或锐化图像（高通滤波）。频率域处理提供了实验和调整滤波器参数的便利，这在寻找最佳滤波效果时非常有用。一旦找到合适的滤波器，通常会在空间域中通过硬件实现以提高处理速度。 傅里叶变换是频率域分析的基础，它将图像的每个像素位置(x, y)映射到频率坐标(u, v)。变换的中心点(u = 0, v = 0)对应图像的平均灰度，低频成分对应图像的缓慢变化区域，而高频成分则对应快速变化的区域，如边缘和噪声。通过分析和修改这些频率分量，我们可以对图像进行各种增强操作。 频率域滤波通常包括以下步骤：首先，对图像进行中心变换；然后计算傅里叶变换；接着，将滤波器函数H与傅里叶变换结果相乘；再进行反傅里叶变换；最后，取消输入图像中心变换的乘数，得到最终的处理图像。滤波器函数H的设计至关重要，它可以是低通、高通或其他类型的滤波器，用于实现不同的图像处理目的。 滤波器H与傅里叶变换F的乘法是在元素级别进行的，F的复数元素与H的实数元素相乘。零相移滤波器H不会改变变换的相位，因此在乘法过程中可以消除F的虚部和实部的相位差，简化滤波过程。 频率域滤波的基本步骤还包括计算相位角，这对于理解滤波后图像的相位变化和恢复图像的原始结构至关重要。频率域滤波是图像处理中的核心技术，它为理解和改善图像质量提供了强大的工具。