提升理解的视觉指南：线性代数的几何含义

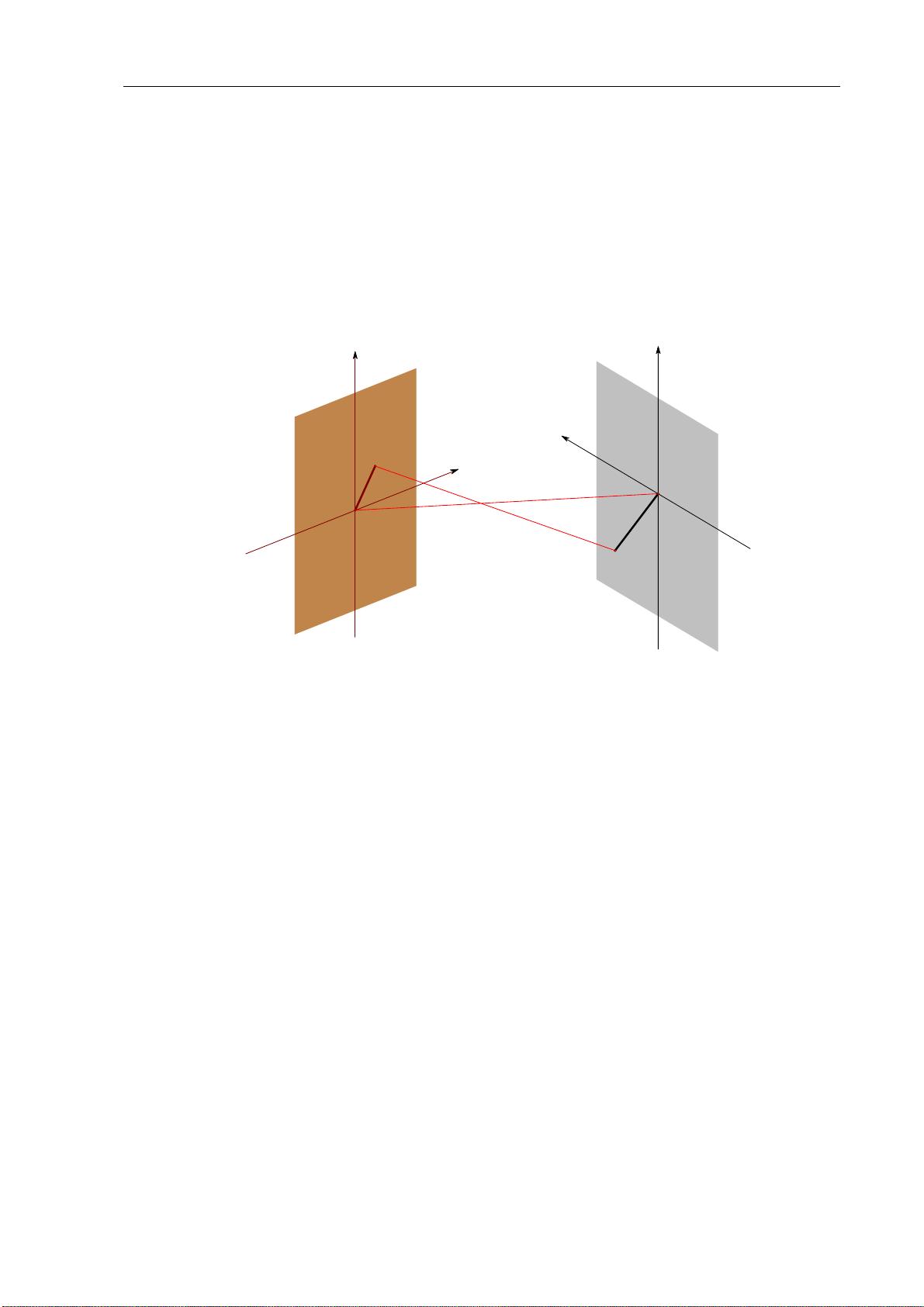
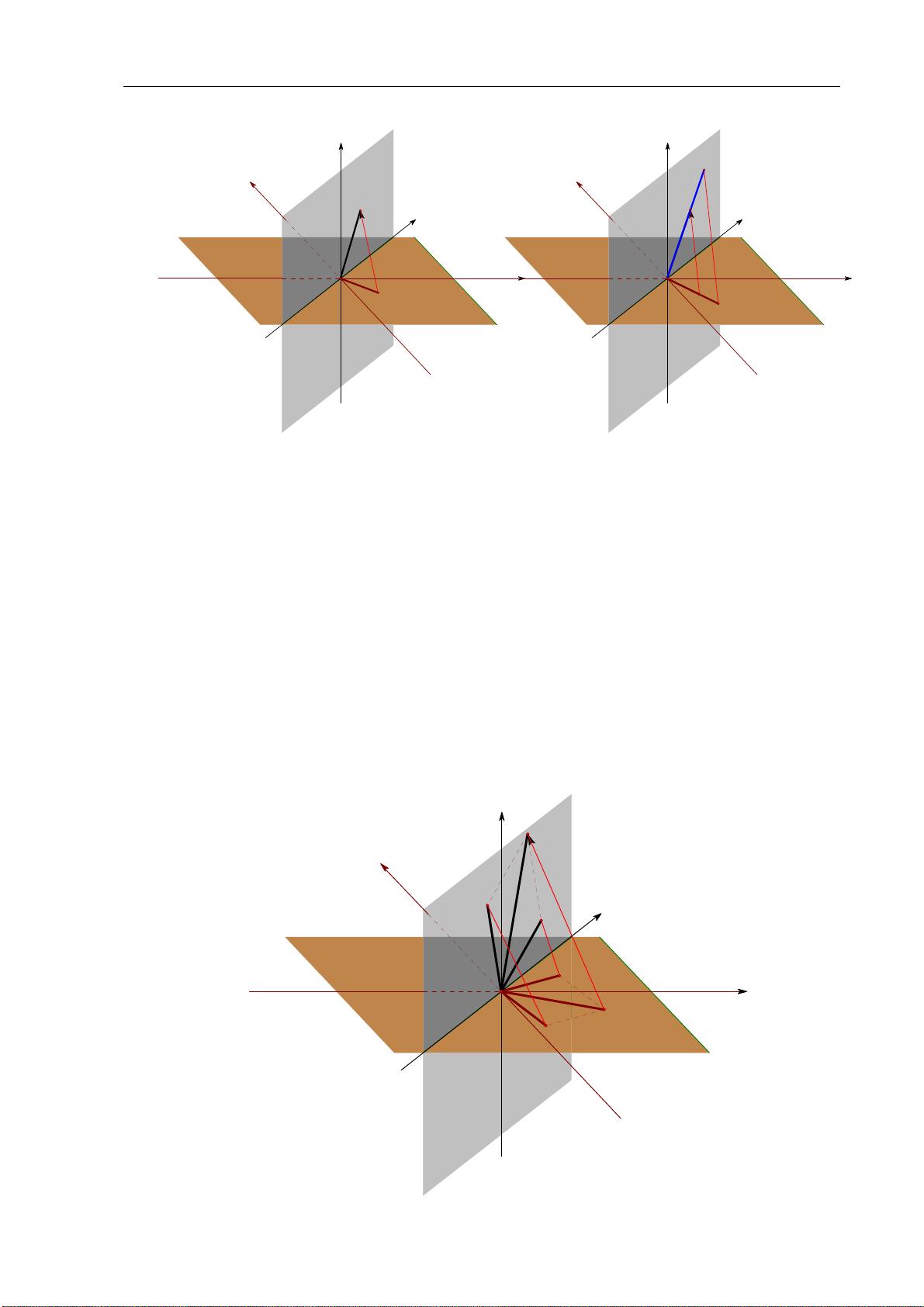
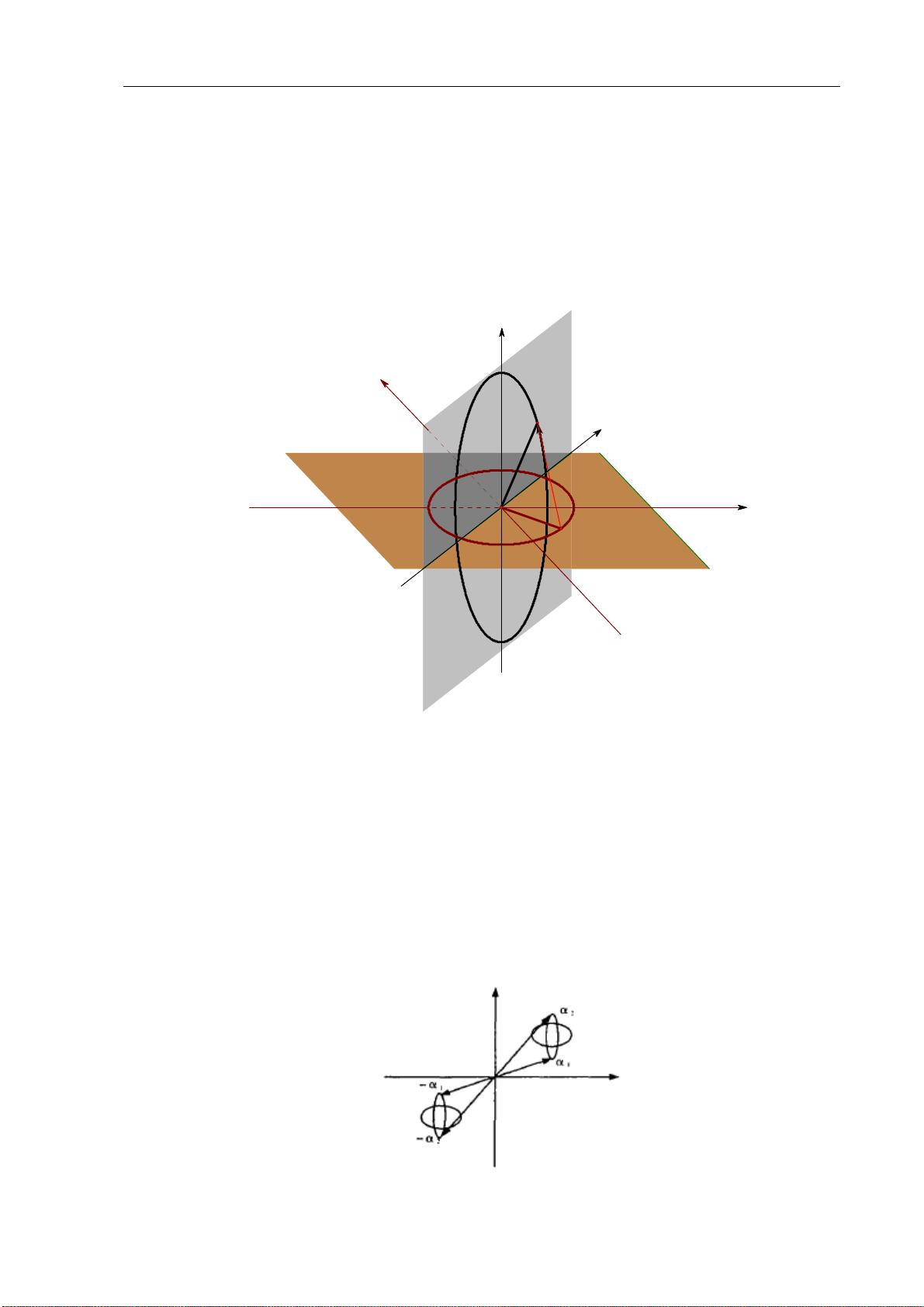
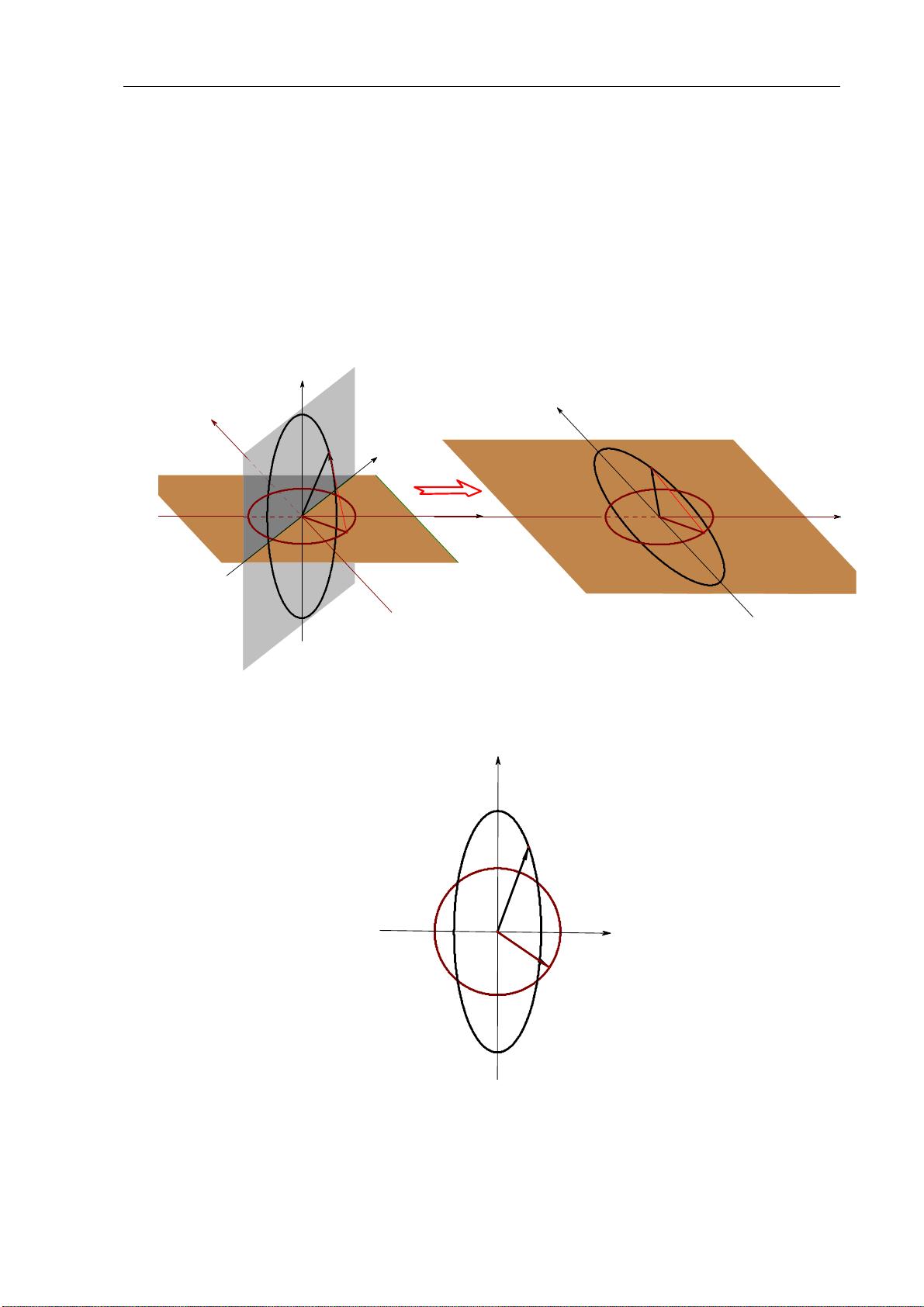
线性代数是一门基础且广泛应用的数学分支，它将抽象的数学术语与直观的几何概念紧密结合，使得难以理解的概念变得生动易懂。几何意义在学习线性代数中扮演着至关重要的角色，它不仅增强了理论知识的可视化，还极大地促进了实际问题的理解和解决。 首先，线性代数中的向量和空间观念与几何图形有着直接对应。向量可以看作是有方向和大小的箭头，它们在二维或三维空间中的表示，如坐标系中的点或平面向量，直观地反映了线性关系。矩阵则可以被视作变换空间的工具，通过矩阵乘法，我们可以进行平移、旋转、缩放等几何操作，这些都是图形学和计算机图形的基础。 其次，几何意义对于图像处理尤为重要。例如，在计算机视觉中，像素矩阵被处理为线性变换，通过矩阵运算实现图像的滤波、特征提取和识别。此外，特征值和特征向量的概念可以用来描述图像的不变性，即使在缩放、旋转或平移后，关键特征依然保持不变。 希尔伯特的名言强调了几何和代数结合的重要性，他认为两者的发展相辅相成，几何图形的直观性能够推动代数的进步，反之亦然。拉格朗日的言论表明，几何直觉对于数学思维至关重要，缺乏几何视角的人可能会在解决问题时遇到困难。 徐利治这位数学家的观点则从教育的角度强调了直观理解在学习过程中的价值，他认为理解数学定理和证明的几何含义是掌握知识的关键。这提醒我们，线性代数的学习不应仅仅停留在符号和公式层面，而应尽可能地与几何直观结合起来。 在实际工程应用中，许多电子工程师发现数学能力，特别是线性代数，对于高级技术理解和问题解决是必不可少的。然而，当面对复杂的数学概念时，如果没有深入的几何理解，他们可能会感到困惑和挫败。因此，了解线性代数的几何意义，可以帮助工程师们提升数学素养，更好地应对工作中的挑战。 线性代数的几何意义不仅提供了更深刻的理解框架，而且是提高数学技能、促进工程实践的重要途径。通过将抽象的数学概念与直观的几何图形相结合，我们可以更好地应用线性代数于各种领域，包括科学计算、数据分析、机器学习以及图形和图像处理。