JavaScript中的精确浮点数打印：全面且性能优化的方法
11 浏览量
更新于2024-08-25
收藏 564KB PDF 举报
"《打印浮点数：一个始终正确的方法》（fp-printing-popl16）是一篇由Marc Andrysco、Ranjit Jhala和Sorin Lerner三位来自美国加州大学圣地亚哥分校的专家合作撰写的论文。该文章聚焦于在现代软件中，特别是在JavaScript中日益重要的浮点数处理问题。浮点数作为计算中的基本组成部分，其转换成可读的十进制形式是必不可少的，但现有的转换算法往往在完整性和性能之间存在权衡。
传统的Dragon4算法，由Steele和White提出并进一步优化，旨在实现完全性，即在所有输入上都能产生正确且最优的输出。它依赖于任意精度的整数运算（大数算术），这虽然保证了转换的准确性，但会带来显著的性能开销。这意味着在追求精确性的同时，可能会牺牲速度。
另一方面，文中提到的Grisu3算法是近期的一种改进，它的出现可能是为了平衡精度与效率。Grisu3算法可能采用了不同的策略，例如使用更高效的算法或近似方法，来减少大数计算的需求，从而在一定程度上提高转换速度，但可能在某些情况下无法达到Dragon4那样的严格完备性。
本文的核心贡献在于提出了一种总是正确的浮点数打印方法，它在保证转换准确性的前提下，尽可能地优化了性能。作者详细讨论了设计决策、算法实现以及评估过程，使得读者不仅能理解其技术原理，还能方便地复用和评估这种技术。由于其在Web环境中的重要性，这篇论文不仅对于软件开发者和数值计算研究者具有很高的价值，也为实际应用中的浮点数表示提供了一种实用且可靠的解决方案。"
ñ⁺
m ⁺
v
w ⁺
w ⁻
m ⁻
ñ⁻
narrow interval
rounding interval
wide interval
uncovered intervals
v ⁺
v ⁻
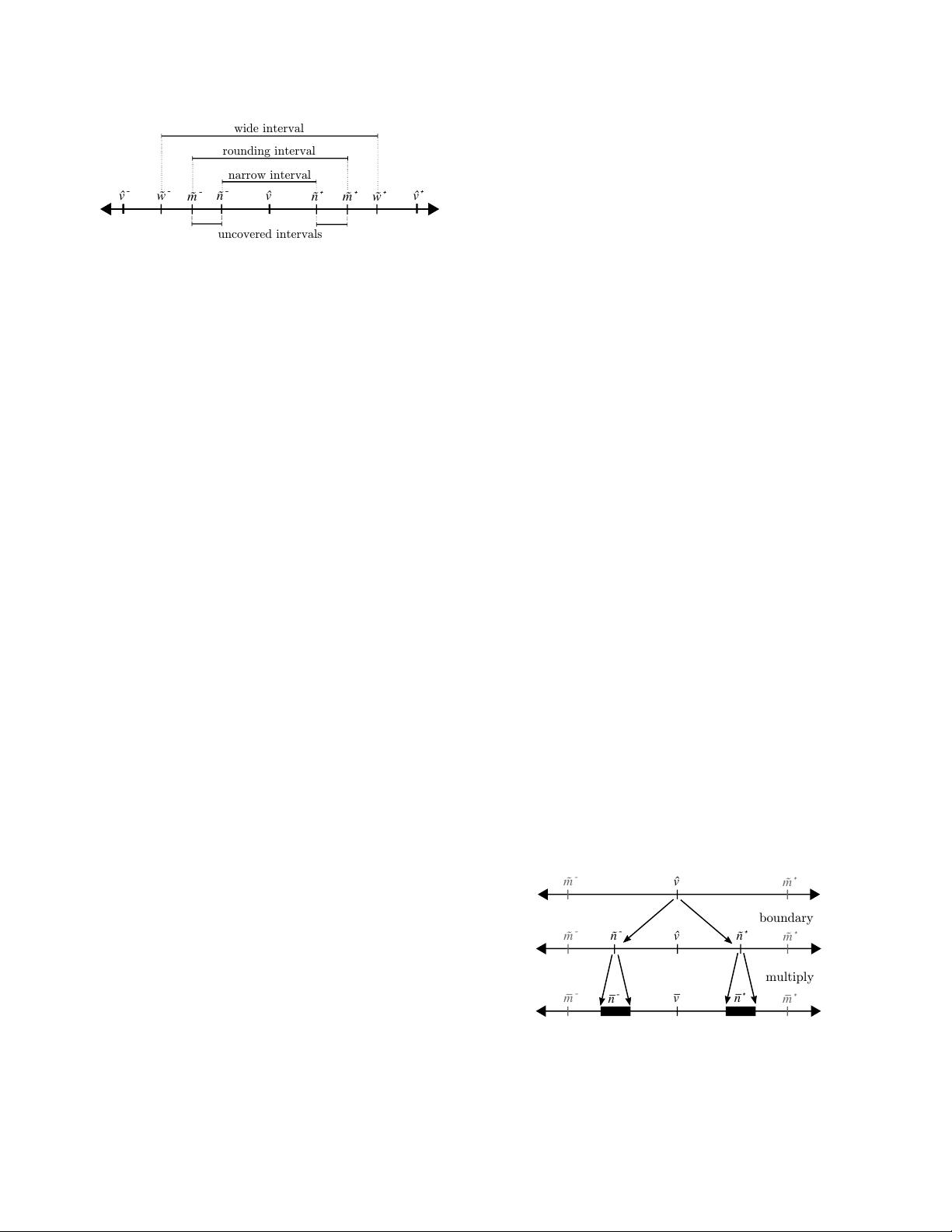
Figure 1: Representations, Midpoints and Boundaries: ˆv denotes a
native, machine representable floating point number with neighbors
ˆv
−
and ˆv
+
; ˜m
−
and ˜m
+
denote exact midpoints; ˜n
−
and ˜n
+
denote the narrow (or conservative) boundaries; ˜w
−
and ˜w
+
denote
wide boundaries; and the uncovered intervals denote the portion of
the rounding interval not covered by the narrow interval.
•
Step 1: Compute narrow boundaries ˜n
−
, ˜n
+
such that:
˜m
−
< ˜n
−
< ˆv < ˜n
+
< ˜m
+
•
Step 2: Compute shortest decimal in the interval [˜n
−
, ˜n
+
].
By relaxing the constraints of using exact midpoints ˜m
−
, ˜m
+
,
Grisu3 can use efficient operations over limited-precision numbers
(instead of Dragon4’s bignum) to yield provably correct albeit
possibly suboptimal conversions.
Scaled Narrow Intervals. A triple (e, ¯n
−
, ¯n
+
) is a scaled narrow
interval for ˆv if there exists ˜n
−
, ˜n
+
such that:
1. ¯n
+
∈ (1, 10]
2. ¯n
−
≈ 10
−e
× ˜n
−
3. ¯n
+
≈ 10
−e
× ˜n
+
4. ˜m
−
< ˜n
−
< ˆv < ˜n
+
< ˜m
+
Intuitively, a scaled narrow interval for ˆv corresponds to a narrow
interval for ˆv where the boundaries are scaled by 10
−e
to ensure
that the upper bound ¯n
+
is in (1, 10]. Note that the last requirement
allows us to compute the (scaled) narrow intervals approximately,
e.g. using HP numbers, as long as the (unscaled) boundaries reside
within the exact midpoints ˜m
−
and ˜m
+
. Finally, only the upper
boundary ¯n
+
must be in the interval (1, 10], hence we observe that
the exponent is e ≈ blog
10
˜n
+
c.
Algorithm. Figure 2 formalizes the above intuition in a generic
algorithm to convert an input FP value ˆv into decimal form
comprising a pair of a sequence of digits d
1
, . . . , d
N
and an ex-
ponent e denoting the decimal value 0.d
1
. . . d
N
× 10
e
. (Although
this differs slightly from the normal format – with a leading non-
zero digit – we can normalize by shifting the decimal point to
the right.) The convert algorithm is split into two procedures,
narrow_interval and digits, corresponding to the steps de-
scribed above. The first phase narrow_interval begins with
the input ˆv and computes a scaled narrow interval (e, ¯n
−
, ¯n
+
) for
ˆv. The second phase digits uses the scaled narrow interval to
compute the final output digits corresponding to the shortest dec-
imal value within the scaled narrow interval [¯n
−
, ¯n
+
]. Next, we
describe the two steps in detail.
3.2 Step 1: Compute Narrow Interval
The first phase computes the scaled narrow interval (e, ¯n
−
, ¯n
+
)
for the input ˆv. First, the (unscaled) boundary ˜n
−
, ˜n
+
is computed
directly from the input ˆv by the function boundary. Second, the
exponent e is directly computed from the upper boundary ˜n
+
by
scaling it to ensure that its significand lies in the range [1, 10). That
def convert(ˆv):
(e,¯n
−
,¯n
+
) = narrow_interval(ˆv)
digits = digits(¯n
−
,¯n
+
)
return (digits,e)
def narrow_interval(ˆv):
(˜n
−
,˜n
+
) = boundary(ˆv)
e = floor(log10(˜n
+
))
¯n
−
= multiply(˜n
−
, 10
−e
)
¯n
+
= multiply(˜n
+
, 10
−e
)
return (e,¯n
−
,¯n
+
)
def digits(¯n
−
,¯n
+
):
digits = []
repeat:
(¯n
−
,d
−
) = next_digit(¯n
−
)
(¯n
+
,d
+
) = next_digit(¯n
+
)
digits.append(d
+
)
until(d
−
!= d
+
)
return digits
def next_digit(¯n):
d = truncate(¯n)
¯n = multiply(¯n - d, 10)
return (¯n,d)
Figure 2: A Generic Conversion Algorithm
is, the exponent e is computed as the value blog
10
˜n
+
c. Finally,
using the exponent, the scaled narrow boundaries are computed by
multiplying the narrow boundaries by 10
−e
.
The functions boundary and multiply are deliberately left
abstract. However, any concrete implementations must take care to
ensure that despite errors introduced by rounding and propagation,
the overall output is indeed a valid narrow interval for ˆv. Conse-
quently, the narrow boundaries computed by boundary are cho-
sen in a conservative fashion – as shown in Figure 3 – so that de-
spite any rounding and propagation errors, the results remain within
the actual midpoints, and hence form a valid narrow interval.
m ⁻
m ⁺
v
m ⁻
m ⁺
v
ñ⁺
ñ⁻
boundary
m ⁻
m ⁺
v n
⁺
n ⁻
multiply
Figure 3: Error Propagation. The multiply operation computes the
scaled interval (¯n
−
, ¯n
+
) with error (as represented by the black
boxes), creating the requirement that the narrow interval (˜n
−
, ˜n
+
)
be conservative enough to prevent overlap with the scaled mid-
points ¯m
−
and ¯m
+
剩余12页未读，继续阅读
2021-04-22 上传
2016-01-13 上传
点击了解资源详情
2022-09-19 上传
2022-09-22 上传
2011-10-24 上传
2021-06-30 上传
2021-04-22 上传
2021-03-31 上传
weixin_38688550
- 粉丝: 7
- 资源: 912
我的内容管理
展开
最新资源
- HPUX 11i V3系统管理员指南
- DIV+CSS布局大全
- J2EE 设计开发编程
- Serial ATA 2.6 Specification
- ITIL-white
- 《LINUX与UNIX SHELL编程指南》读书笔记
- 单源最短路径问题的Dijkstra算法
- Oracle 10g R2 Concepts双语版
- 02 第四章 使用SQL语句.pdf
- spring2.5 reference
- API函数大全(32 Bit Section PowerBuilder API)
- 51汇编指令表，一目了然，希望大家多多交流学习
- Serial ATA Specification Rev. 2.5
- 01 第一~三章.pdf
- asp.net速成教程
- Understanding JTA
