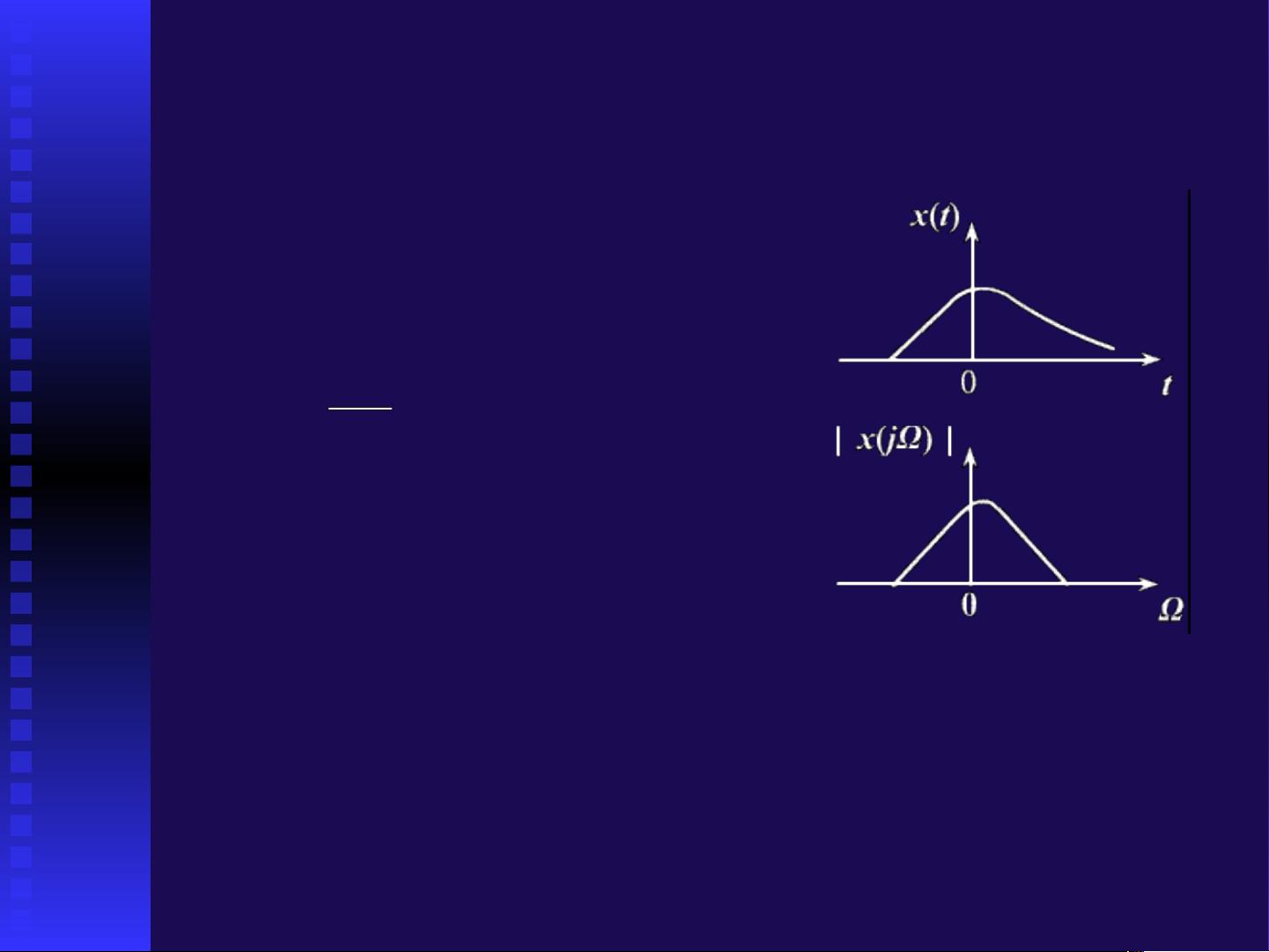离散傅里叶变换(DFT)详解及其应用

"数字信号处理第三章离散傅里叶变换" 在数字信号处理领域，离散傅里叶变换（DFT）是一个至关重要的概念，它在信号分析、滤波器设计、通信系统等多个方面都有广泛应用。本部分的学习目标旨在深入理解和掌握傅里叶变换的不同形式，特别是离散傅里叶变换及其相关性质。 1. Fourier变换的多种形式： - 连续时间、连续频率的傅里叶变换：适用于连续时间信号的分析，将信号从时域转换到频域，频谱是非周期的。 - 连续时间、离散频率的傅里叶级数：当连续时间信号是周期性时，其频谱表现为离散的频率分量。 - 离散时间、连续频率的序列傅里叶变换：针对离散时间信号的频谱分析，频域表现为周期延拓。 - 离散时间、离散频率的离散傅里叶变换（DFT）：在离散时间信号处理中最常用，时域和频域都是离散且周期的。 2. 周期序列的傅里叶级数及性质： - 周期序列可以表示为其傅里叶系数乘以正弦或余弦函数的和，这些系数代表了信号在不同频率成分的幅度。 - 周期卷积：两个周期序列的卷积在频域表现为乘法，这在信号处理中用于合并或滤波信号。 3. 离散傅里叶变换（DFT）及性质： - DFT将离散时间信号转换为离散频率的频谱，通过它可以分析信号的频率成分。 - 圆周移位：DFT的输入序列的移位在频域表现为频谱的相位变化。 - 共轭对称性：实数序列的DFT具有对称性，复数序列的DFT则具有共轭对称性。 - 圆周卷积：离散时间序列的卷积在频域对应于频谱的乘积，线性卷积可以通过两次圆周卷积和适当的移位来实现。 4. 频域抽样理论： - 在离散傅里叶变换中，频域的采样对应于时域的信号长度，频域的采样率决定了时域的分辨率。 5. 频谱分析过程： - 分析信号的频谱通常涉及DFT计算，通过观察DFT的结果可以了解信号的频率成分和强度。 6. 序列的抽取与插值： - 抽取（下采样）：减少数据点数，可能导致混叠现象，需保证奈奎斯特定理的要求。 - 插值（上采样）：增加数据点数，通过插值算法估计新位置的信号值，提高时域分辨率。 理解并熟练应用离散傅里叶变换及其相关性质，对于进行数字信号处理至关重要。通过对不同形式的傅里叶变换的理解，可以更有效地分析和处理各种类型的时间序列数据。