离散时间信号与系统的初步探索

"该资源是关于数字信号处理的第一讲，主要涵盖了离散时间信号与系统的基础概念和关键知识点。" 在数字信号处理中，离散时间信号，也称为序列，是通过对连续时间信号进行等间隔采样得到的。当模拟信号 xa(t) 以固定的采样间隔 T 进行采样时，我们得到一系列离散的样本值 xa(nT)，其中 n 是整数。简化表示，可以忽略采样间隔，将信号记作 x(n)，它代表第 n 个采样点的值。值得注意的是，x(n) 只在 n 为整数时才有定义。 序列的表示方法有多种。一个有限长的序列 x(n) 可以直接列出其所有元素，如 x(n) = {2, 1.2, -1.4, 3, 1, 4, 3.1, 7}。此外，序列也可以用向量来表示，其中 n 值对应向量的位置，而向量的元素则代表序列的数值。在 MATLAB 中，由于数组下标通常从 1 开始，所以序列 x(n) 可能会以 x = [2, 1.2, -1.4, 3, 1, 4, 3.1, 7]' 的形式表示。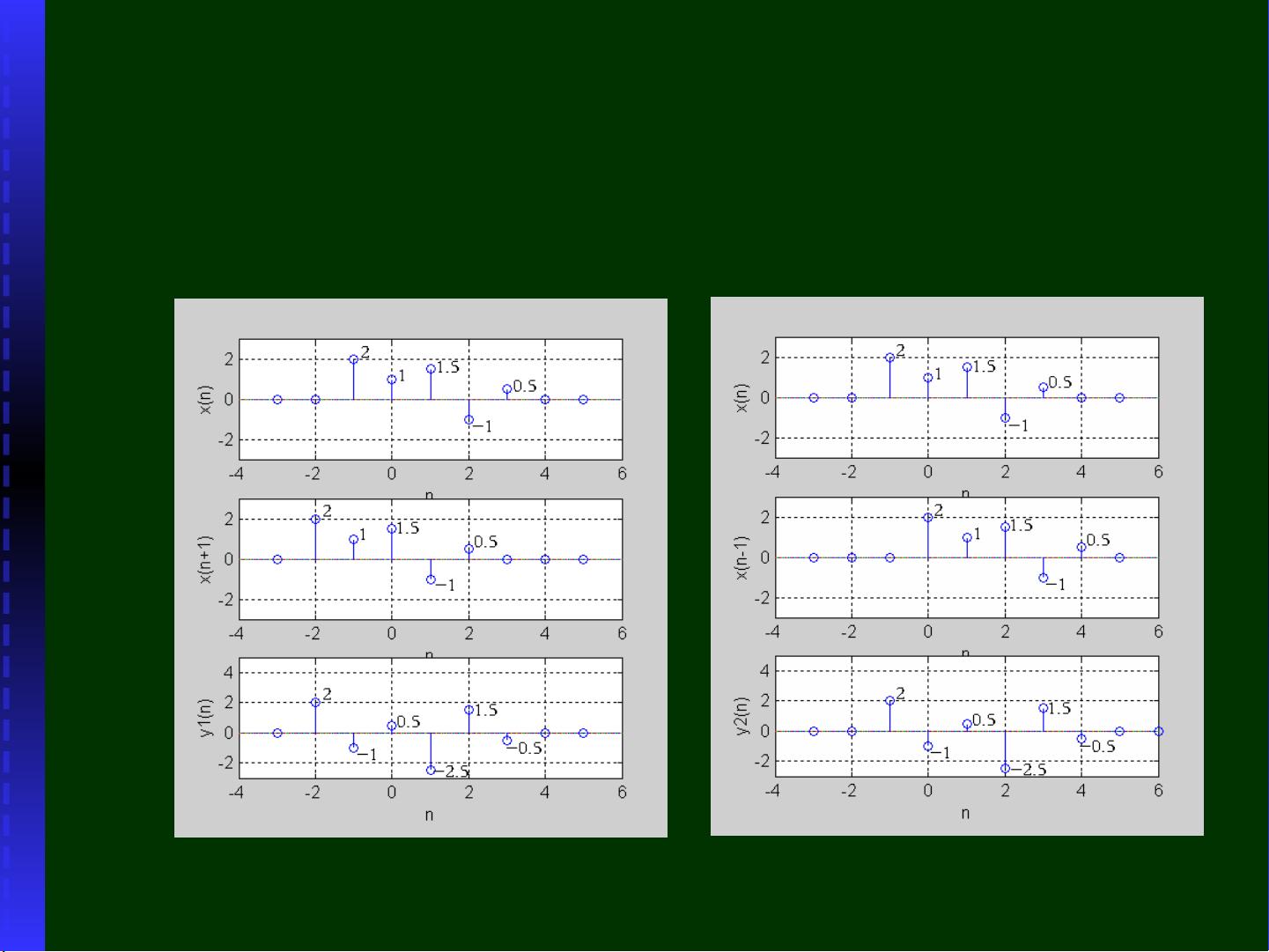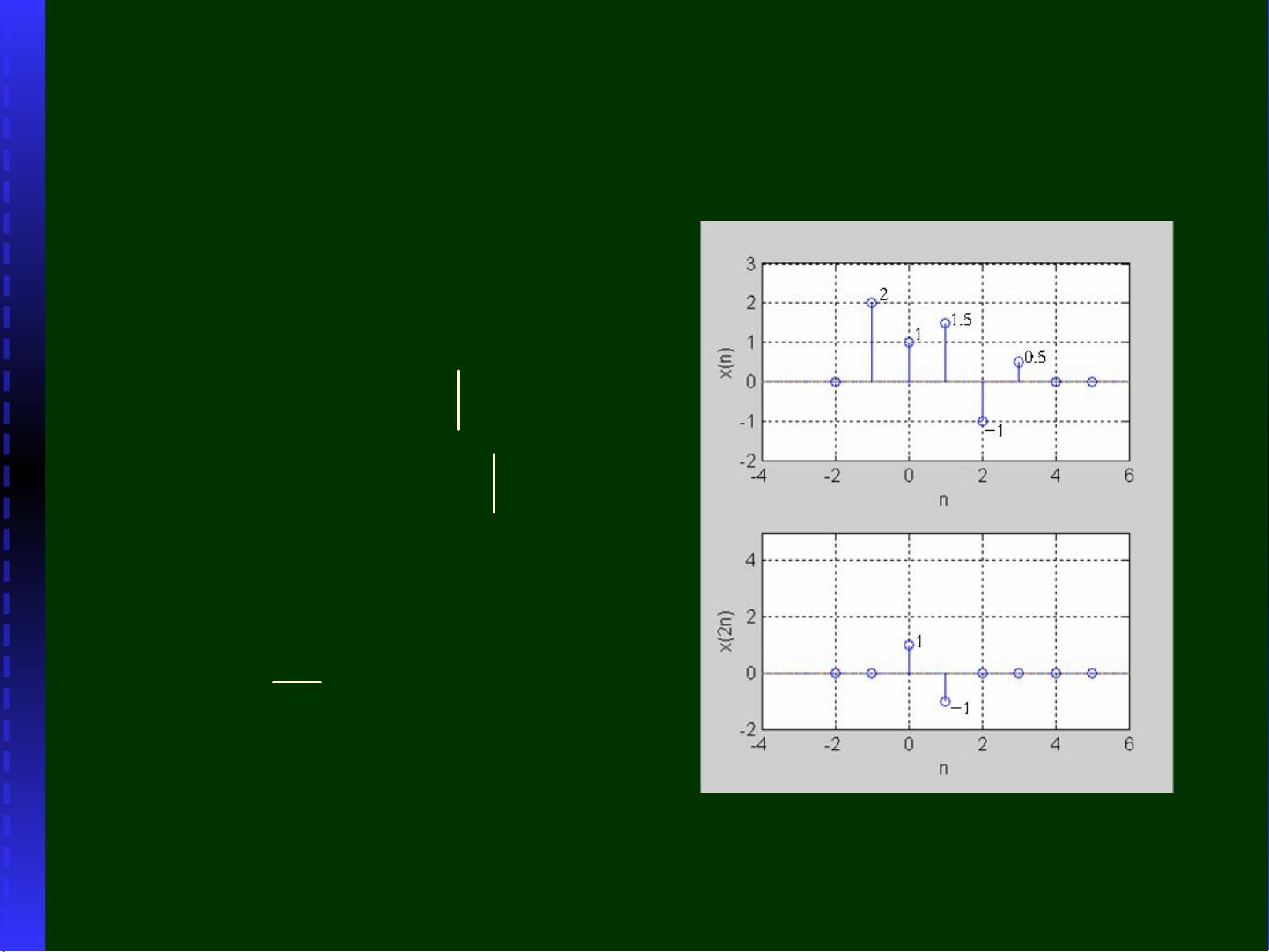 序列的基本运算是本领域的重要部分，包括移位操作，即将序列中的元素按照一定的步长向前或向后移动。除此之外，还有序列的翻转、卷积、傅里叶变换等运算。移位操作是改变序列时间位置的关键，例如，正向移位会将序列的元素向右移动，而负向移位则向左移动。 学习数字信号处理还需掌握线性移不变系统的基本概念。这类系统具有两个关键特性：线性，意味着输入信号的加权组合通过系统后，结果仍然是输入加权组合的相应结果；移不变，表示系统对所有输入信号的响应仅取决于信号本身，而不受输入信号到达系统的时间影响。因果性是指系统的输出只依赖于当前和过去的输入，而与未来的输入无关。稳定性的概念是系统能否在长期运行中保持输出的有限性，这对于实际应用至关重要。 线性移不变系统的稳定性可以通过系统函数（如系统函数H(z)）的极点位置来判断。如果所有极点都位于单位圆内，那么系统是稳定的。另外，常系数线性差分方程是描述这类系统的重要数学工具，可以通过迭代法求解单位抽样响应，这对于分析系统特性非常有用。 此外，连续时间信号的时域抽样是数字信号处理的基石。奈奎斯特抽样定理指出，为了不失真地恢复原始信号，采样频率必须至少是信号最高频率的两倍。抽样后的信号可以通过适当的滤波器和插值过程来重构。 这个资源介绍了数字信号处理的基础，包括序列的定义、表示方法以及与之相关的运算，还涉及了线性移不变系统、稳定性、抽样理论等核心概念。深入理解和掌握这些基础知识是进一步研究数字信号处理和相关应用的前提。