RBF网络：非线性映射与插值应用详解

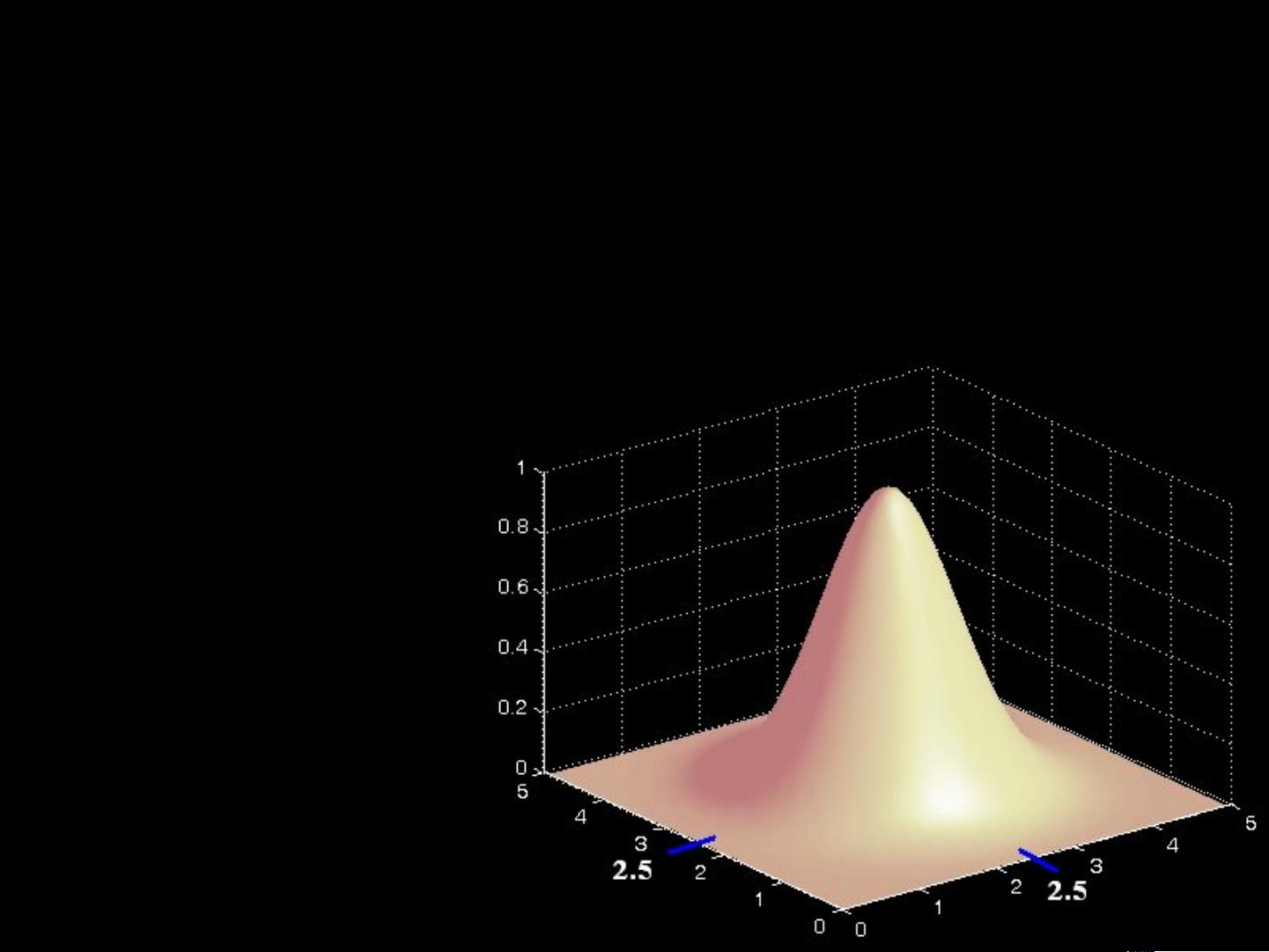
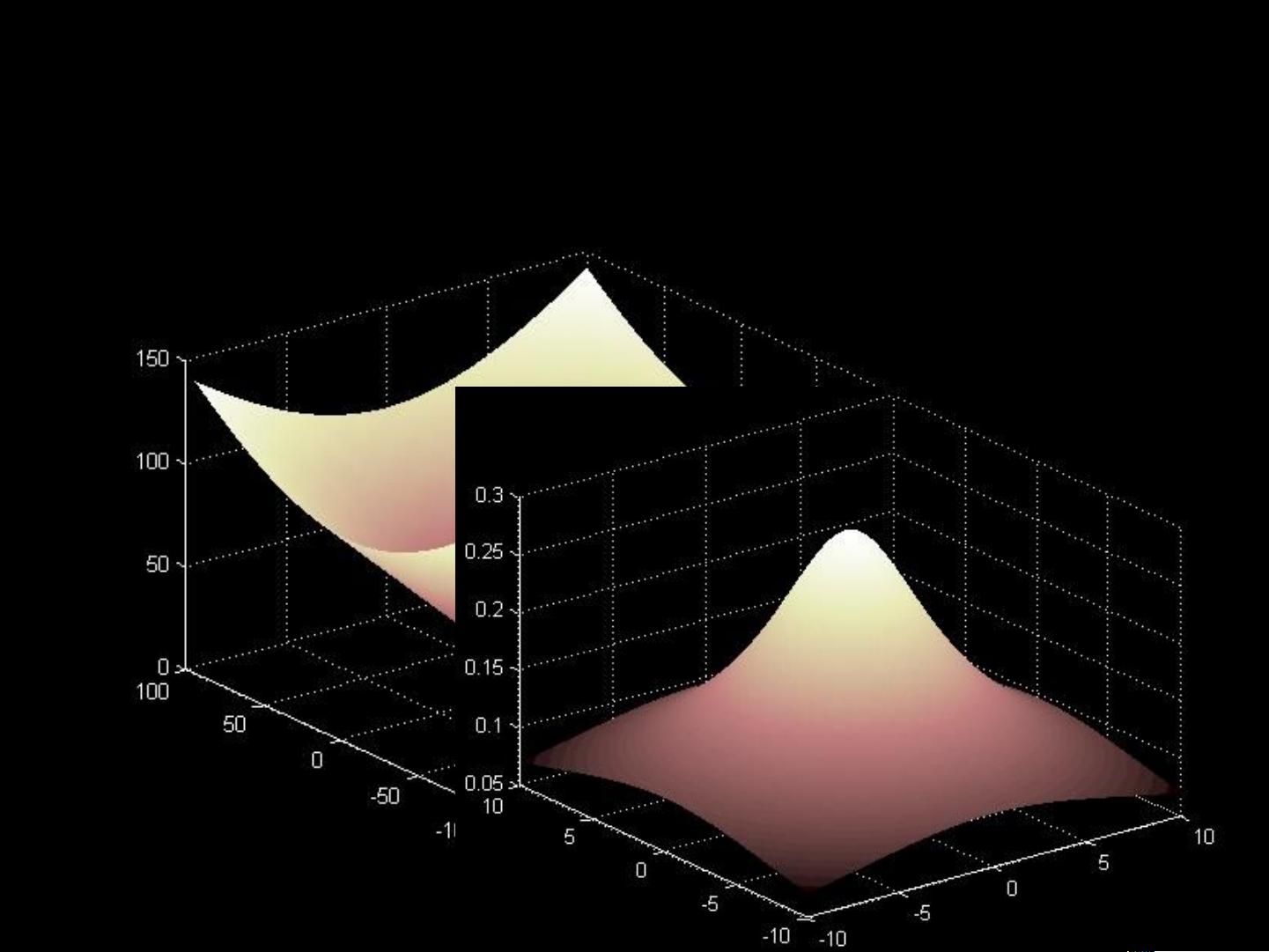
径向基函数网络（RBF Networks）是一种基于径向函数的神经网络模型，主要用于处理复杂的非线性问题，特别是在模式分类和函数逼近领域。它通过将输入特征空间进行非线性变换，使原本难以区分的数据分布变得线性可分，从而实现对复杂问题的有效解决。 1. 解决异或问题: RBF网络被用来解决BP（Backpropagation）算法在处理异或问题时的局限性。BP算法容易陷入局部最优解，因为缺乏全局视角。RBF网络通过非线性映射，将异或问题转换为线性可处理的问题，提高了分类的准确性和全局优化的可能性。 2. 基本思想: RBF网络的核心思想是利用径向基函数作为神经元的激活函数，这些函数的输出只取决于输入数据与中心点的距离。通过这种方式，网络能够在保持简单线性结构的同时，适应高度复杂的输入空间。例如，在异或问题中，通过对输入数据的非线性映射，原本难以用简单线性函数表达的逻辑关系可以被转化为易于分类的形式。 3. Cover模式分类理论: 高维空间中的复杂模式分类问题相较于低维空间通常更容易找到线性可分的解。这是因为随着维度的增加，非线性关系可能会在更高维中变得更容易分离。RBF网络巧妙地利用了这一点，通过构建适当的映射，将问题从原始的非线性问题转移到一个更容易处理的线性问题上。 4. 插值问题: RBF网络也被用于插值任务，如多项式插值，即根据给定的一组输入值和对应输出值来找到一个函数，使其在这些点上的值与目标输出一致。RBF网络的插值函数并非唯一，而且选择的函数复杂度（如多项式的阶数）往往依赖于数据点的数量。例如，当给定5个平面坐标点时，四次多项式可以实现精确的插值，但阶数必须比点数少1。 径向基函数网络是一种强大的工具，通过非线性变换和径向基函数的特性，解决了BP算法在某些复杂问题上的不足，并且在函数逼近和模式分类等领域展现了出色的性能。通过理解其工作原理和适用场景，开发者能够有效地应用RBF网络来处理现实世界的非线性问题。