S分布特性分析：低频优势与多LFM信号处理应用

S分布，也称为S变换，是一种重要的时频分析工具，它在信号处理领域具有独特的特性及广泛应用。本文主要探讨了S分布的数学表达式、原理以及与其它时频分析方法如STFT（短时傅里叶变换）和CWT（连续小波变换）的对比。 S变换的基本原理是通过将STFT中的窗函数转换为高斯窗，其表达式包括一个相位因子，使得S变换能够捕捉信号的局部特征。其数学表达式为\( S(f,t) = \int_{-\infty}^{\infty} x(t) e^{-\pi(f-f_0)^2/(2B^2)}e^{-j2\pi ft} dt \)，其中\( f_0 \)和\( B \)分别代表中心频率和窗函数宽度。其反变换则允许我们从S变换恢复原始信号。 相比于传统的STFT，S变换有其独特之处。在低频部分，S变换提供了更高的分辨率，因为它能够更好地分离低频成分；然而，在高频部分，它的性能不如STFT，这是因为STFT的短时性质使其对高频成分处理更敏感。此外，S变换特别适合检测突发的高频信号，这是STFT在处理这类信号时可能会妥协的地方。 S变换与连续小波变换的关系密切，实际上，S变换可以看作是特定母小波的小波变换加上一个相位因子。这使得S变换能够在保持局部化特性的同时，提供更精确的时间分辨率。 在处理多LFM（线性频率调制）信号时，S变换显示出优势，因为它结合了STFT和CWT的优点，减少了Wigner分布中常见的交叉干扰。Wigner分布对于多LFM信号的处理可能存在限制，但S变换能够更好地应对这种复杂情况。 S变换的应用广泛，特别是在地震检测、生物信号处理和雷达信号处理等领域。例如，文献中提到的自适应时频滤波算法利用S变换实现了对多LFM信号的高效处理，通过GeneralizedS-Transform来消除噪声，显著提高了信号的信噪比。该算法的关键在于识别并剔除噪声，保留信号的时频特征。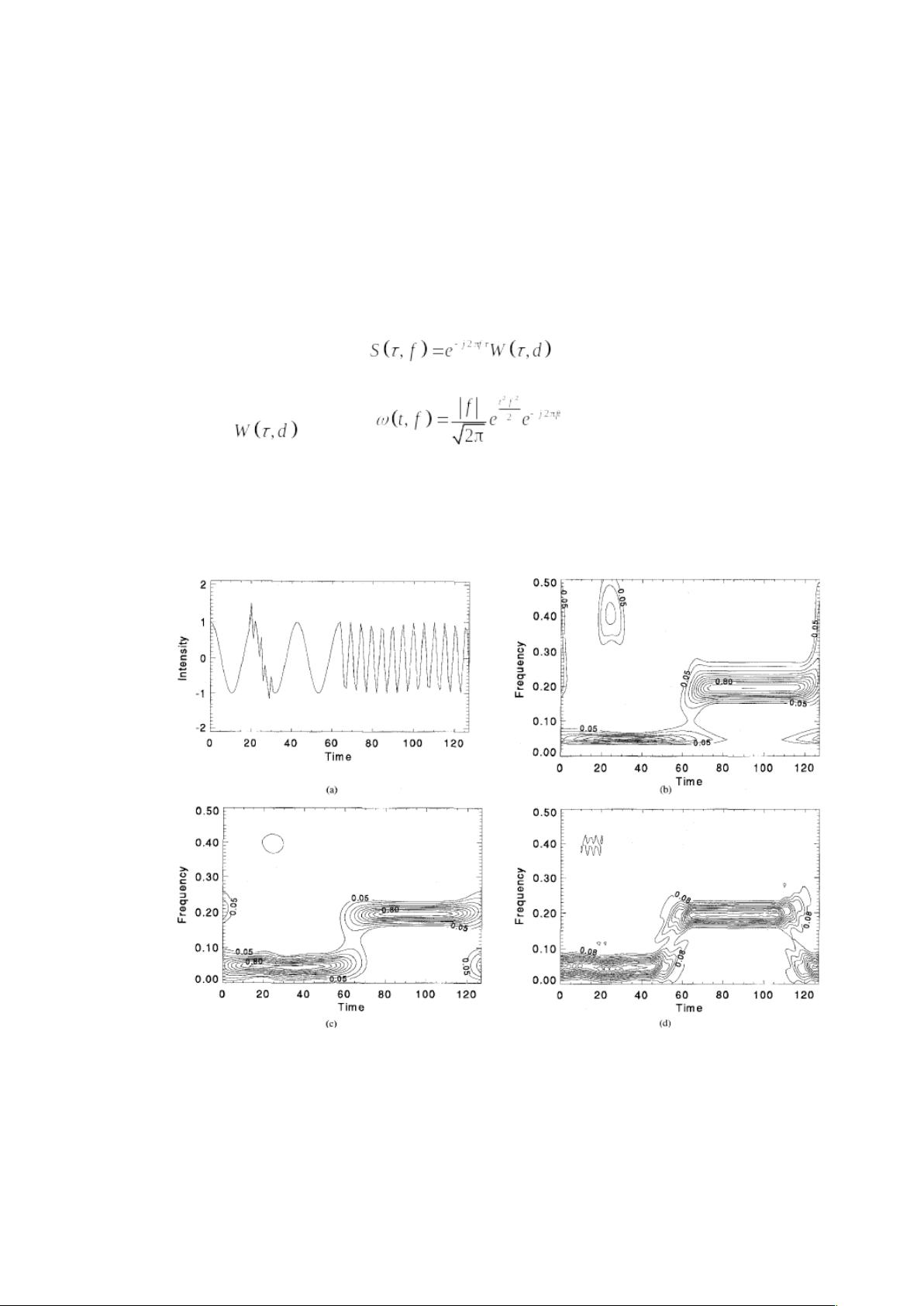 本文作者王雷通过实验验证了这一算法，通过生成两个不同频率和调频的信号s1和s2，以及3dB信噪比的高斯白噪声，对它们的S变换结果进行了分析，展示了S变换在实际信号处理任务中的实用性和有效性。 总结来说，S分布的特性包括其对低频的高分辨率、对突发高频信号的检测能力和在多LFM信号处理中的优势，这些特性使其成为时频分析中不可或缺的一部分。通过深入理解和应用S变换，我们可以有效地解决信号处理中的复杂问题，提高信号的质量和分析精度。