"AIGC与NeurIPS 2020中的DDPM模型解析:从扩散过程到公式预警"
需积分: 14 170 浏览量
更新于2023-12-20
收藏 12.77MB PDF 举报
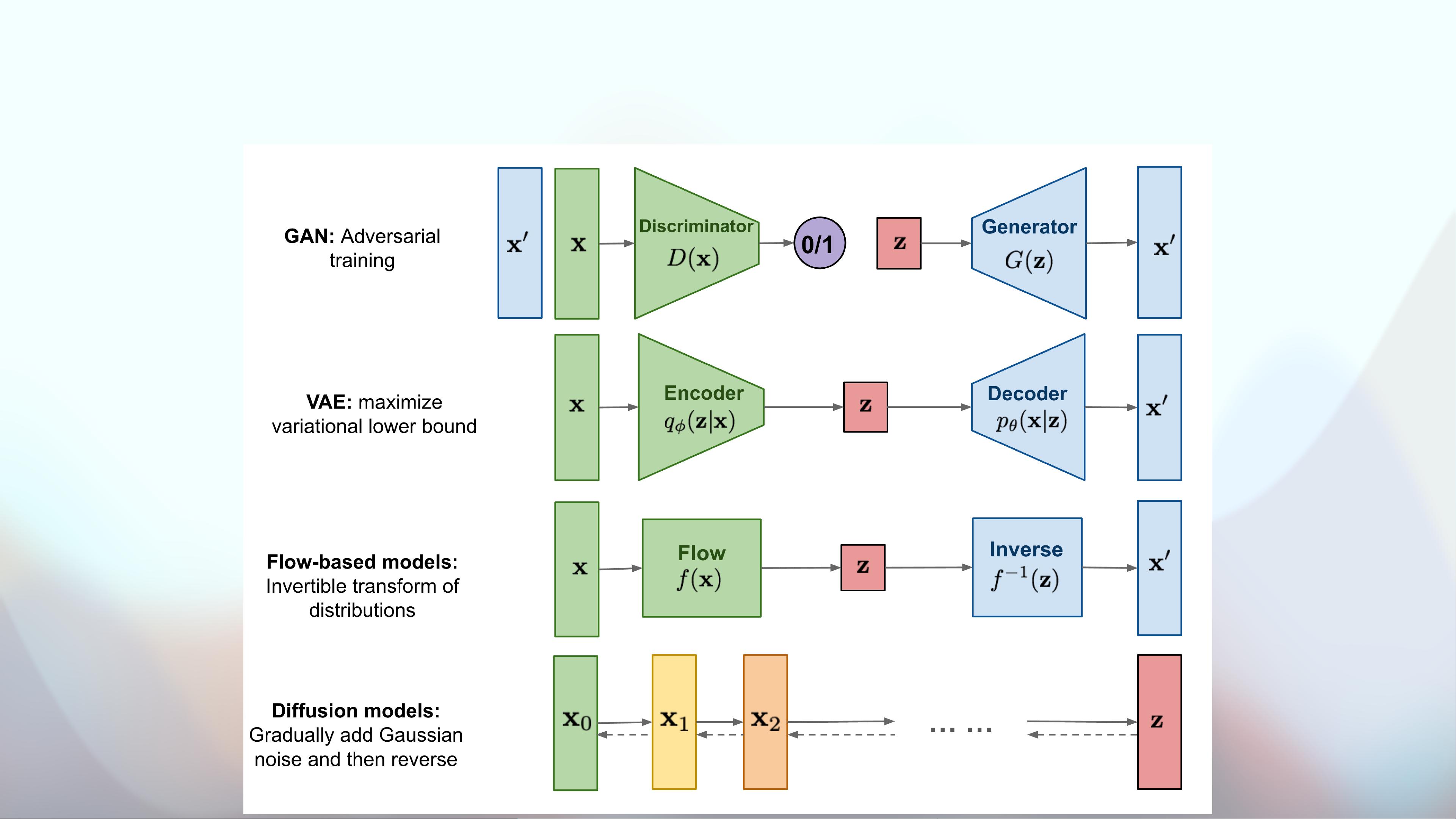
"AIGC与扩散模型(Denoising Diffusion Probabiblistic Model);Denoising Diffusion Probabiblistic Model;Yoghurt.AIGC翌年 来聊聊扩散模型 《Denoising Diffusion Probabiblistic Model》NeurIPS 2020 UC BerkeleyAIGCAI Generated Content⽣成式模型概览DDPM模型图• 前向过程:扩散过程,将真实数据逐步变成噪声• 逆向过程:逆扩散过程,将噪声逐步变成真实数据公式预警预备知识理解扩散过程,你需要了解很多基础知识•:B,C同时发⽣的情况下,A发⽣的概率•:⻉叶斯公式•:均值为 ⽅差为的⾼斯分布表示,概率密度函数p(A|B, C)P(A|B) =P(B|A)P(A)P(B)𝒩(u, σ2)uσ2p(x) =12πσe− 12 ( x − uσ )2前向过程扩散过程:加噪•为原始图像数据,为对原图像进⾏i次加噪(⾼斯噪声)后的结果,当i⾜够⼤时,可以认为噪声淹没了图像,变成纯⾼斯噪声• 等价于•为第i次的扩散率,作为⼀个权值,随着轮次增加逐渐增⼤,可以发现,图像数据和噪声的权值之和不需要为1x0xiz ∼ 𝒩(0,I)xt =1 − βtxt−1 βtzt−1q(xt|xt−1) = 𝒩(xt;1 − ;"可以看出,AIGC通过扩散模型(Denoising Diffusion Probabiblistic Model)的应用,实现了对图像数据的处理和再生。这一模型通过前向过程的扩散过程,将真实数据逐步变成噪声,然后通过逆向过程的逆扩散过程,将噪声逐步变回真实数据,从而实现了对图像数据的去噪和重构。其公式预警预备知识则包括了概率的基本理解、贝叶斯公式以及高斯分布的概率密度函数等内容。对于扩散过程,需要了解多种基础知识,比如在B、C同时发生的情况下,A发生的概率,贝叶斯公式的应用,以及均值为u,方差为σ的高斯分布表示等。在前向过程中,扩散过程通过加噪的方式将原始图像数据逐步淹没在高斯噪声中,最终变成纯高斯噪声。而对应的逆向过程,则是通过一系列的扩散率权值来将噪声逐步变回真实数据。可以看出,AIGC对DDPM模型进行了深入的研究和应用,从根本上实现了图像数据的处理和再生。"
2021-03-19 上传
2023-09-03 上传
2023-11-11 上传
2023-05-18 上传
2023-05-18 上传
2023-05-18 上传
2023-07-24 上传
2022-03-02 上传
ZATuTu丶
- 粉丝: 235
- 资源: 20
最新资源
- C语言数组操作:高度检查器编程实践
- 基于Swift开发的嘉定单车LBS iOS应用项目解析
- 钗头凤声乐表演的二度创作分析报告
- 分布式数据库特训营全套教程资料
- JavaScript开发者Robert Bindar的博客平台
- MATLAB投影寻踪代码教程及文件解压缩指南
- HTML5拖放实现的RPSLS游戏教程
- HT://Dig引擎接口,Ampoliros开源模块应用
- 全面探测服务器性能与PHP环境的iprober PHP探针v0.024
- 新版提醒应用v2:基于MongoDB的数据存储
- 《我的世界》东方大陆1.12.2材质包深度体验
- Hypercore Promisifier: JavaScript中的回调转换为Promise包装器
- 探索开源项目Artifice:Slyme脚本与技巧游戏
- Matlab机器人学习代码解析与笔记分享
- 查尔默斯大学计算物理作业HP2解析
- GitHub问题管理新工具:GIRA-crx插件介绍