坐标转换：从摄氏到华氏与向量变换

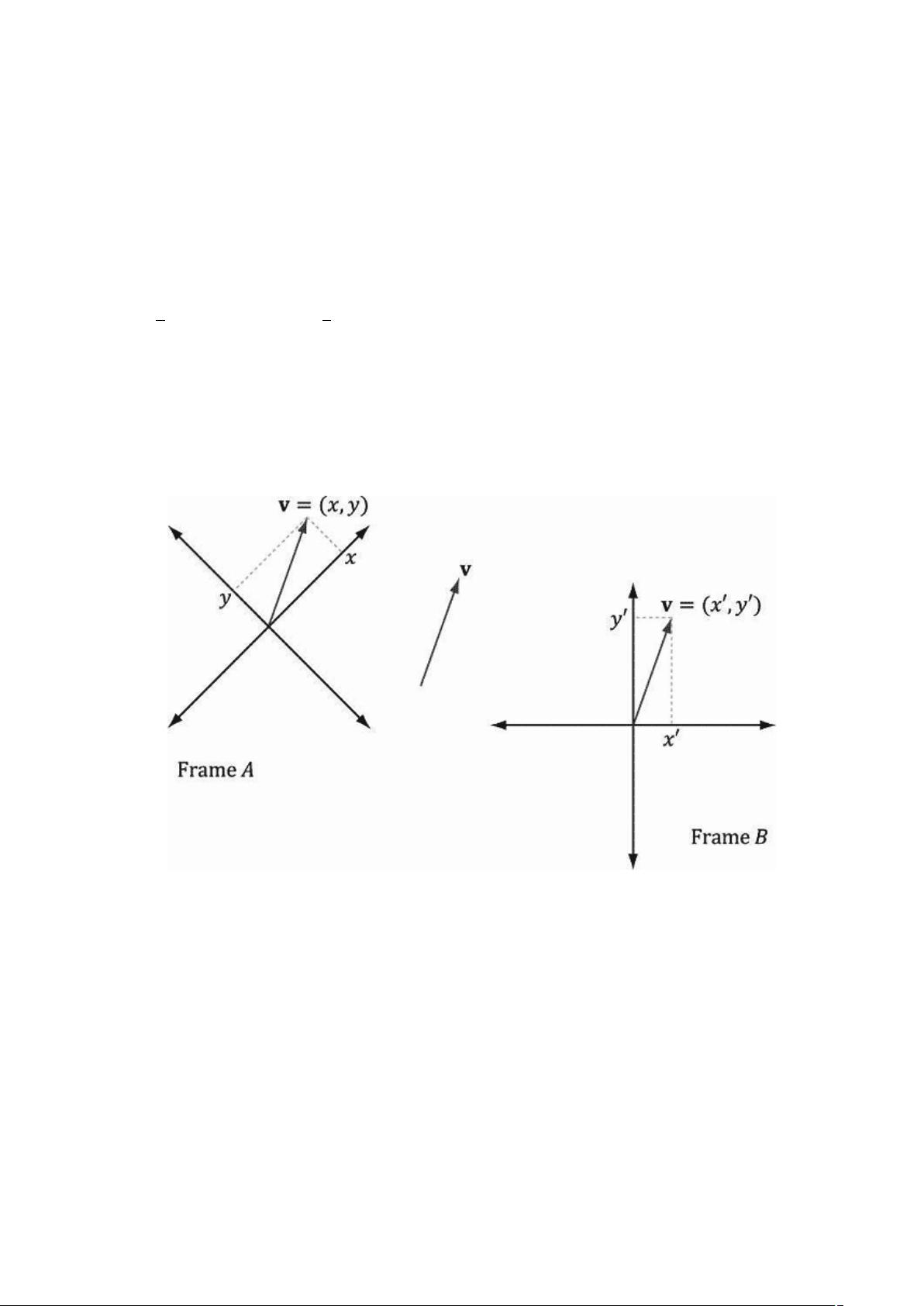
"3.4坐标转换变换1" 在IT领域，尤其是在计算机图形学中，坐标转换变换是一个核心概念。这个变换允许我们在不同的坐标系统之间准确地表示和操作几何数据，如点、向量和物体的位置。当我们从一个坐标系转换到另一个坐标系时，我们并不是改变实际的几何形状，而是改变描述这些形状的数值，因为每个坐标系都有其独立的原点和轴。 在3.4.1小节中，向量的坐标转换被详细讨论。考虑两个参考系A和B，以及一个位于这两个参考系中的向量p。向量p在参考系A中的坐标表示为pA=(x,y)，而目标是找到它在参考系B中的坐标pB=(xʹ,yʹ)。这里的关键在于理解，尽管向量p的物理位置没有变，但其在不同坐标系下的坐标表示会变化。 向量p可以表示为它的基向量u和v的线性组合，即p=xu+yv。这里的u和v是单位向量，与参考系A的x轴和y轴平行。为了在参考系B中表示向量p，我们需要知道u和v在新坐标系B中的坐标，即uB=(ux,uy)和vB=(vx,vy)。因此，向量p在参考系B中的坐标可以通过以下方式计算： pB = xuB + yvB 对于三维情况，当pA=(x,y,z)时，转换过程类似，只是增加了一个z坐标： pB = xuB + yvB + wzB 这里的w对应于参考系A中向量p的z轴分量，而uB、vB和wB分别是u、v和w在参考系B中的坐标表示。 在3D计算机图形学中，坐标转换变换的应用非常广泛，例如在场景中放置对象、进行摄像机视图变换、应用光照效果，甚至是模拟物理运动。这些变换通常包括平移、旋转和缩放，它们通过矩阵运算来实现，使得计算更加简洁和高效。 理解并掌握坐标转换变换对于开发3D应用程序至关重要，它能够帮助我们在不同的坐标系统间有效地表示和操纵图形元素，确保图形的一致性和准确性。无论是2D游戏还是复杂的虚拟现实环境，良好的坐标转换能力都是开发者必备的技术之一。