时间序列加性离群点检测：基于残差统计的新方法

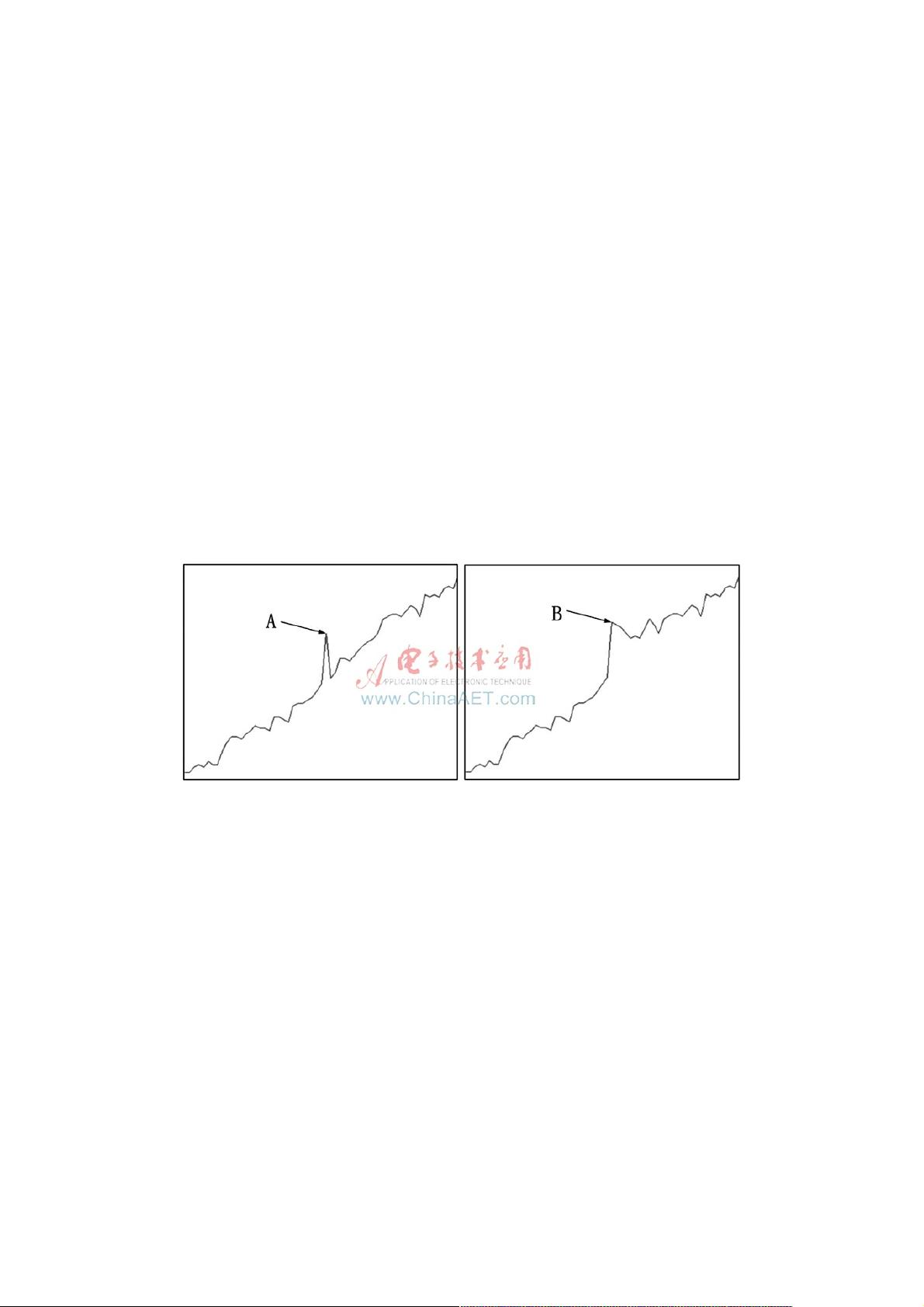
"该文研究了一种基于残差统计的时间序列加性离群点检测算法，利用AR模型进行前向和后向拟合，通过数据相对变化率判别法减少离群点对拟合的影响，并基于高斯分布的假设检验确定离群点。这种方法在仿真中表现出高准确性，特别关注时间序列中的加性离群点检测。" 在时间序列分析中，离群点的检测是一项关键任务，因为它们可能掩盖真实模式或导致错误的分析结果。离群点可以分为多种类型，如孤立离群点和成片离群点，以及加性、更新、水平移位和暂时变更离群点。本文主要关注加性离群点，这类离群点直接改变了时间序列的平均值，而不会影响序列的结构。 传统的离群点检测方法包括统计、距离、密度和偏离方法。然而，针对有序的时间序列数据，需要更特定的策略。统计诊断和贝叶斯方法、遗传算法、神经网络和小波分析是常见的技术。文献中提到的粗糙集理论、多变量时间序列相似度矩阵和数据相对变化率等方法也展示了离群点检测的多样性。 本文提出了一种基于残差统计的加性离群点检测算法。首先，利用自回归(AR)模型对时间序列进行前向和后向拟合，以捕获序列的动态行为。AR模型是一种常用的线性预测模型，能够捕捉序列内的依赖关系。然后，通过数据相对变化率判别法，评估每个数据点与前后时刻的变化，这种方法有助于减弱离群点对拟合过程的干扰。最后，基于假设检验的原理，利用高斯分布的统计检验来分析残差。如果残差的统计特性显著偏离高斯分布，那么这可能表明存在离群点。 通过这样的流程，算法能够更准确地识别出加性离群点，尤其是在考虑时间序列趋势和其他复杂变化的情况下。在仿真实验中，该方法表现出了高精度，证明了其在检测加性离群点方面的有效性。这种方法的优势在于它能够适应时间序列的内在结构，并且通过统计分析减少了误判的可能性。 这种基于残差统计的加性离群点检测算法为时间序列分析提供了一个新的工具，特别是在监测和排除可能影响数据分析的异常值时。这种方法对于各种应用领域，如金融、环境监测、工业生产等，都有重要的实用价值，因为它可以帮助确保数据分析的准确性和可靠性。