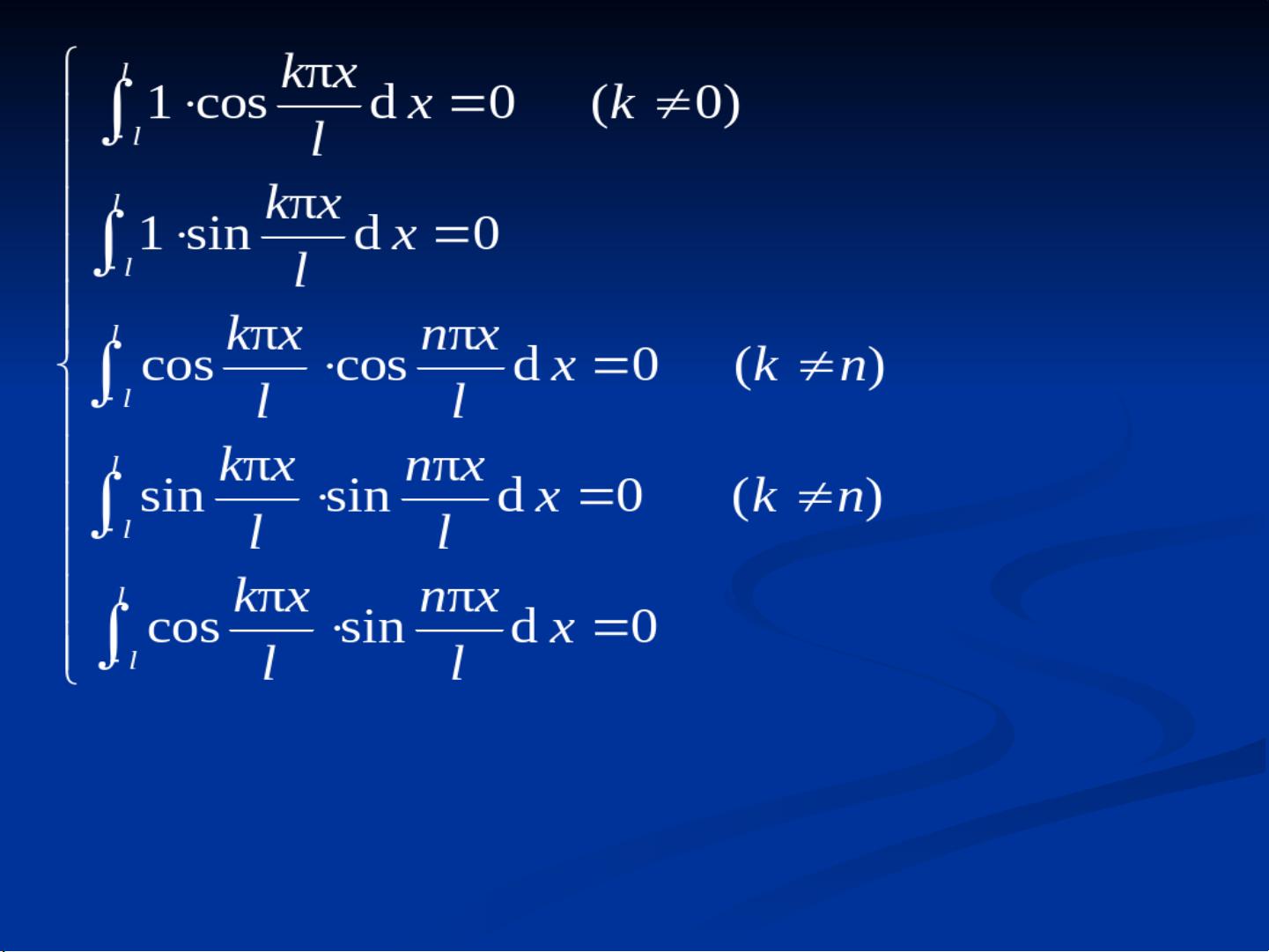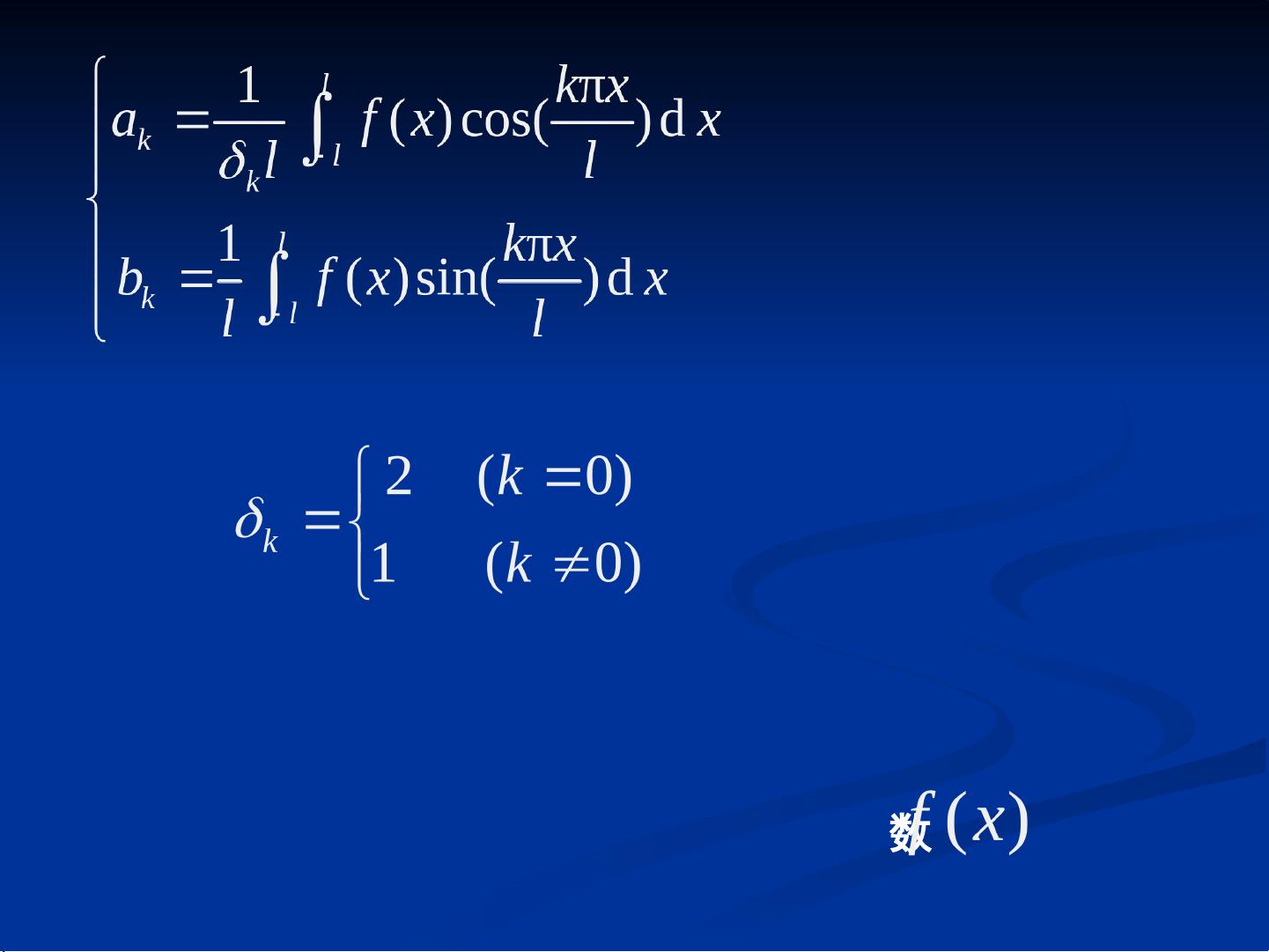傅里叶变换解析与应用

"傅里叶变换是数学中一种重要的积分变换方法，用于简化复杂运算，尤其在解决微分方程和信号处理等领域有着广泛应用。它将一个函数转换为其频域表示，通过特定的核函数（如指数函数）进行积分。傅里叶变换的基本形式涉及到将时间域的函数转化为频率域的函数，而逆变换则反之。本文档详细讲解了傅里叶变换的原理、方法及其在工程中的应用。" 傅里叶变换是一种在各个科学和技术领域广泛使用的数学工具，它能够将复杂的时域信号转换到频域进行分析。这个变换过程通过一个特定的积分操作完成，将原本难以处理的微分或积分运算转化为简单的代数操作。这极大地简化了解决问题的难度，特别是在处理涉及微分方程的问题时。 在傅里叶变换中，给定一个函数f(t)，它可以通过一个积分变换转化为另一个函数F(ω)，这个过程可以表示为： \[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j\omega t} dt \] 这里的\( e^{-j\omega t} \)是傅里叶变换的核函数，\( j \)是虚数单位，\( \omega \)是频率变量。函数F(ω)被称为f(t)的傅里叶变换，而f(t)则是F(ω)的傅里叶逆变换。 傅里叶变换的主要应用包括： 1. **微分方程的求解**：傅里叶变换可以把微分方程转化为代数方程，从而简化求解过程。在频域中找到的解，再通过逆变换可以得到原问题的时域解。 2. **信号分析**：在电子工程和通信领域，傅里叶变换用于分析信号的频率成分，帮助理解信号的频谱结构。 3. **图像处理**：在图像处理中，傅里叶变换用于提取图像的频域特征，例如进行滤波和压缩。 4. **物理问题的解决**：在量子力学和热力学等领域，傅里叶变换被用来处理波动现象和能量分布。 5. **数据压缩**：在信息科技中，通过傅里叶变换可以有效地进行数据编码和压缩，例如JPEG图片压缩标准就利用了离散傅里叶变换。 6. **频谱分析**：在音频处理中，傅里叶变换用于分析声音信号的频率组成，帮助我们理解和修改音乐或语音信号。 傅里叶变换的另一个变种是拉普拉斯变换，其核函数为\( e^{-pt} \)，p是复数参数。拉普拉斯变换主要在稳定性分析和控制系统设计中发挥作用，因为它能够处理随时间增长趋于稳定的系统。 傅里叶变换是一个强大的数学工具，它揭示了函数在不同域之间的内在联系，为解决各种实际问题提供了理论基础和计算手段。无论是在理论研究还是工程实践，傅里叶变换都扮演着不可或缺的角色。