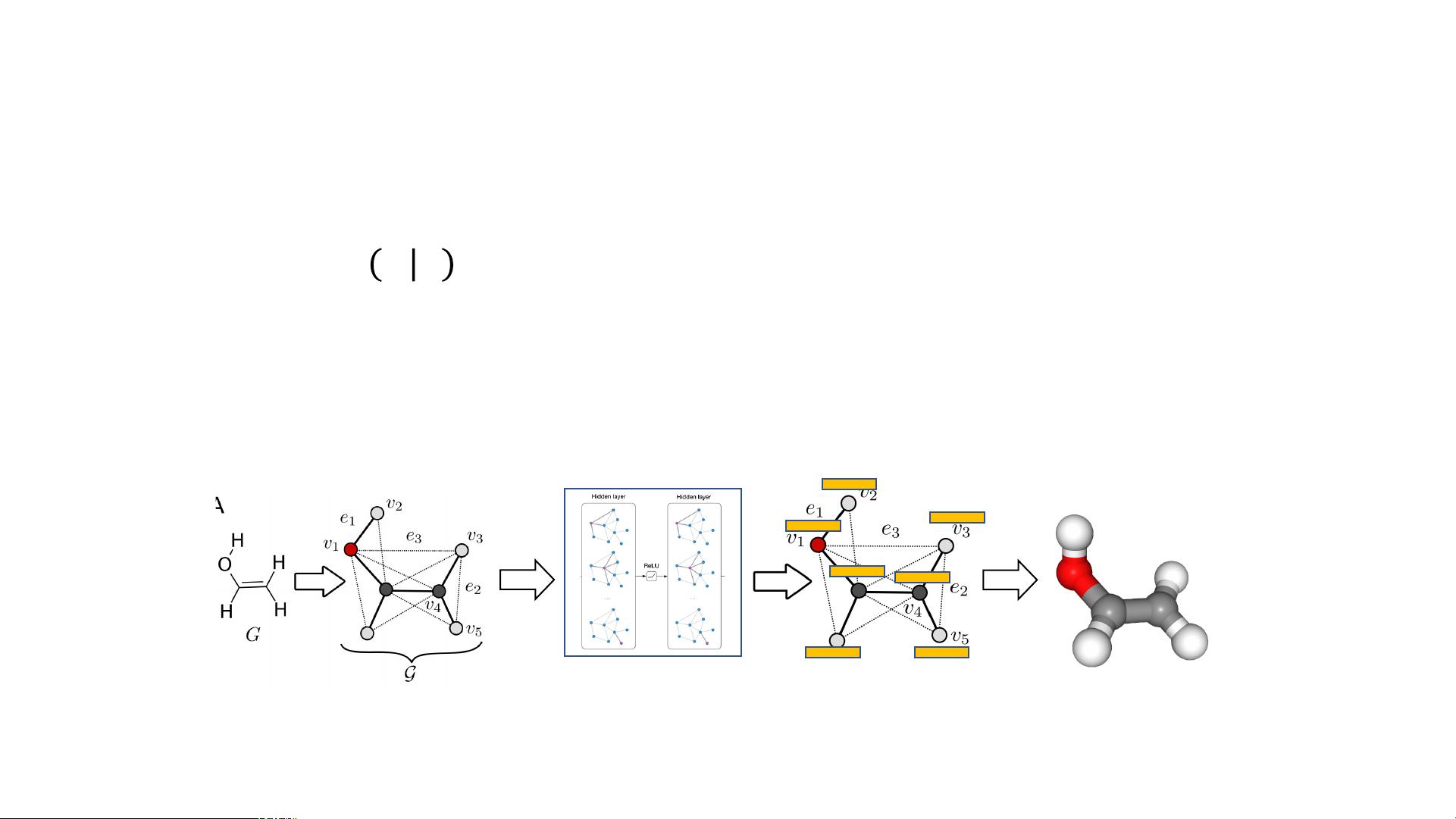
Machine Learning-based Approaches
• Train a model to predict molecular conformations 𝑹 given the molecular graph 𝒢,
i.e., modeling p 𝑹 𝒢
• Conditional Variational Graph Autoencoder (CVGAE) (Mansimov et al. 2019)
• VA E framework: encoder 𝑞(𝑧 ∣ 𝒢, 𝑹), decoder 𝑝(𝑹 ∣ 𝑧, 𝒢)
• Encoder: Learning atomic latent representations with graph neural networks
• Decoder: Predicting atom coordinates based on atom representations
≈
Graph Neural
Networks
Graph Neural Networks
≈
Node/Atom RepresentationsAugmented Molecular Graph Conformations
6
Under review as a conference paper at ICLR 2021
G
<latexit sha1_base64="vIs0DtZMVgyrXYZyWvMVVQo2iJ8=">AAAB8nicbVDLSgMxFM3UV62vqks3wSK4kDIjBXVXcKHLCvYB06Fk0kwbmkmG5I5Qhn6GGxeKuPVr3Pk3ZtpZaOuBwOGce8m5J0wEN+C6305pbX1jc6u8XdnZ3ds/qB4edYxKNWVtqoTSvZAYJrhkbeAgWC/RjMShYN1wcpv73SemDVfyEaYJC2IykjzilICV/H5MYEyJyO5mg2rNrbtz4FXiFaSGCrQG1a/+UNE0ZhKoIMb4nptAkBENnAo2q/RTwxJCJ2TEfEsliZkJsnnkGT6zyhBHStsnAc/V3xsZiY2ZxqGdzCOaZS8X//P8FKLrIOMySYFJuvgoSgUGhfP78ZBrRkFMLSFUc5sV0zHRhIJtqWJL8JZPXiWdy7rXqN88NGrNi6KOMjpBp+gceegKNdE9aqE2okihZ/SK3hxwXpx352MxWnKKnWP0B87nD3aukVM=</latexit>
N(0, I)
<latexit sha1_base64="ZURxyFRkumcoZhtLB9tuZDzUxpQ=">AAACFHicbVDLSgMxFM34rPU16rKbYBEqSJmRgroruNGNVLAP6JSSSTNtaJIZkoxQhln4E/6CW927E7fu3folZtpZ2NYDIYdz7uXee/yIUaUd59taWV1b39gsbBW3d3b39u2Dw5YKY4lJE4cslB0fKcKoIE1NNSOdSBLEfUba/vg689uPRCoaigc9iUiPo6GgAcVIG6lvlzyO9AgjltylFc/niZOewey/TU/7dtmpOlPAZeLmpAxyNPr2jzcIccyJ0JghpbquE+legqSmmJG06MWKRAiP0ZB0DRWIE9VLpkek8MQoAxiE0jyh4VT925EgrtSE+6YyW1ktepn4n9eNdXDZS6iIYk0Eng0KYgZ1CLNE4IBKgjWbGIKwpGZXiEdIIqxNbnNTfJ4WTSjuYgTLpHVedWvVq/tauV7J4ymAEjgGFeCCC1AHN6ABmgCDJ/ACXsGb9Wy9Wx/W56x0xcp7jsAcrK9foQCeKQ==</latexit>
d(t
0
)
<latexit sha1_base64="S5vzONPPGcE2Bnxqdal57hBhNUE=">AAACAnicbVDLSsNAFJ3UV62vqks3g0Wom5JIQd0V3LisYB+QhjKZTNqh8wgzE6GE7PwFt7p3J279Ebd+idM2C9t64MLhnHu5954wYVQb1/12ShubW9s75d3K3v7B4VH1+KSrZaow6WDJpOqHSBNGBekYahjpJ4ogHjLSCyd3M7/3RJSmUjyaaUICjkaCxhQjYyV/EPIsyutm6F4OqzW34c4B14lXkBoo0B5WfwaRxCknwmCGtPY9NzFBhpShmJG8Mkg1SRCeoBHxLRWIEx1k85NzeGGVCMZS2RIGztW/ExniWk95aDs5MmO96s3E/zw/NfFNkFGRpIYIvFgUpwwaCWf/w4gqgg2bWoKwovZWiMdIIWxsSktbQp5XbCjeagTrpHvV8JqN24dmrVUv4imDM3AO6sAD16AF7kEbdAAGEryAV/DmPDvvzofzuWgtOcXMKViC8/UL8JyXWw==</latexit>
F
✓
<latexit sha1_base64="F31lh5CKHaiA3aXYW2ZI+Y7ONAQ=">AAAB/3icbVA9SwNBEJ2LXzF+RS1tFoNgIeFOAmoXEMQygvmA5Ah7m71kye7dsTsnhJDCv2CrvZ3Y+lNs/SVukitM4oOBx3szzMwLEikMuu63k1tb39jcym8Xdnb39g+Kh0cNE6ea8TqLZaxbATVciojXUaDkrURzqgLJm8Hwduo3n7g2Io4ecZRwX9F+JELBKFqpddft4IAj7RZLbtmdgawSLyMlyFDrFn86vZilikfIJDWm7bkJ+mOqUTDJJ4VOanhC2ZD2edvSiCpu/PHs3gk5s0qPhLG2FSGZqX8nxlQZM1KB7VQUB2bZm4r/ee0Uw2t/LKIkRR6x+aIwlQRjMn2e9ITmDOXIEsq0sLcSNqCaMrQRLWwJ1KRgQ/GWI1gljcuyVynfPFRK1YssnjycwCmcgwdXUIV7qEEdGEh4gVd4c56dd+fD+Zy35pxs5hgW4Hz9AkIZln0=</latexit>
d(t
1
)
<latexit sha1_base64="3uFAD5t20r5hkITaCaR1FRhMgvY=">AAACAnicbVDLSsNAFJ3UV62vqks3g0Wom5JIQd0V3LisYB+QhjKZTNqh8wgzE6GE7PwFt7p3J279Ebd+idM2C9t64MLhnHu5954wYVQb1/12ShubW9s75d3K3v7B4VH1+KSrZaow6WDJpOqHSBNGBekYahjpJ4ogHjLSCyd3M7/3RJSmUjyaaUICjkaCxhQjYyV/EPIsyutm6F0OqzW34c4B14lXkBoo0B5WfwaRxCknwmCGtPY9NzFBhpShmJG8Mkg1SRCeoBHxLRWIEx1k85NzeGGVCMZS2RIGztW/ExniWk95aDs5MmO96s3E/zw/NfFNkFGRpIYIvFgUpwwaCWf/w4gqgg2bWoKwovZWiMdIIWxsSktbQp5XbCjeagTrpHvV8JqN24dmrVUv4imDM3AO6sAD16AF7kEbdAAGEryAV/DmPDvvzofzuWgtOcXMKViC8/UL8jGXXA==</latexit>
p
✓
(d|G)
<latexit sha1_base64="BSPQokcnd67Ox4bSGWxni9WSepw=">AAACF3icbVBNS8NAEN3Ur1q/qh4FWSxCBSmJFNRbwYMeK9gPaErZbDft0t0k7E6EEnPzT/gXvOrdm3j16NVf4rbNwVYfDDzem2FmnhcJrsG2v6zc0vLK6lp+vbCxubW9U9zda+owVpQ1aChC1faIZoIHrAEcBGtHihHpCdbyRlcTv3XPlOZhcAfjiHUlGQTc55SAkXrFw6jnwpABKbueTPopfsCuJDCkRCTX6UmvWLIr9hT4L3EyUkIZ6r3it9sPaSxZAFQQrTuOHUE3IQo4FSwtuLFmEaEjMmAdQwMime4m0z9SfGyUPvZDZSoAPFV/TyREaj2Wnumc3KgXvYn4n9eJwb/oJjyIYmABnS3yY4EhxJNQcJ8rRkGMDSFUcXMrpkOiCAUT3dwWT6YFE4qzGMFf0jyrONXK5W21VDvN4smjA3SEyshB56iGblAdNRBFj+gZvaBX68l6s96tj1lrzspm9tEcrM8feuyfvQ==</latexit>
p(R|d , G)
<latexit sha1_base64="dhDz+mg0jfbxnERYd0jVT19v2HI=">AAACGHicbZDLSsNAFIYnXmu9RV26cLAIFUpJpKDuCi50WcVeoAllMpm2Q2eSMDMRSszSl/AV3Orenbh159YncdJmYVt/GPj4zzmcM78XMSqVZX0bS8srq2vrhY3i5tb2zq65t9+SYSwwaeKQhaLjIUkYDUhTUcVIJxIEcY+Rtje6yurtByIkDYN7NY6Iy9EgoH2KkdJWzzyKyo7Hk7sUPsIM/LQCHY7UECOWXKenPbNkVa2J4CLYOZRArkbP/HH8EMecBAozJGXXtiLlJkgoihlJi04sSYTwCA1IV2OAOJFuMvlICk+048N+KPQLFJy4fycSxKUcc093ZjfK+Vpm/lfrxqp/4SY0iGJFAjxd1I8ZVCHMUoE+FQQrNtaAsKD6VoiHSCCsdHYzWzyeFnUo9nwEi9A6q9q16uVtrVSv5PEUwCE4BmVgg3NQBzegAZoAgyfwAl7Bm/FsvBsfxue0dcnIZw7AjIyvX4fin7c=</latexit>
R
<latexit sha1_base64="gQ1W5BUBQuSs4llOR92XD3cLttw=">AAAB/XicbVA9SwNBEJ2LXzF+RS1tFoOQKtyJoHYBG8so5gOSI+xt9pI1u3vH7p4QjsO/YKu9ndj6W2z9JW6SK0zig4HHezPMzAtizrRx3W+nsLa+sblV3C7t7O7tH5QPj1o6ShShTRLxSHUCrClnkjYNM5x2YkWxCDhtB+Obqd9+okqzSD6YSUx9gYeShYxgY6VWLxDpfdYvV9yaOwNaJV5OKpCj0S//9AYRSQSVhnCsdddzY+OnWBlGOM1KvUTTGJMxHtKupRILqv10dm2GzqwyQGGkbEmDZurfiRQLrScisJ0Cm5Fe9qbif143MeGVnzIZJ4ZKMl8UJhyZCE1fRwOmKDF8YgkmitlbERlhhYmxAS1sCURWsqF4yxGsktZ5zbuoXd9dVOrVPJ4inMApVMGDS6jDLTSgCQQe4QVe4c15dt6dD+dz3lpw8pljWIDz9QvyzpXD</latexit>
p(R|d, G)
<latexit sha1_base64="OpcR7prbb0BxuXfNQa1FkN+WMYo=">AAACGHicbZDLSsNAFIYn9VbrLerShYNFqCAlkYK6K7jQZRV7gSaUyWTaDp1JwsxEKDFLX8JXcKt7d+LWnVufxEmbhW39YeDjP+dwzvxexKhUlvVtFJaWV1bXiuuljc2t7R1zd68lw1hg0sQhC0XHQ5IwGpCmooqRTiQI4h4jbW90ldXbD0RIGgb3ahwRl6NBQPsUI6WtnnkYVRyPJ3cpfIQZ+OkpdDhSQ4xYcp2e9MyyVbUmgotg51AGuRo988fxQxxzEijMkJRd24qUmyChKGYkLTmxJBHCIzQgXY0B4kS6yeQjKTzWjg/7odAvUHDi/p1IEJdyzD3dmd0o52uZ+V+tG6v+hZvQIIoVCfB0UT9mUIUwSwX6VBCs2FgDwoLqWyEeIoGw0tnNbPF4WtKh2PMRLELrrGrXqpe3tXK9ksdTBAfgCFSADc5BHdyABmgCDJ7AC3gFb8az8W58GJ/T1oKRz+yDGRlfv4aun7M=</latexit>
E
<latexit sha1_base64="lhItiocMBRqGObaIUKv7lTDqZ9g=">AAAB/XicbVBNSwMxEJ2tX7V+VT16CRbBg5RdKVRvBRE8VrAf0C4lm2bb2CS7JFmhLMW/4FXv3sSrv8Wrv8S03YNtfTDweG+GmXlBzJk2rvvt5NbWNza38tuFnd29/YPi4VFTR4kitEEiHql2gDXlTNKGYYbTdqwoFgGnrWB0M/VbT1RpFskHM46pL/BAspARbKzUvO114yHrFUtu2Z0BrRIvIyXIUO8Vf7r9iCSCSkM41rrjubHxU6wMI5xOCt1E0xiTER7QjqUSC6r9dHbtBJ1ZpY/CSNmSBs3UvxMpFlqPRWA7BTZDvexNxf+8TmLCKz9lMk4MlWS+KEw4MhGavo76TFFi+NgSTBSztyIyxAoTYwNa2BKIScGG4i1HsEqal2WvUr6+r5RqF1k8eTiBUzgHD6pQgzuoQwMIPMILvMKb8+y8Ox/O57w152Qzx7AA5+sXoUCVkw==</latexit>
E
(R, G)
<latexit sha1_base64="8NEpmi0zn1Gl+TfONZYwYrCHrJU=">AAACFHicbVDLSsNAFJ34rPUVddnNYBEqlJJIQd0VRHRZxT6gCWUynbRDZ5IwMxFKyMKf8Bfc6t6duHXv1i9x0mZhWw9cOJxzL/fe40WMSmVZ38bK6tr6xmZhq7i9s7u3bx4ctmUYC0xaOGSh6HpIEkYD0lJUMdKNBEHcY6Tjja8yv/NIhKRh8KAmEXE5GgbUpxgpLfXN0nXfiUa04ng8uU+r0OFIjTBiyU162jfLVs2aAi4TOydlkKPZN3+cQYhjTgKFGZKyZ1uRchMkFMWMpEUnliRCeIyGpKdpgDiRbjJ9IoUnWhlAPxS6AgWn6t+JBHEpJ9zTndmNctHLxP+8Xqz8CzehQRQrEuDZIj9mUIUwSwQOqCBYsYkmCAuqb4V4hATCSuc2t8XjaVGHYi9GsEzaZzW7Xru8q5cb1TyeAiiBY1ABNjgHDXALmqAFMHgCL+AVvBnPxrvxYXzOWleMfOYIzMH4+gWBw54d</latexit>
R
<latexit sha1_base64="gQ1W5BUBQuSs4llOR92XD3cLttw=">AAAB/XicbVA9SwNBEJ2LXzF+RS1tFoOQKtyJoHYBG8so5gOSI+xt9pI1u3vH7p4QjsO/YKu9ndj6W2z9JW6SK0zig4HHezPMzAtizrRx3W+nsLa+sblV3C7t7O7tH5QPj1o6ShShTRLxSHUCrClnkjYNM5x2YkWxCDhtB+Obqd9+okqzSD6YSUx9gYeShYxgY6VWLxDpfdYvV9yaOwNaJV5OKpCj0S//9AYRSQSVhnCsdddzY+OnWBlGOM1KvUTTGJMxHtKupRILqv10dm2GzqwyQGGkbEmDZurfiRQLrScisJ0Cm5Fe9qbif143MeGVnzIZJ4ZKMl8UJhyZCE1fRwOmKDF8YgkmitlbERlhhYmxAS1sCURWsqF4yxGsktZ5zbuoXd9dVOrVPJ4inMApVMGDS6jDLTSgCQQe4QVe4c15dt6dD+dz3lpw8pljWIDz9QvyzpXD</latexit>
p
<latexit sha1_base64="ORiRlP3d8Ck3qImxG8IgZjn4WBQ=">AAAB+HicbVA9SwNBEJ2LXzF+RS1tFoNgIeFOAmoXsLFMwHxAcoS9zSRZsnt37O4J8cgvsNXeTmz9N7b+EjfJFSbxwcDjvRlm5gWx4Nq47reT29jc2t7J7xb29g8Oj4rHJ00dJYphg0UiUu2AahQ8xIbhRmA7VkhlILAVjO9nfusJleZR+GgmMfqSDkM+4IwaK9XjXrHklt05yDrxMlKCDLVe8afbj1giMTRMUK07nhsbP6XKcCZwWugmGmPKxnSIHUtDKlH76fzQKbmwSp8MImUrNGSu/p1IqdR6IgPbKakZ6VVvJv7ndRIzuPVTHsaJwZAtFg0SQUxEZl+TPlfIjJhYQpni9lbCRlRRZmw2S1sCOS3YULzVCNZJ87rsVcp39UqpepXFk4czOIdL8OAGqvAANWgAA4QXeIU359l5dz6cz0VrzslmTmEJztcvBTaTkA==</latexit>
Gradient
Descent
MCMC
Predict distances for
the input graph.
Search 3D coordinates
given the distances.
Input Graph
Further optimize the
generated structures.
Flow
Dynamics
Figure 1: Illustration of the proposed framework. Given the molecular graph, we 1) first draw latent variables
from a Gaussian prior, and transform them to the desired distance matrix through the Conditional Graph Con-
tinuous Flow (CGCF); 2) search the possible 3D coordinates according to the generated distances and 3) further
optimize the generated conformation via a MCMC procedure with the Energy-based Tilting Model (ETM).
where p
✓
(d|G) models the distribution of inter-atomic distances given the graph G and p(R|d, G)
models the distribution of conformations given the distances d. In particular, the conditional gener-
ative model p
✓
(d|G) is parameterized as a conditional graph continuous flow, which can be seen as
a continuous dynamics system to transform the random initial noise to meaningful distances. This
flow model enables us to capture the long-range dependencies between atoms in the hidden space
during the dynamic steps.
Though CGCF can capture the dependency between atoms in the hidden space, the distances of
different edges are still independently updated in the transformations, which limits the capacity of
modeling the dependency between atoms in the sampling process. Therefore we further propose to
correct p
✓
(R|G) with an energy-based tilting term E
(R, G):
p
✓,
(R|G) / p
✓
(R|G) · exp( E
(R, G)). (5)
The tilting term is directly defined on the joint distribution of R and G, which explicitly captures the
long-range interaction directly in observation space. The tilted distribution p
✓,
(R|G) can be used
to provide refinement or optimization for the conformations generated from p
✓
(R|G). This energy
function is also designed to be invariant to rotation and translation.
In the following parts, we will firstly describe our flow-based generative model p
✓
(R|G) in Sec-
tion 3.2 and elaborate the energy-based tilting model E
(R, G) in Section 3.3. Then we introduce
the two-stage sampling process with both deterministic and stochastic dynamics in Section 3.4. An
illustration of the whole framework is given in Fig. 1.
3.2 FLOW-BAS E D GENERATIVE MODEL
Conditional Graph Continuous Flows p
✓
(d|G). We parameterize the conditional distribution of
distances p
✓
(d|G) with the continuous normalizing flow, named Conditional Graph Continuous
Flow (CGCF). CGCF defines the distribution through the following dynamics system:
d = F
✓
(d(t
0
), G)=d(t
0
)+
Z
t
1
t
0
f
✓
(d(t),t; G)dt, d(t
0
) ⇠ N(0, I) (6)
where the dynamic f
✓
is implemented by Message Passing Neural Networks (MPNN) (Gilmer et al.,
2017), which is a widely used architecture for representation learning on molecular graphs. MPNN
takes node attributes, edge attributes and the bonds lengths d(t) as input to compute the node and
edge embeddings. Each message passing layer updates the node embeddings by aggregating the
information from neighboring nodes according to its hidden vectors of respective nodes and edges.
Final features are fed into a neural network to compute the value of the dynamic f
✓
for all distances
independently. As t
1
!1, our dynamic can have an infinite number of steps and is capable to
model long-range dependencies. The invertibility of F
✓
allows us to not only conduct fast sampling,
but also easily optimize the parameter set ✓ by minimizing the exact negative log-likelihood:
L
mle
(d, G; ✓)=E
p
data
log p
✓
(d|G)=E
p
data
log p(d(t
0
)) +
Z
t
1
t
0
Tr
✓
@f
✓,G
@d(t)
◆
dt
. (7)
4
Mansimov, Elman, et al. "Molecular geometry prediction using a deep generative graph neural network." Scientific reports 9.1 (2019): 1-13.
Figure 2. Framework of CVGAE









