【多物理场材料属性应用】：有限元分析深入探索


# 摘要
多物理场分析是现代工程和技术研究中的一个关键领域，涉及到基础理论、数学原理、耦合分析实践、材料属性优化以及未来趋势与挑战。本文详细探讨了多物理场分析的理论基础，特别是有限元方法的数学原理及其在材料模型和本构关系中的应用。文章还深入分析了多物理场耦合分析的实践方法，包括数值模拟、材料属性在耦合分析中的应用及软件工具的实际案例研究。此外，本文提出了多物理场材料属性优化的策略，并通过实验验证和模型校准来提高分析准确性。最后，本文展望了多物理场分析的未来趋势，包括新兴材料的应用、高性能计算和跨学科融合的可能性。

# 关键字
多物理场分析；有限元方法；材料模型；耦合分析；材料属性优化；高性能计算

参考资源链接：[有限元分析用的材料属性表.pdf](https://wenku.csdn.net/doc/6401ac00cce7214c316ea448?spm=1055.2635.3001.10343)
# 1. 多物理场分析的基础理论

在现代工程和科学领域，多物理场分析已成为理解和预测复杂系统行为的关键工具。本章将概述多物理场分析的基础理论，为深入理解后续章节奠定基础。

## 1.1 多物理场分析的定义和重要性

多物理场分析涉及到两个或两个以上物理现象的相互作用，如热力、电磁、流体动力学等。通过这种分析，工程师和科学家可以模拟和理解这些现象在相互作用时的动态变化。

## 1.2 多物理场分析的工程应用

在实际工程应用中，多物理场分析帮助设计更加安全和高效的设备。例如，电子设备的热管理，需要结合热传导、热对流和热辐射等多种物理过程进行模拟。

## 1.3 分析过程和数值方法

多物理场分析通常需要将连续的物理现象离散化为可数值求解的形式。在众多的数值方法中，有限元方法因其适用性和灵活性而被广泛使用。

这一章的内容为后续章节的详细探讨提供了必要的理论基础，从而使得读者能够更好地理解多物理场分析在复杂系统建模中的应用和挑战。

# 2. 有限元方法的数学原理

### 2.1 有限元分析的数学基础
#### 2.1.1 变分原理与泛函分析

变分原理是有限元方法（Finite Element Method, FEM）的核心数学基础之一，它为工程问题的求解提供了理论依据。在FEM中，通过最小化一个能量泛函来找到一个近似解，这个能量泛函与问题的物理行为密切相关。

**变分原理**的数学表述通常涉及到对某个泛函的极小化问题。例如，对于一个弹性的静力学问题，可以将总势能泛函定义为应变能与外力势能之和。对于离散系统，一个典型的泛函可能表示为：

\[ \Pi(u) = \frac{1}{2} u^T K u - u^T f \]

其中，\( u \) 是位移向量，\( K \) 是刚度矩阵，\( f \) 是力向量。最小化这个泛函将给出位移场的解。

在泛函分析中，泛函\( \Pi(u) \)需要满足一定的条件，如连续性、可微性和强制性。在实际应用中，通常使用的是弱形式变分原理，这涉及到对泛函进行部分积分以减少解的连续性要求。

**代码块与逻辑分析：**

(* Mathematica代码示例：求解一个简单弹性力学问题的变分原理 *)
(* 定义能量泛函 *)
energyFunctional[u_] := 1/2 u\[Transpose].K.u - u\[Transpose].f;

(* 假设刚度矩阵K和力向量f是已知的 *)
K = {{4, -2}, {-2, 4}};
f = {1, 1};

(* 找到能量泛函的极小值 *)
minFunctional = Minimize[energyFunctional[u], u];
minFunctional

在上述的代码块中，我们定义了一个简单的能量泛函，并且对其进行了最小化处理，求解出了位移向量\( u \)的值。这个步骤在有限元分析的软件中是自动进行的，但这个过程展示了变分原理的数学基础。

在实际的有限元软件中，变分原理被转化为代数方程组，从而可以通过求解线性系统或非线性系统来找到近似解。这种方法不仅适用于线性问题，还可以推广到更复杂的非线性问题。

#### 2.1.2 线性代数在有限元中的应用

线性代数在有限元方法中扮演着至关重要的角色，因为它提供了一种形式化和解决大规模问题的框架。特别是矩阵运算和线性方程组的求解是有限元分析中不可或缺的部分。

**刚度矩阵**是线性代数应用中的一个核心概念，它代表了结构刚度的分布。刚度矩阵\( K \)通常是正定的，对称的，并且对于线性问题来说是常数矩阵。

**代码块与逻辑分析：**

% MATLAB代码示例：生成并求解线性系统
% 假设已知的刚度矩阵和载荷向量
K = [4 -2; -2 4];
f = [1; 1];

% 使用MATLAB的左除运算符求解线性方程组
u = K \ f;

% 显示结果
disp('位移向量 u:');
disp(u);

在这个MATLAB代码块中，我们使用了MATLAB的左除运算符来求解一个线性方程组。这种方法等价于应用高斯消元法或LU分解等线性代数算法。在有限元分析中，这种线性方程组通常更加庞大且稀疏，因此需要使用高效的数值线性代数算法来求解。

在大规模的多物理场问题中，刚度矩阵可能会非常庞大，这要求我们在构造和求解这些矩阵时必须采用高效的数值方法。例如，预处理共轭梯度法（Preconditioned Conjugate Gradient, PCG）就是一种有效的迭代解法，特别适用于大规模稀疏系统。

### 2.2 材料模型与本构关系

#### 2.2.1 材料属性的分类与定义

在有限元分析中，正确地描述材料的物理属性是非常重要的。材料属性通常可以分为两类：一类是线性属性，如杨氏模量、泊松比等；另一类是非线性属性，比如塑性、粘弹性等。

**线性材料属性**的数学描述相对简单，通常用线性本构方程来表示。例如，线性弹性材料的应力-应变关系可以表示为：

\[ \sigma = E \epsilon \]

其中，\( \sigma \) 是应力向量，\( \epsilon \) 是应变向量，而\( E \) 是杨氏模量。

**非线性材料属性**的描述则复杂得多，它们通常依赖于历史加载路径，比如塑性材料的行为不仅依赖于当前的应变状态，还取决于材料所经历的加载历史。非线性本构关系的数学表达可能涉及到复杂的函数或方程组，有时需要数值方法来求解。

**代码块与逻辑分析：**

import numpy as np

# Python代码示例：计算线性材料属性的应力
E = 210e9  # 杨氏模量，单位帕斯卡
epsilon = np.array([0.001, 0.002, -0.0005])  # 应变向量

# 使用线性本构模型计算应力
sigma = E * epsilon

print("应力向量 sigma:")
print(sigma)

在上述Python代码中，我们使用了线性本构模型来计算给定应变向量下的应力向量。对于非线性材料属性的描述和计算，通常需要更复杂的数值算法，可能包括迭代方法和非线性求解器。

在有限元软件中，定义材料属性通常通过用户界面进行，软件会根据用户的定义来建立相应的本构模型，并在后处理中展示结果。

#### 2.2.2 热-结构耦合的本构模型

热-结构耦合是指热能和机械能之间相互作用的问题，例如，热膨胀或热引起的应力。这种耦合问题在有限元分析中非常重要，尤其是在材料或结构在热载荷下发生显著形变时。

一个基本的热-结构耦合本构模型可以使用热弹性理论来表达。在小变形假设下，热弹性问题可以基于线性弹性本构关系和热膨胀方程来描述。对于给定的温度场\( T \)，热应变可以表示为：

\[ \epsilon_{\text{th}} = \alpha (T - T_0) I \]

其中，\( \alpha \)是材料的热膨胀系数，\( T_0 \)是参考温度，\( I \)是单位矩阵。

在有限元软件中，热-结构耦合分析需要同时求解温度场和位移场，这通常是通过求解一系列的耦合偏微分方程来实现的。

**代码块与逻辑分析：**

*HEADING
** 热-结构耦合有限元分析的Abaqus输入文件示例
** 定义材料属性
*MATERIAL, NAME=MyMaterial
*ELASTIC
 210e9, 0.3
*EXPANSION
 1.2e-5
** 其他定义...

上述代码为一个Abaqus输入文件的片段，描述了一个具有热膨胀属性的材料定义。Abaqus等软件可以自动处理材料的热-结构耦合效应。

在进行实际的热-结构耦合分析时，需要定义适当的边界条件、载荷和材料属性，并运行分析。分析完成后，软件会提供位移场和温度场的结果，以及可能的应力和应变信息。

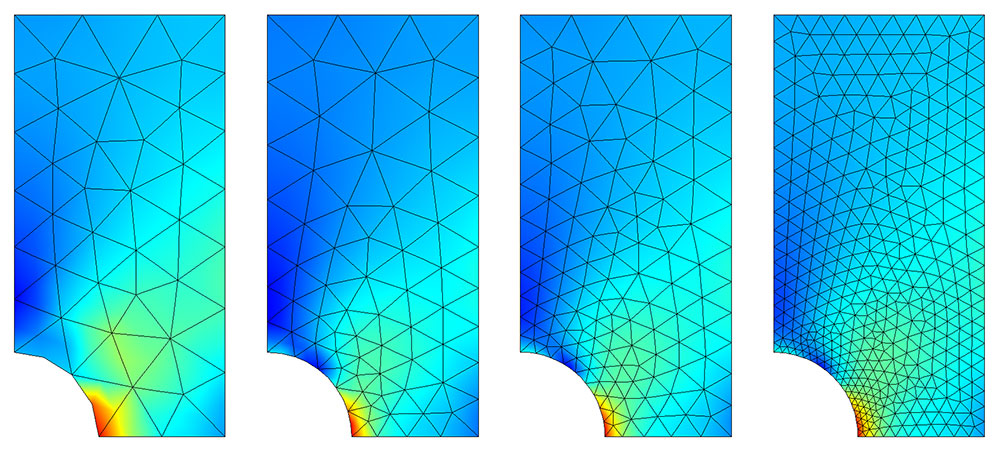
### 2.3 网格划分技术

#### 2.3.1 网格类型与选择标准