理解数字电路基础：第一章数制与码制详解

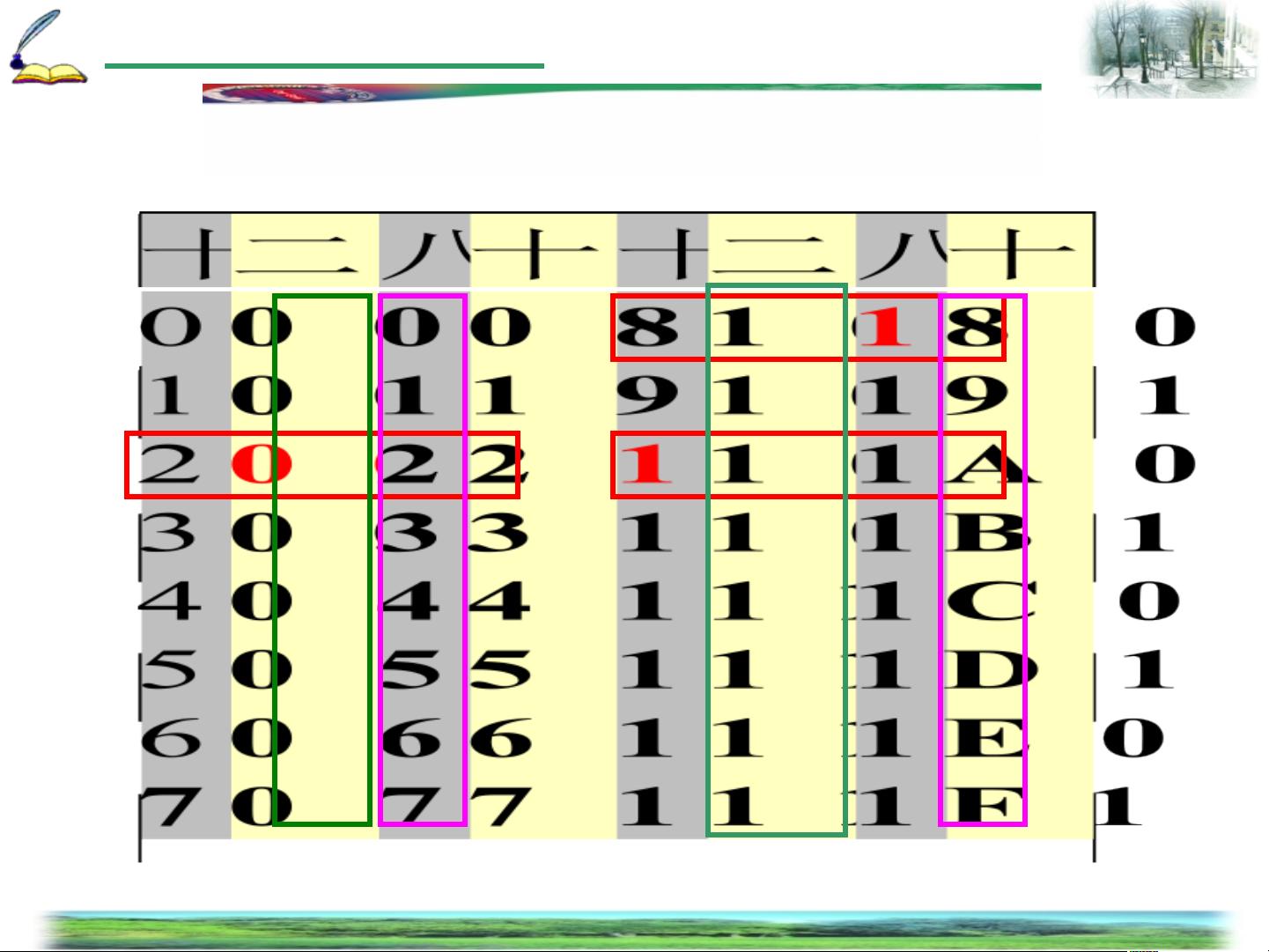
本篇数字电路课件主要讲解了第一章的内容——数制和码制。数制是任何进位计数系统的基石，它定义了每位数字的构成方式以及数位间的进位规则。常见的数制包括十进制（基数10，逢十进一）、二进制（基数2，逢二进一）和八进制、十六进制等。数制的表示通常有两种形式：位置计数法和按权展开式。 位置计数法是将数字按照其在数位中的位置赋予相应的数值，从最低位（最右边）开始，每个位置的数值是基数的幂次。例如，在十进制中，\( (173.23)_{10} \) 的位置计数表示为 \( 1 \times 10^2 + 7 \times 10^1 + 3 \times 10^0 + 2 \times 10^{-1} + 3 \times 10^{-2} \)。 按权展开式则是利用每位数符乘以对应的基数的幂次来表示数值，例如二进制的 \( (10101)_{2} \) 可以写成 \( 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 \)。这里要注意，数位上的权值是基数的指数，如二进制的 \( 2^i \)，随着数位由右向左递减，其值也相应减小。 课程中强调了基数（R）的概念，它是数制中的核心要素，决定了每一位数的最大值。例如，十进制的基数是10，所以最大数位上的数值只能是9（10-1）。不同数制之间的转换是电子工程和计算机科学中的基础操作，理解这些概念对于处理和解析二进制数据尤其重要，因为计算机内部的运算几乎都是基于二进制进行的。 此外，课程还提到了编码，这是将信息以特定的数字代码表示的过程，比如常用的ASCII码（美国标准信息交换码）就是一种字符编码，将字母、数字和特殊符号映射到二进制数上，便于存储和传输。 通过学习第一章的数制和码制，学生将能够掌握不同数制的基本原理，理解数字在计算机世界中的基本表示形式，并能进行有效的数字转换和编码操作。这对于后续深入研究数字电路设计、计算机组成原理等课程至关重要。