自由曲面照明光学设计综述：突破传统，推动工程发展
需积分: 10 201 浏览量
更新于2024-07-15
收藏 7.48MB PDF 举报
"《自由曲面照明光学设计》是一篇关于新兴技术——自由形式光学的综述文章，该技术正在推动照明设计领域的革新。传统的光学设计受到表面几何形状的限制，而自由形式光学则打破了这种束缚，使得设计师和工程师能够创造出更紧凑、轻便且效率高的照明系统，同时保持卓越的光学性能。本文的焦点在于自由形式照明光学设计，这是推动照明工程发展的重要驱动力。
设计方法主要分为两大类：一类是基于理想光源假设的零固有通量算法，如射线映射法、 Monge-Ampère 方程方法以及支撑二次曲面方法。这些算法强调了对理想光源的理想化处理，旨在实现最优化的光线分布和控制。
另一类是针对扩展光源的设计算法，这类方法考虑到了实际光源的特性，如大小、形状和发射特性。这些算法更加注重如何在复杂场景中有效分布和控制光线，以满足不同应用场景的需求，比如在照明、投影、成像等领域的实际应用中。
学习和实践自由形式照明光学设计，不仅需要掌握理论基础，还要灵活运用各种设计工具和软件，如光场模拟软件、非球面加工技术等。此外，随着技术的发展，新型材料和制造工艺也对设计提出了更高的要求。对于刚入门的光学工程师来说，通过不断学习、交流和实践，可以在这个领域不断成长，共同推进照明技术的进步。
本文提供了一个全面的视角，适合照明设计初学者参考，同时也为深入研究者提供了丰富的研究资源和实践指导。阅读和研究这篇论文，有助于理解和掌握自由形式照明光学设计的关键技术和策略，为未来的照明工程设计创新奠定坚实的基础。"
www.advancedsciencenews.com www.lpr-journal.org
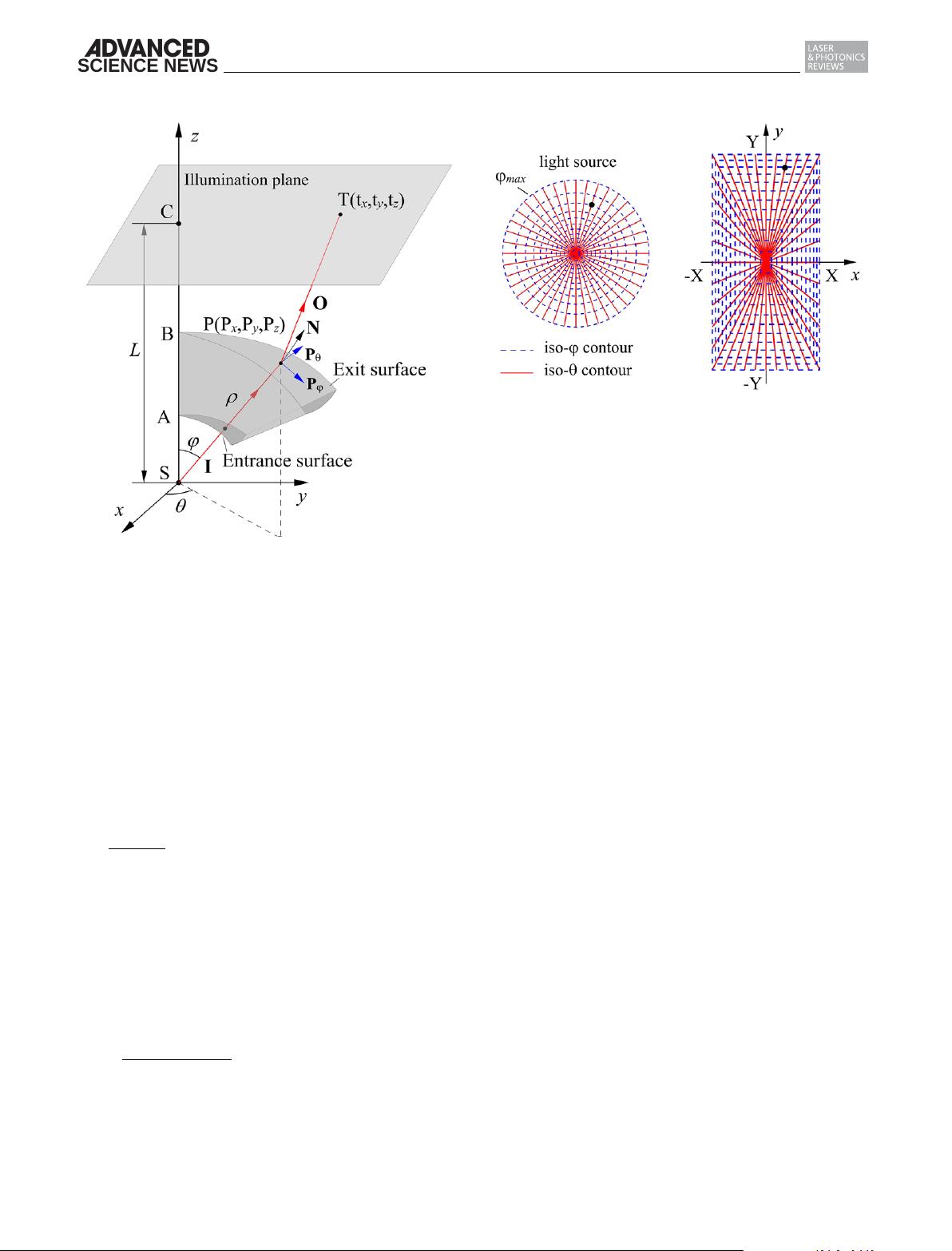
Figure 2. Geometrical design layout of the freeform lens.
the entrance surface, the unit vector of the incident ray can be
written as
I =
(
sin ϕ cos θ,sin ϕ sin θ,cos ϕ
)
(1)
Then, we know that the position vector of point P is given by
P = ρ × I (2)
Taking the first partial derivative of P with respective to θ and ϕ
yields two tangent vectors at point P along θ and ϕ directions. The
cross product of these two tangent vectors gives us the normal to
the freeform surface at point P, which can be written as
N =
P
ϕ
× P
θ
P
ϕ
× P
θ
(3)
where P
ϕ
and P
θ
are the two tangent vectors at point P. We as-
sume that O is the unit vector of the outgoing ray. It is apparent
that the three vectors I, O and N should obey Snell’s law, which
means the three vectors should satisfy Equation (4)
O = nI + P
1
N (4)
where n is the refractive index of the freeform lens and the pa-
rameter P
1
is given by
P
1
=
1 − n
2
+ n
2
(
I · N
)
2
− n
(
I · N
)
Here, the black dot in the equation above denotes the dot prod-
uct of two vectors. Equations (3) and (4) show clearly that the three
components of O given by Equation (4) are functions of ρ, θ , ϕ,
Figure 3. A variable separation mapping. A prescribed uniform rectangu-
lar illumination is defined on the domain [−X, X] × [−Y, Y ]. X = 5 mm, Y =
10 mm and the lighting distance between the source and the illumination
plane equals 10 mm. The refractive index of the lens equals 1.59. The light
rays from a Lambertian point source are directed by the freeform lens to
produce the prescribed illumination.
ρ
θ
and ρ
ϕ
.Hereρ
θ
and ρ
ϕ
are the first-order derivatives of ρ with
respective to θ and ϕ. It should be noted that ρ
θ
and ρ
ϕ
are also
the functions of ρ, θ and ϕ. After we calculate the vector O,we
can get the x and y coordinates of point T, t
x
and t
y
. Likewise, t
x
and t
y
are also functions of ρ, θ, ϕ, ρ
θ
and ρ
ϕ
. We assume that t
x
and t
y
can be written as
t
x
= f
1
ρ,θ,ϕ,ρ
θ
,ρ
ϕ
t
y
= f
2
ρ,θ,ϕ,ρ
θ
,ρ
ϕ
(5)
Equation (5) tells us that the location of the intersection point
of the outgoing ray on the illumination plane is fully determined
by the surface profile. Solving Equation (5) for ρ
θ
and ρ
ϕ
gives us
ρ
θ
and ρ
ϕ
ρ
θ
= g
1
ρ,θ,ϕ,t
x
, t
y
ρ
ϕ
= g
2
ρ,θ,ϕ,t
x
, t
y
(6)
Since t
x
and t
y
are functions of θ and ϕ, the two partial
differential equations in Equation (6) become solvable only if
the relationship between point T and the vector I is known.
That is to say we need to choose a ray mapping which specifies
where an incident ray should go after refraction by the freeform
lens. Choosing a ray mapping is the key step in the ray mapping
method.
[50,51,54]
A ray mapping can be determined by the conser-
vation law of energy and this usually yields an infinite number
of possible ray mappings. An easy mapping to compute (but that
will not lead to a desirable solution) is obtained if a separation
of variables is applied.
[50,51,54]
Figure 3 gives a variable separation
mapping used to design a freeform lens which produces a uni-
form rectangular illumination on a target plane. The ray mapping
Laser Photonics Rev. 2018, 1700310
C
2018 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim1700310 (4 of 18)
剩余17页未读，继续阅读
2018-03-06 上传
2021-02-07 上传
2014-05-29 上传
2021-08-05 上传
2021-02-11 上传
2019-12-18 上传
2023-11-13 上传
2019-07-17 上传
right_and
- 粉丝: 0
- 资源: 1
我的内容管理
展开
最新资源
- 新代数控API接口实现CNC数据采集技术解析
- Java版Window任务管理器的设计与实现
- 响应式网页模板及前端源码合集：HTML、CSS、JS与H5
- 可爱贪吃蛇动画特效的Canvas实现教程
- 微信小程序婚礼邀请函教程
- SOCR UCLA WebGis修改：整合世界银行数据
- BUPT计网课程设计：实现具有中继转发功能的DNS服务器
- C# Winform记事本工具开发教程与功能介绍
- 移动端自适应H5网页模板与前端源码包
- Logadm日志管理工具：创建与删除日志条目的详细指南
- 双日记微信小程序开源项目-百度地图集成
- ThreeJS天空盒素材集锦 35+ 优质效果
- 百度地图Java源码深度解析：GoogleDapper中文翻译与应用
- Linux系统调查工具：BashScripts脚本集合
- Kubernetes v1.20 完整二进制安装指南与脚本
- 百度地图开发java源码-KSYMediaPlayerKit_Android库更新与使用说明
