决策树算法详解：特征选择与剪枝策略

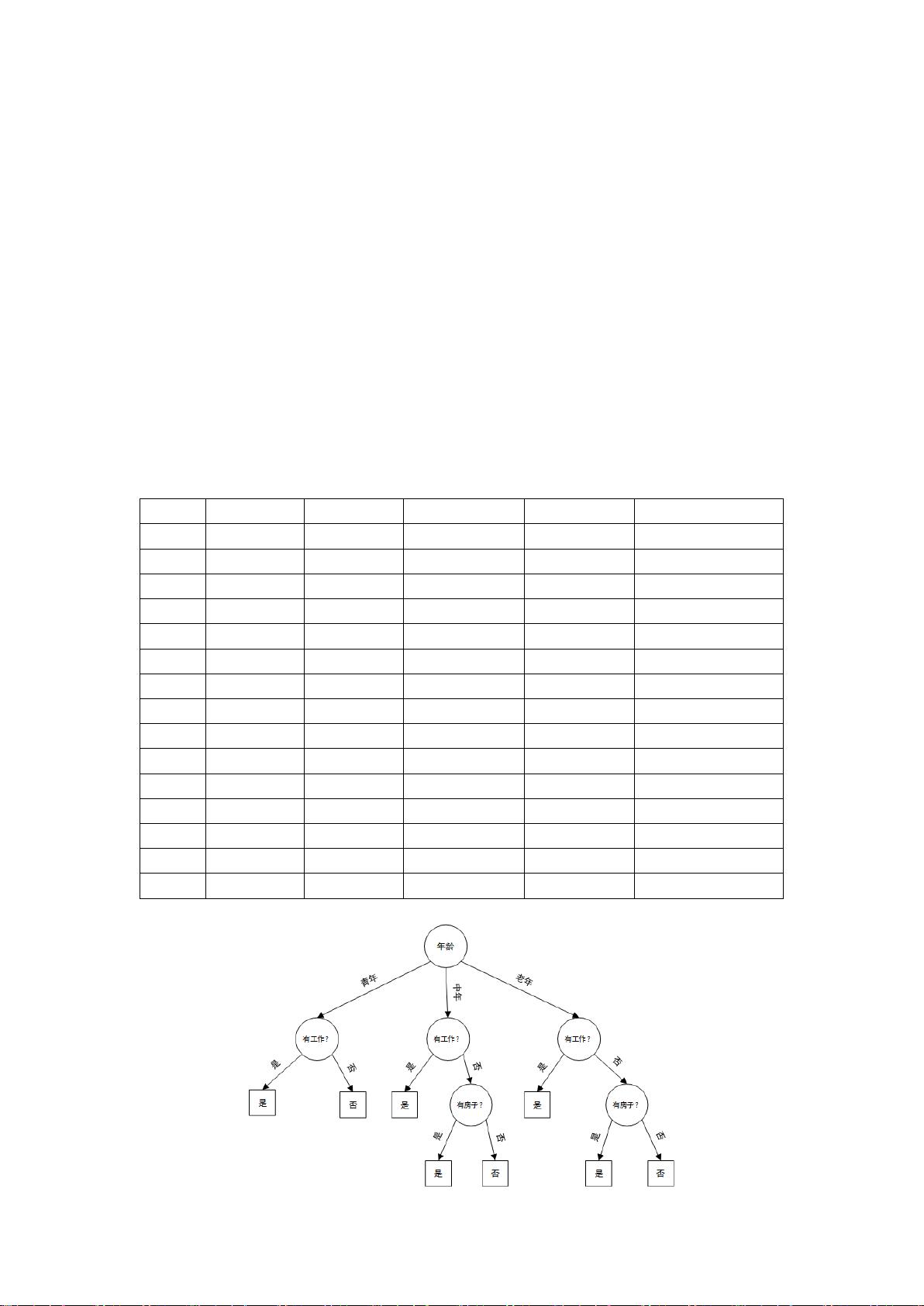
决策树分类算法原理深入解析 决策树是一种基于“分而治之”策略的机器学习算法，特别适用于分类任务，同时也可用于回归分析。其基本流程包括特征选择、决策树生成和剪枝三个步骤。文档介绍了ID3、C4.5和CART这三种经典的决策树算法，它们的主要区别在于特征选择的准则。 在特征选择过程中，信息增益、信息增益率和基尼指数是常用的定量评估标准。信息增益衡量的是某个特征在给定数据集中对分类的纯度提升，即\( g(D,A) = H(D) - H(D|A) \)，其中\( H(D) \)是数据集的整体不确定性，\( H(D|A) \)是特征A条件下子集的不确定性。信息增益率考虑了特征的纯度提升相对于特征引入的复杂性，而基尼指数则反映了分类不纯度，用于衡量不确定性。 以贷款申请人的案例为例，假设数据集包含年龄、工作状态、住房状况和信贷情况四个特征。通过不同的特征排序，决策树的结构会有所变化。例如，按照年龄-工作-房子-信贷或工作-房子-年龄-信贷的顺序构建，可能会得出不同复杂度的决策树。通常，选择具有最高信息增益或信息增益率的特征作为分割点，可以生成更简单的树，提高分类效率。 然而，特征选择并非总是直接根据这些指标，还需要结合实际问题的业务理解，以及避免过拟合。剪枝过程是防止过度拟合的重要环节，它通过在决策树生成后删除或合并某些内部节点来简化模型。CART算法采用的是代价复杂度或基尼指数剪枝，以找到最佳平衡点。 决策树分类算法的核心在于合理选择特征和适时剪枝，以实现模型的高效性和可解释性。通过信息增益等量化方法，我们可以优化特征选择过程，最终构建出既能有效分类又具有可理解性的决策树模型。这对于实际问题中的预测和决策支持具有重要意义。