数字信号处理：快速傅里叶变换FFT详解

"快速傅里叶变换精讲——讲解了快速傅里叶变换(FFT)在数字信号处理中的重要性，以及如何通过基2 FFT算法大幅降低计算复杂度" 快速傅里叶变换（FFT）是一种高效计算离散傅里叶变换（DFT）的算法，对于信号分析和处理至关重要。在数字信号处理（DSP）领域，FFT的运用极大地提升了计算效率，使得大规模数据的实时处理成为可能。1965年，FFT算法的发现将DFT的运算效率提升了1-2个数量级，为数字信号处理技术的实际应用奠定了基础。之后在1984年，分裂基快速算法的提出进一步优化了运算效率。 DFT是分析有限长序列的关键工具，它的计算量与序列长度N的平方成正比，这意味着当N增大时，计算量急剧增加。为了降低计算复杂度，人们寻求将N点DFT分解为更短的DFT，同时利用旋转因子W_mN的周期性和对称性进行合并和简化，以减少乘法次数。 基2 FFT算法是FFT算法的一种实现方式，它主要通过时域抽取法（DIT-FFT）和频域抽取法（DIF-FFT）。时域抽取法将原始序列按n的奇偶分成两组，每组进行N/2点的DFT计算，然后组合得到N点的DFT。这种方法的关键在于序列分解和旋转因子的利用。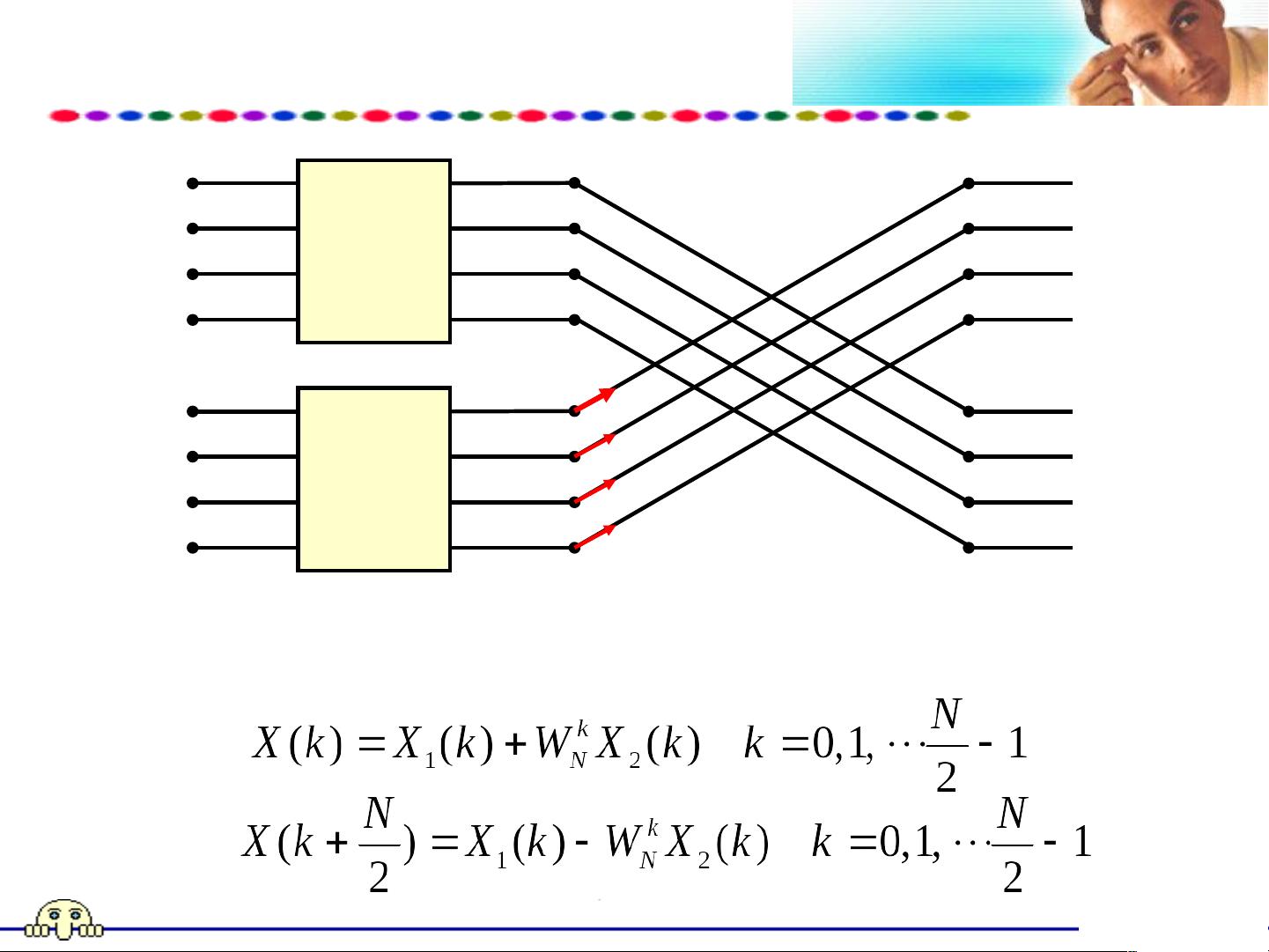 在时域抽取法中，序列x(n)首先被分为x1(n)和x2(n)，这两部分分别对应n为奇数和偶数的元素。然后对x1(n)和x2(n)分别进行N/2点的DFT，得到X1(k)和X2(k)。最后，通过一定的公式组合X1(k)和X2(k)来得到原始序列x(n)的N点DFT X(k)。 在分解过程中，旋转因子W_mN的周期性和对称性起到了关键作用。W_mN具有周期性，即W_mN = W_{m+N}(k)，并且在某些情况下可以利用对称性减少乘法操作。例如，当N是2的幂时，可以将旋转因子分为实部和虚部，利用它们的对称性进行合并，进一步减少运算量。 快速傅里叶变换通过巧妙的序列分解和旋转因子的特性，显著降低了DFT的计算复杂度，从而在信号处理、图像分析、通信等多个领域得到了广泛应用。理解并熟练掌握FFT算法是数字信号处理中的必备技能。