拉格朗日插值法详解：构建数据点间的多项式桥梁

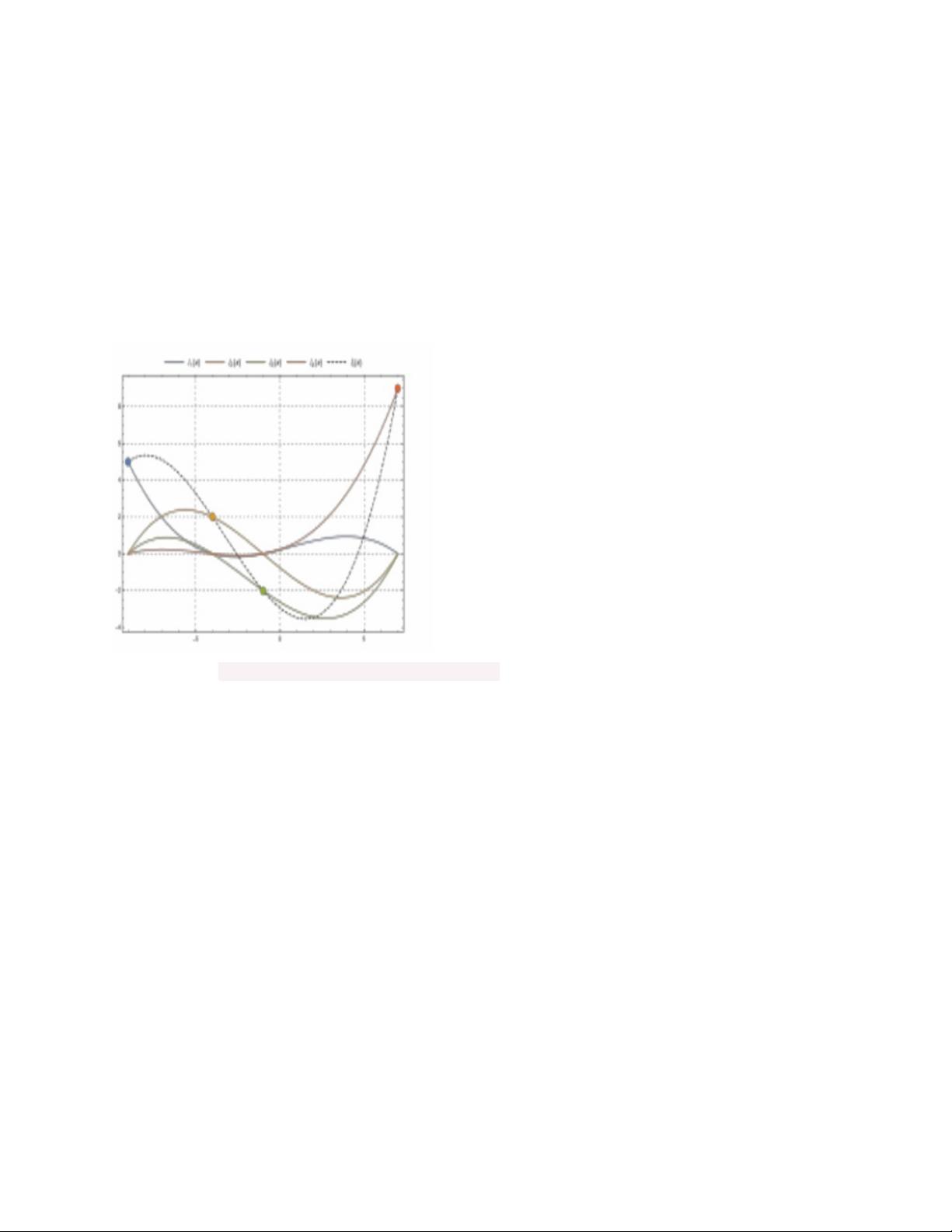
拉格朗日插值法是数值分析中的一个重要工具，源自十八世纪数学家约瑟夫·拉格朗日的贡献。它是一种多项式插值技术，特别适用于在没有解析表达式的函数数据点上构建近似模型。在实际应用中，例如物理测量、工程设计或数据分析中，当我们需要根据有限数量的实验数据拟合一个函数时，拉格朗日插值法显得尤为有用。 该方法的核心概念是基于一组已知数据点来确定一个特定次数的多项式，这个多项式能够在这些点上精确地取到给定的函数值。对于给定的n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，拉格朗日插值公式构造了一个唯一的多项式L(x)，使得L(xi) = yi，对于所有的i = 0, 1, ..., n。 拉格朗日基本多项式Lλ(x)是拉格朗日插值的核心，它的定义是对于每个数据点(i)，它是这样一个函数，当x等于数据点的坐标xi时，取值为1，而在其他点上的值为0。这种特性使得每个基本多项式能够"锁定"一个数据点。拉格朗日插值多项式L(x)就是这些基本多项式的线性组合，其形式为： L(x) = Σ[λi(x) * yj]，其中λi(x) = Π[(x - xk) / (xi - xk)] for k ≠ i 通过计算每个λi(x)，我们可以将函数值yi与对应的系数相乘，然后求和，得到插值函数。例如，若我们要对一个二次多项式函数在(x0, y0), (x1, y1), (x2, y2)这三个点上的值进行插值，我们首先写出每个基本多项式，然后将这些多项式与对应的y值相乘，最后代入拉格朗日插值公式求解。 拉格朗日插值法的优点是简单直观，但需要注意的是，随着数据点的数量增加，插值多项式的次数也会相应增加，可能导致计算复杂度提高。此外，对于过于密集或离散的数据点，高次多项式可能会出现过度拟合，影响插值结果的稳定性和泛化能力。因此，在实际应用中，可能需要结合其他插值方法或统计学习方法进行综合考虑。 拉格朗日插值法是基础的数值分析工具，对于理解函数行为、数据拟合以及数值计算都有着重要的作用。掌握这一方法，有助于我们在处理实际问题时更准确地利用有限的数据进行函数逼近。