线性代数解析：矩阵变换与特征值特征向量

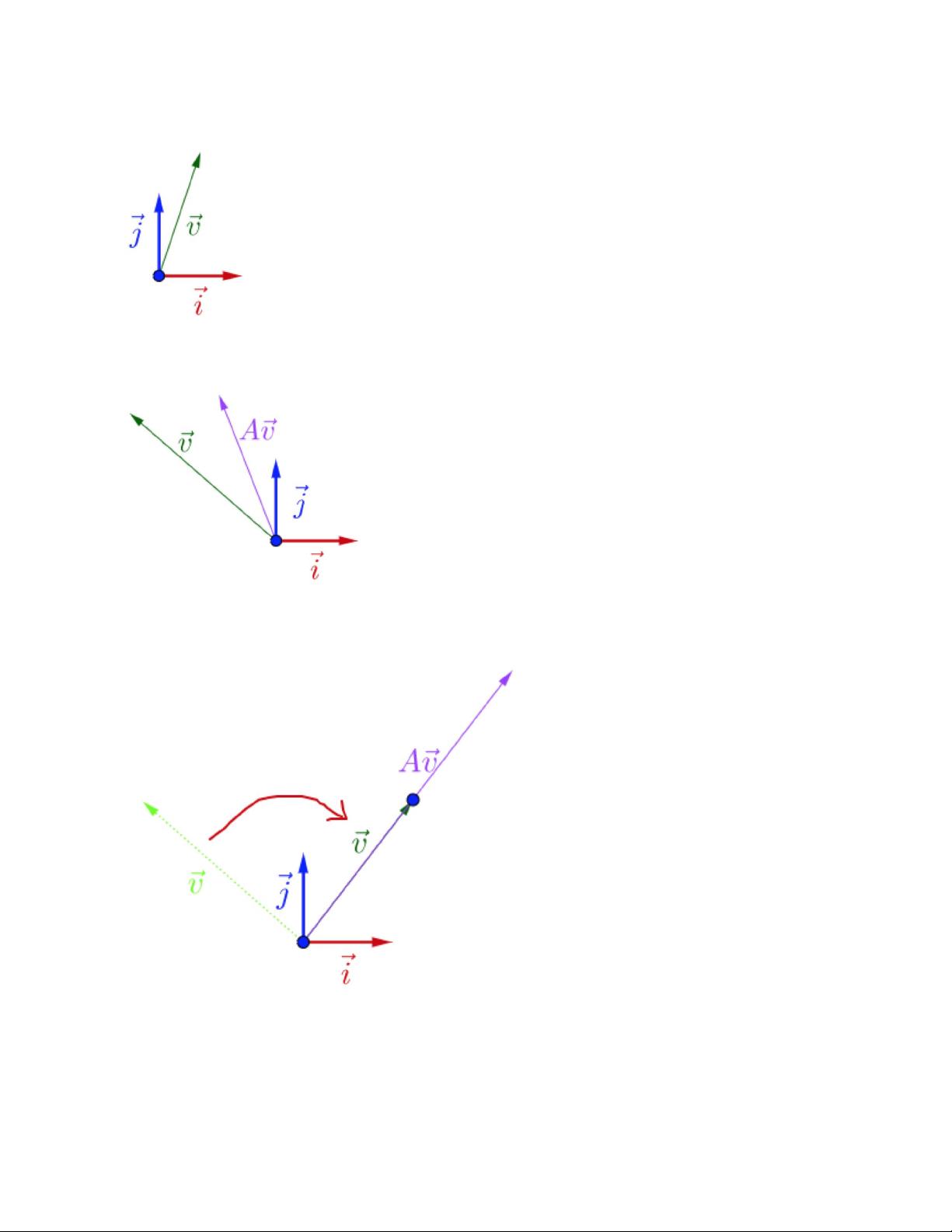
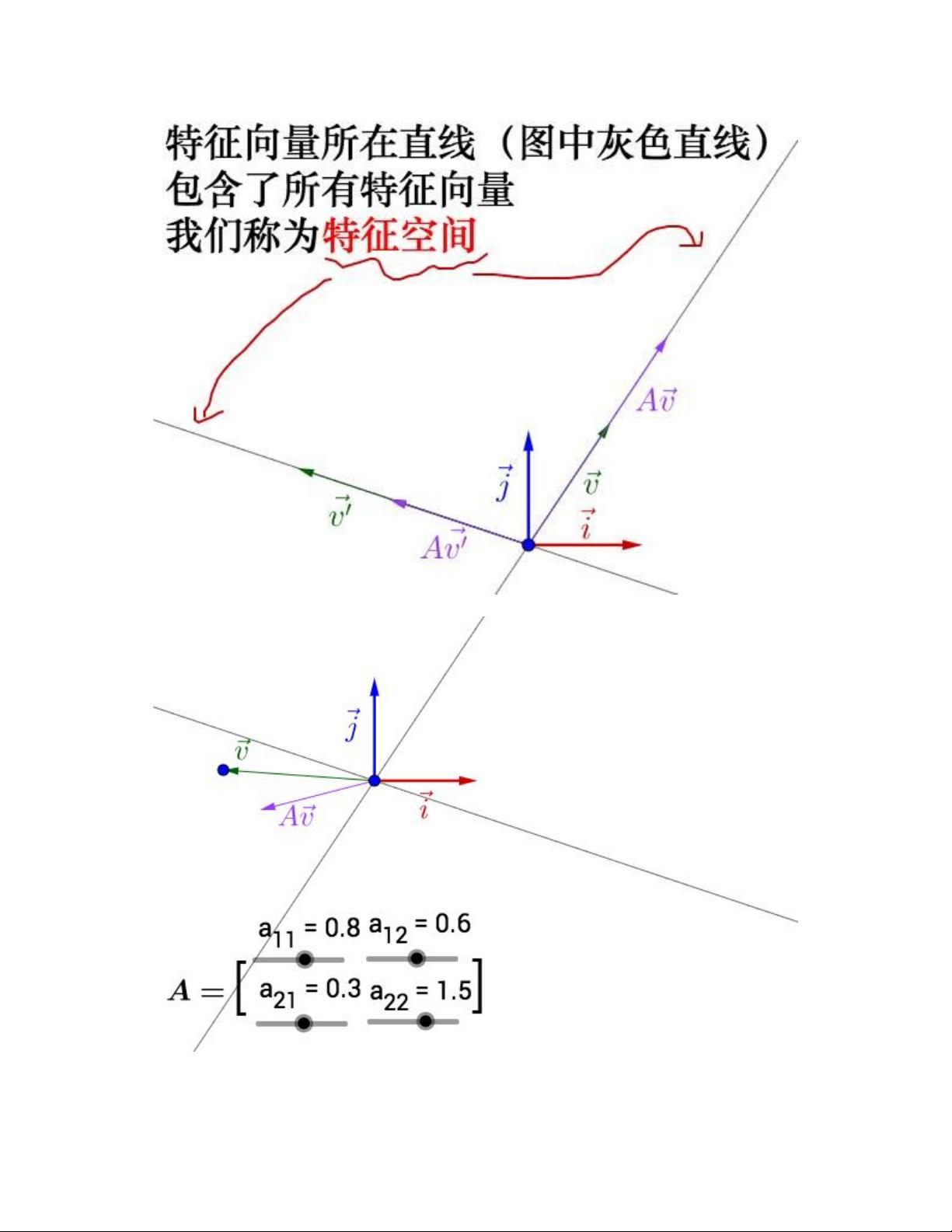
"这篇线性代数笔记详细探讨了矩阵变换的几何解释，以及矩阵分解的几何意义。它强调了对角矩阵、三角矩阵和正交矩阵在几何变换中的作用，同时也介绍了矩阵特征值和特征向量的概念。" 在机器学习和数据科学中，线性代数是不可或缺的基础。这篇笔记首先解释了为何要将矩阵分解为因子矩阵，特别是对角矩阵、三角矩阵和正交矩阵。对角矩阵的乘法相当于对坐标轴进行独立缩放，其中正数表示伸长，负数表示反向缩放，而零则表示空间压缩。三角矩阵，包括上三角和下三角，引入了切变效果，分别表现为右上角的斜拉和左下角的斜推。正交矩阵则保持物体形状不变，仅进行旋转。 接着，笔记阐述了矩阵分解的几何意义，如LU、LDU、LL、LDL分解及QR、SVD分解，这些分解方法将矩阵作用分解为一系列简单的几何变换。例如，LU和LL分解主要处理三角矩阵，而QR和SVD分解涉及正交矩阵和对角矩阵。这种分解有助于理解和简化复杂的矩阵运算。 特征值和特征向量是矩阵理论的核心概念。在实数范围内，特征值可以被理解为矩阵动作的速度，而特征向量则代表了这个“速度”沿的方向。特征值和特征向量提供了矩阵动力学的直观描述，揭示了矩阵作用下的动态行为。在实际应用中，例如在数据分析和机器学习模型中，特征值和特征向量经常用于主成分分析（PCA）、奇异值分解（SVD）等技术，以便提取数据的主要特征或降低数据的维度。 这篇线性代数笔记通过几何解释深入浅出地解析了矩阵变换的本质，为学习者提供了一个理解和应用线性代数基础知识的有力工具。无论是初学者还是经验丰富的专业人士，都能从中受益，更好地掌握线性代数在机器学习领域的应用。