离散信号卷积计算：竖式乘法与图表法

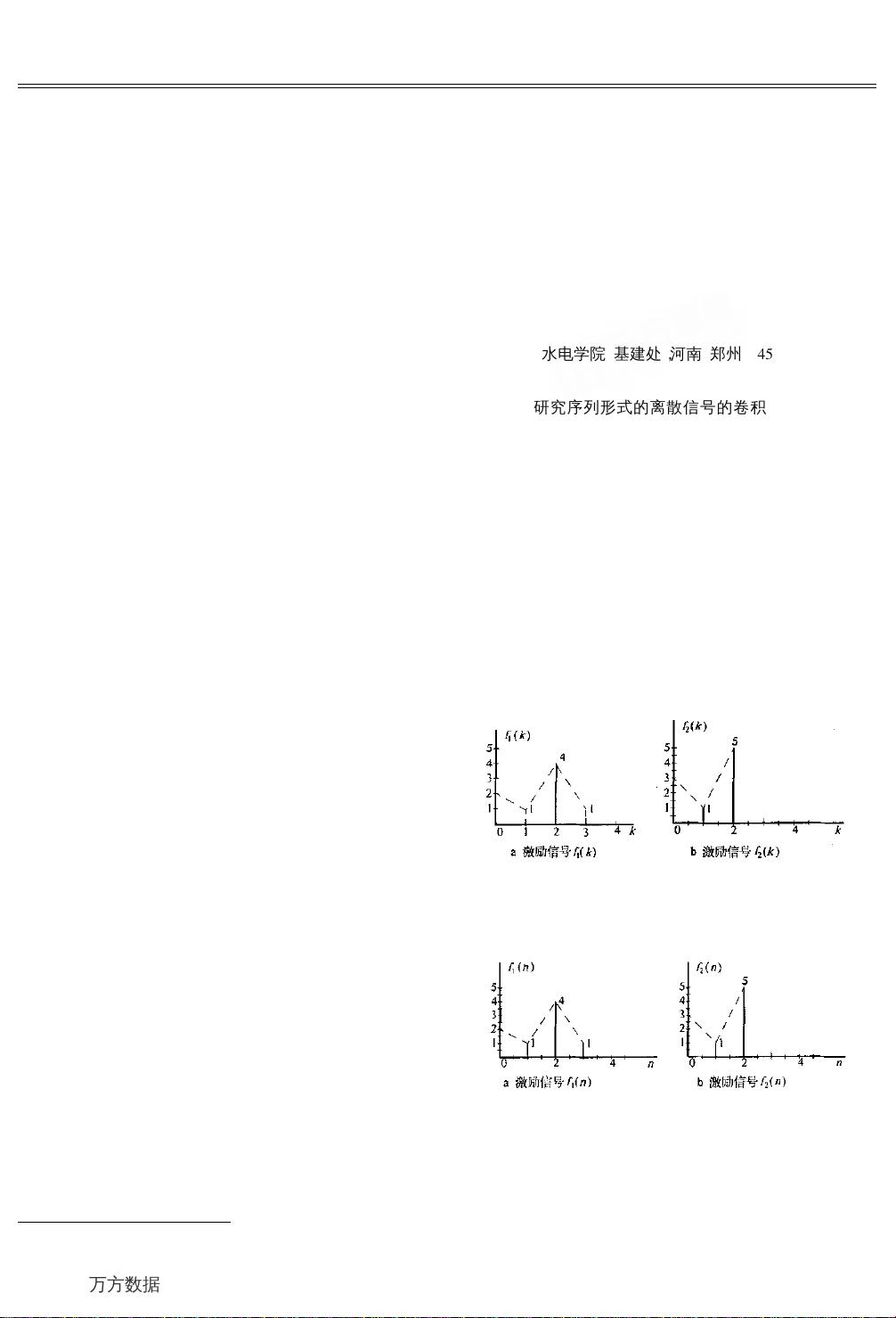
"如何简便快速计算离散信号的卷积" 离散信号的卷积是数字信号处理中的核心概念，尤其在通信、图像处理和信号滤波等领域有着广泛应用。离散卷积是两个离散时间序列的数学组合，它反映了一个序列通过线性时不变系统后的输出响应。本文主要探讨了如何简化离散信号卷积的计算过程。 离散信号卷积的定义通常表示为两个序列 !K(") 和 !!"(") 的乘积之和，即： S(!) = ∑[!K("!) * !!"("! - $)] 其中，$ 是一个时间变量，表示序列 !!(") 的平移。为了计算卷积，需要对序列 !!(") 进行反折 (!!"("%$)) 和平移 (!!"("%$))，然后与序列 !K($) 进行逐点乘积，并对所有结果求和。这个过程可以形象地用图解法来完成，但这种方法比较耗时且容易出错。 文章中提出了一种更为简便的运算方法——竖式乘法和图表法。这两种方法都旨在简化计算流程，提高效率。竖式乘法类似于我们熟悉的算术乘法，将序列 !K($) 竖直排列，序列 !!("$) 反折后水平放置，然后逐点相乘并按位置相加，得到最终的卷积结果。图表法则通过绘制序列图形，直观地进行反折、平移和乘积操作，再累加各个区域的面积，从而得出卷积值。 竖式乘法的优点在于，它可以避免手动平移和反折的复杂操作，只需简单的乘法和加法运算，尤其适用于计算机程序实现。而图表法则更适用于理解和教学，帮助人们直观理解卷积的过程。 在实际应用中，离散信号卷积的计算可以通过编程语言如MATLAB或Python的库函数实现，大大提高了计算速度和精度。然而，对于初学者来说，理解并掌握竖式乘法和图表法仍然十分有益，它们能够帮助深入理解卷积的原理，同时也为以后的高级算法打下坚实基础。 离散信号卷积是信号处理的关键工具，学习简便快速的计算方法有助于提高工作效率。通过竖式乘法和图表法，我们可以更高效地处理离散信号的卷积问题，为现代通信技术及其他相关领域的应用提供便利。