1.3 Paper Organization
In Section 2, we give preliminaries used throughout this
paper. The outline of the scheme is presented in Section 3. In
Section 4, we present a security model of our scheme. In Sec-
tion 5, a concrete construction is given. In Section 6, we give a
security analysis about our scheme. Section 7 shows an experi-
ment for our scheme. We conclude our paper in Section 8.
2PRELIMINARIES
2.1 Bilinear Pairings [29]
Let G and G
T
be cyclic groups with prime order p. A bilin-
ear map e : G G ! G
T
has the following properties.
1) Bilinearity. 8g
1
;g
2
2 G, eðg
a
1
;g
b
2
Þ¼eðg
1
;g
2
Þ
ab
, where
a; b 2 Z
p
.
2) Non-degeneracy. eðg
1
;g
2
Þ 6¼ 1.
3) Computability. There is an efficient algorithm to
compute eðg
1
;g
2
Þ.
2.2 Divisible Computation Diffie-Hellman (DCDH)
Assumption [34]
DCDH Problem. Let G be a group with prime order p. g is a
generator in G. For a given tuple g; g
a
;g
b
where a; b 2 Z
p
.
The DCDH problem is to output g
a=b
.
DCDH Assumption. We say that DCDH assumption holds
if no probabilistic polynomial time (PPT) adversaries can
solve the DCDH problem with at most a negligible advantage.
The DCDH Problem is an equivalent variation of compu-
tational Diffie-Hellman problem [34].
2.3 Access Structure [30]
Let P ¼fP
1
;P
2
; ...;P
n
g be a set of parties. A collection A
2
P
is monotone if 8B; C : if B 2 A and B C then C 2 A.An
access structure is a collection A for non-empty subsets of P ,
i.e., A 2 2
P
nf;g. The sets in A are named the authorized sets,
and the sets not in A are named the unauthorized sets.
2.4 Ciphertext-Po licy Attribute-Based Encryption
A basic CP-ABE scheme [4] concludes the following funda-
mental algorithms:
SetupðÞ. This algorithm takes a security parameter as
input. It outputs a public parameter PK and a master key
MK.
EncryptðPK; M; AÞ. This algorithm takes the public
parameter PK, a message M, and an access policy A in the
attribute universe as input. The algorithm outputs a cipher-
text CT such that only the user whose attribute set satisfies
the access policy can decrypt. We assume that the ciphertext
implicitly includes A.
KenGenðMK; SÞ. This algorithm takes the master key
MK and an attribute set S as input. It outputs a private key
SK with respect to the attribute set S.
DecryptðPK; CT; SKÞ. This algorithm takes the public
parameter PK, a ciphertext CT, and a private key SK as
input. If the user’s attribute set S satisfies the access struc-
ture A embedded in the CT , then the algorithm decrypts the
ciphertext successfully and returns M.
2.5 Proxy Re-Encryption
Proxy re-encryption [31] allows an honest-but-curious
proxy to convert a ciphertext encrypted by Alice’s public
key into a new ciphertext that is able to be decrypted by
Bob’s secret key. In this process, the proxy is unable to get
the underlying plaintext. More formally, a proxy re-encryp-
tion scheme enables the proxy with the proxy re-encryption
key to translate ciphertext encrypted by public key pk
a
into
ciphertext encrypted by public key pk
b
.
3OUTLINE OF CP-ABE WITH EFFICIENT USER
REVOCATION
3.1 Explanation of Symbols
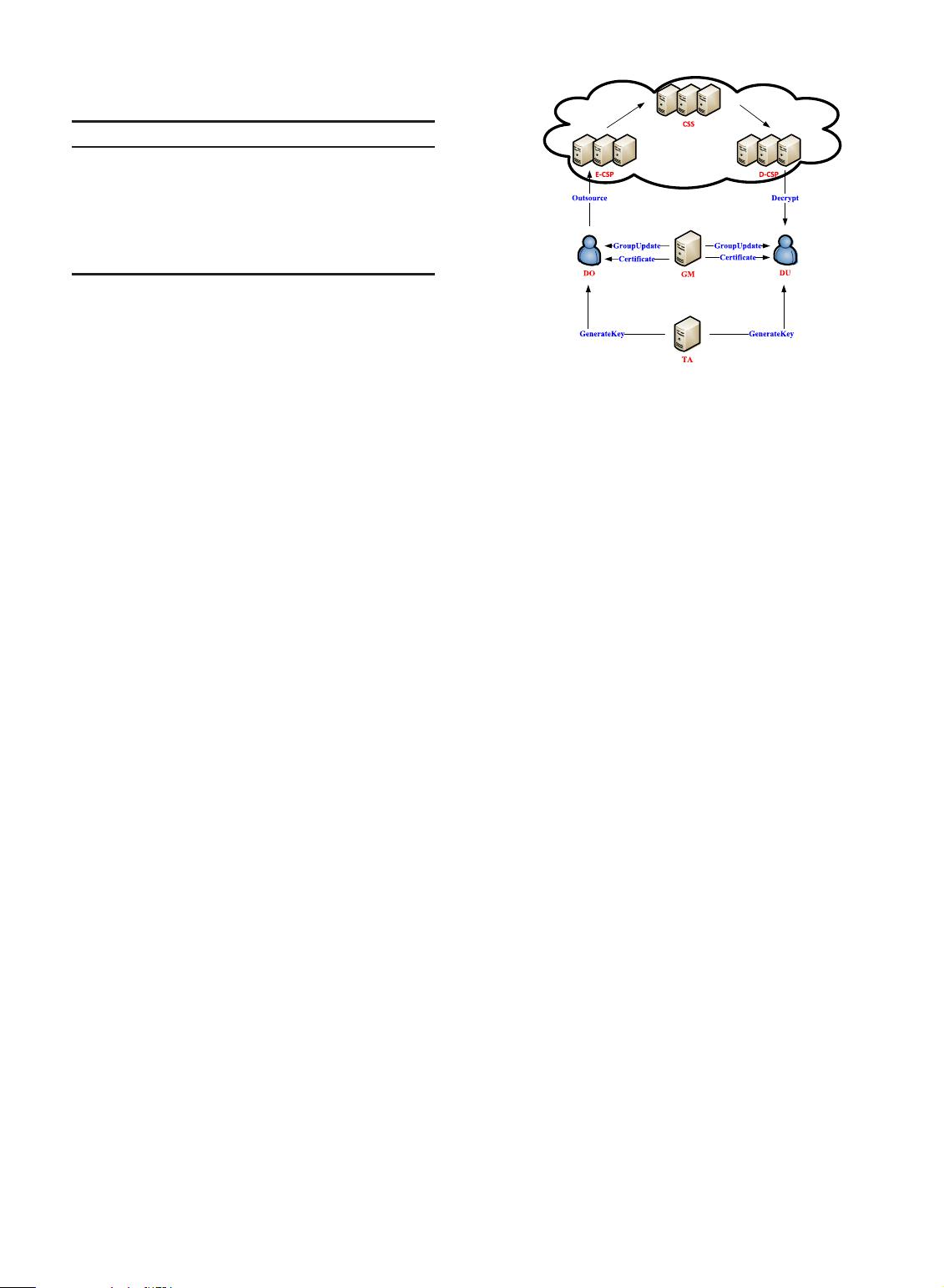
There are seven entities in total in our scheme. They are
listed in Table 1.
TA is a trusted authority who authenticates users’ attri-
bute sets and generates corresponding private keys for them.
GM is a trusted group manager who generates certificates
for users, updates the private keys of users, and applies CSS
for re-encryption operations. CSS in our scheme is a cloud
storage server, who is honest-but-curious. To reduce the
computation cost for cryptographic operations, we out-
source most of encryption operation to E-CSP and decryp-
tion operation to D-CSP. Users in the system play two roles:
data owner and data user. They are denoted as DO and DU
respectively. Our system model is shown in Fig. 2.
3.2 Algorithm Definition
In our CP-ABE scheme with user revocation, we assume
that a user’s private key includes two parts. One is associ-
ated with his authorized attributes and the other one is
associated with the group which he belongs to. When one
TABLE 1
Entities
Symbol Description
TA Trusted Authority
GM Trusted Group Manager
DO Data Owner
DU Data User
CSS Cloud Storage Server
E-CSP Encryption-Cloud Service Provider
D-CSP Decryption-Cloud Service Provider
Fig. 2. Our system model.
LI ET AL.: FLEXIBLE AND FINE-GRAINED ATTRIBUTE-BASED DATA STORAGE IN CLOUD COMPUTING 787









