牛顿迭代法详解：概念、MATLAB实现与收敛特性

牛顿迭代法是一种数值分析中的经典算法，用于寻找函数的零点，即求解非线性方程。该方法的核心思想是利用函数在某点附近的切线来逼近零点，通过不断迭代逼近精确解。以下将详细介绍牛顿迭代法的几个关键概念及其应用。 1. **基本概念**： - 牛顿迭代法基于泰勒级数展开，假设函数 \( f(x) \) 在点 \( x_n \) 的附近可以用一阶或二阶泰勒公式近似。初始时选择一个估计值 \( x_0 \)，然后通过构造函数 \( f(x) \) 在 \( x_n \) 处的切线，切线与x轴的交点作为下一个近似解 \( x_{n+1} \)。 2. **迭代公式**： - 迭代公式表达为：\( x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \)，其中 \( f'(x_n) \) 表示函数在 \( x_n \) 处的导数。当 \( f(x_{n+1}) \approx 0 \) 时，认为找到了方程的近似根。 3. **收敛性与速度**： - 牛顿迭代法在某些情况下具有快速的收敛性。如果函数 \( f(x) \) 在点 \( a \) 的邻域内二阶可导，并满足 \( f(a) \cdot f'(a) < 0 \)，那么根据牛顿法收敛定理，该方法将在 \( a \) 的某个邻域内收敛到 \( f(x) \) 的唯一实根。 - 收敛速度取决于函数的光滑程度和初始猜测点的选择，理想情况下，牛顿法的收敛速度比其他数值方法如二分法更快。 4. **MATLAB实现**： - MATLAB提供了内置函数如`fzero`或者自己编写循环来实现牛顿迭代法。例如，对于方程 \( f(x) = 0 \)，可以编写如下MATLAB代码： ```matlab function [xn] = newtonMethod(f, x0, tol, maxIter) xn = x0; for i = 1:maxIter if abs(f(xn)) < tol break; end xn = xn - f(xn) / f'(xn); end end ``` 这段代码定义了一个简单的牛顿迭代函数，输入方程函数 \( f \)，初始猜测 \( x_0 \)，允许的最大迭代次数和误差阈值。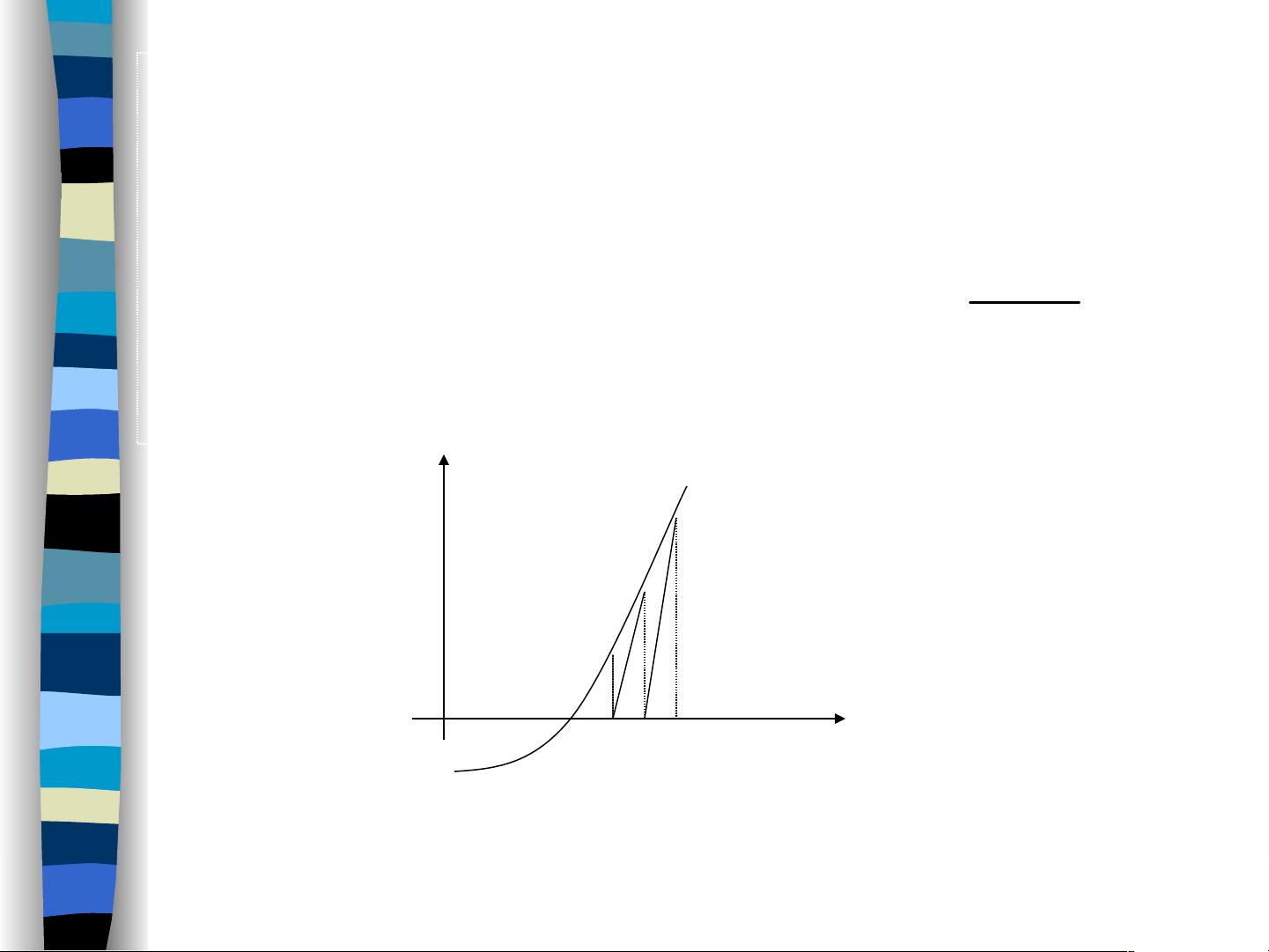 5. **几何解释**： - 从几何角度看，牛顿迭代法是寻找函数图形在当前估计点的切线与x轴的交点，这个交点就是下一次迭代的近似解。随着迭代的进行，每次迭代都会使函数值越来越接近零，从而逼近实际根。 6. **实验应用**： - 实验中使用牛顿迭代法求解给定的方程 \( f(x) + f'(x) + ... = 0 \)，要求达到的误差范围为 \( 10^{-3} \)。通过实际操作，学生可以体验到牛顿迭代法的执行过程和其在数值解算中的实用性。 牛顿迭代法是一种强大的数值求解工具，尤其适用于寻找函数的零点，其收敛性和速度取决于函数特性。在MATLAB等编程环境中，可以方便地实现这一方法，用于解决实际问题。在实际应用中，正确选择初始猜测和理解收敛条件至关重要。