"MATLAB多元非线性回归命令总结及应用"

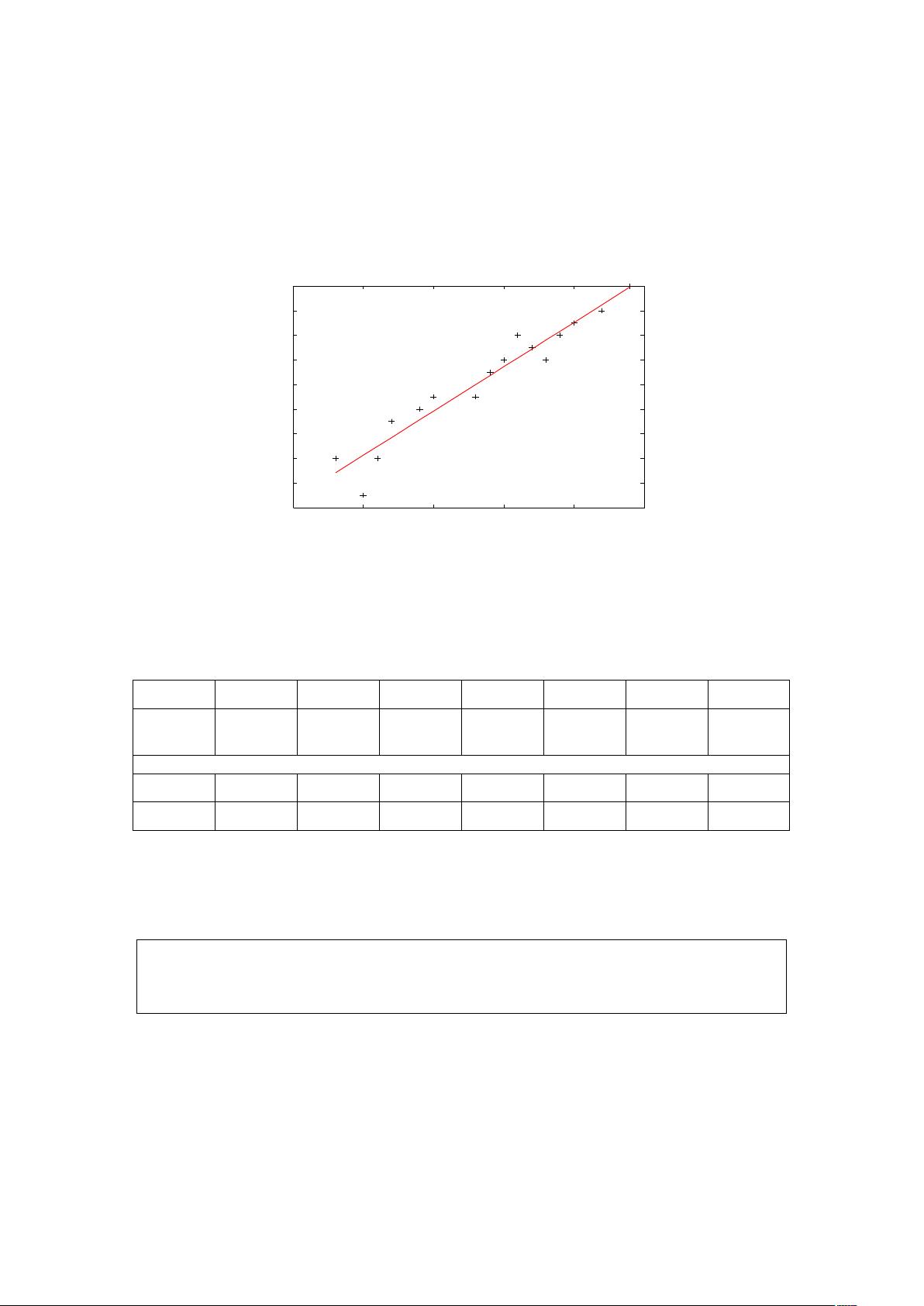
Matlab中的回归分析是一种数据分析方法，用于建立变量之间的关系模型。在Matlab中，有三条常用的回归命令，分别是polyfit(x,y,n)，regress(y,x)和nlinfit(x,y,’fun’,beta0)。这三条命令可以用于拟合不同形式的函数，并可以用于一元回归和多元回归分析。但由于拟合的近似结果没有唯一的标准答案，所以在同一个问题中使用这三条命令得到的结果可能会有所不同。 回归分析的操作步骤是根据实际数据点的图形，选择合适的函数形式，并提供该函数表达式的一般形式，其中包含待定系数。然后使用某条回归命令来求解所有的待定系数，这样就可以得到拟合结果。 一元多次拟合是回归分析中常用的方法之一，可以使用polyfit(x,y,n)命令进行拟合。这种方法适用于一元幂函数，即变量之间的关系为一元多次的多项式。一元回归是polyfit命令的简化版本，适用于一元线性回归模型。 多元回归分析是一种更加常用且通用性更高的方法，可以通过regress和nlinfit命令进行求解。多元线性回归模型是多元回归分析中常用的模型之一。这种方法可以适用于线性和非线性回归问题，并可以处理任意多个自变量。 在多元线性回归分析中，假设有n组观测值和p个自变量，可以建立模型 y=b0+b1x1+b2x2+...+bpxp ，其中 b0,b1,b2,...,bp 为待定系数。这种方法可以通过regress命令来求解。 对于多元非线性回归分析，可以使用nlinfit命令进行求解。这种方法适用于任何类型的函数，包括非线性函数，因此它具有最高的通用性。 综上所述，回归分析是一种建立变量之间关系模型的方法，可以通过Matlab中的polyfit、regress和nlinfit命令进行求解。在进行回归分析时，需要根据实际数据点的特征选择合适的函数形式，并确定待定系数的个数。由于拟合结果没有唯一的标准答案，因此使用不同的回归命令可能会得到不同的结果。对于多元回归问题，可以使用多元线性回归模型或多元非线性回归模型进行分析，具体方法根据实际问题的需求来确定。