"动态规划课程设计报告：戳气球问题与算法分析"

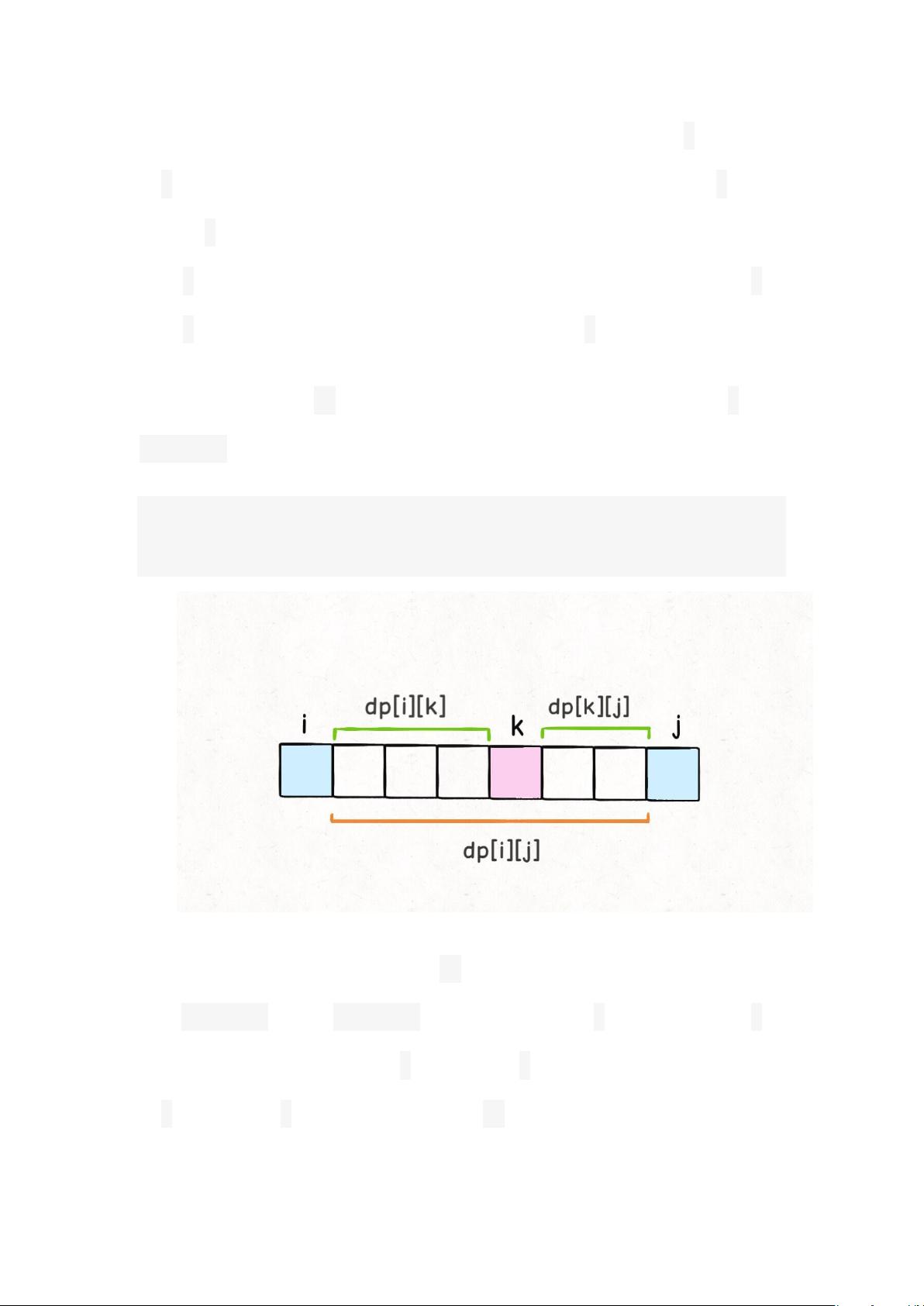
个数组拷贝到新的数组中，然后在新数组的两端插入1，这样原问题就转化为了戳气球的问题。接下来，我们就可以定义dp数组来解决问题。 三、分析子问题及其递推关系 定义dp数组dp[i][j]表示戳破气球i和气球j之间的所有气球能得到的最高分数。在i和j之间插入一个气球k（i<k<j），那么此时戳破气球k可得的分数为nums[i]*nums[k]*nums[j]，而此时dp[i][j]的值应该是dp[i][k]+dp[k][j]+nums[i]*nums[k]*nums[j]的最大值。因此，可以得到递推关系： dp[i][j] = max(dp[i][j], dp[i][k]+dp[k][j]+nums[i]*nums[k]*nums[j]) 四、确定dp数组的计算顺序 根据递推关系，可以得知dp[i][j]的计算依赖于dp[i][k]、dp[k][j]和nums[i]*nums[k]*nums[j]的值，因此dp数组的计算顺序应该是从长度较短的区间开始，逐步扩大区间长度，直至得到dp[0][n+1]的值。 五、复杂度分析 假设数组的长度为n，那么动态规划的过程中，需要计算每一个dp[i][j]。在计算dp[i][j]时，需要枚举i到j之间的每一个k，因此时间复杂度为O(n^3)。因此，整体的时间复杂度为O(n^3)。而在空间复杂度上，需要一个二维数组dp来存放中间状态，因此空间复杂度为O(n^2)。 六、具体实现代码 根据前面的分析，可以得到动态规划的具体实现代码如下： ```c int maxCoins(vector<int>& nums) { int n = nums.size(); vector<vector<int>> dp(n+2, vector<int>(n+2, 0)); vector<int> val(n+2, 1); for (int i = 1; i <= n; i++) { val[i] = nums[i-1]; } for (int len = 3; len <= n+2; len++) { for (int left = 0; left <= n+2-len; left++) { int right = left + len - 1; for (int k = left+1; k < right; k++) { dp[left][right] = max(dp[left][right], dp[left][k]+dp[k][right]+val[left]*val[k]*val[right]); } } } return dp[0][n+1]; } ``` 七、填表示例寻找最优解和最优方案 为了验证算法的正确性，可以用一些表示例来填表，找到最优解，以及对应的最优方案。 八、总结 通过本次戳气球的动态规划实验，我更加深入地理解了动态规划的思想和应用。在此过程中，我学会了如何对原问题进行调整，如何定义dp数组以及递推关系，以及如何确定dp数组的计算顺序。同时，我也了解了动态规划算法的时间复杂度和空间复杂度分析，在实现代码中也加强了对动态规划算法思想的理解。希望这次实验能够帮助我更好地理解算法设计与分析，从而对算法和数据结构有更深入的认识，也希望可以通过这次实验开启对于算法数据结构等方面的兴趣。希望学有所获，不至于大学四年一无所获。